Finding the critical point in quark-gluon plasma

Dam T. Son

Viewpoint

Finding the critical point in quark-gluon plasma

Institute for Nuclear Theory, University of Washington, Seattle, Washington 98103-1550, USA

January 20, 2009• Physics 2, 5

The critical point is one of the main features of the phase diagram of strongly interacting quark-gluon matter. Finding this critical point in the lab will require luck and an understanding of the possible experimental signatures.

Figure caption — **Figure 1:** A schematic QCD phase diagram. The solid blue line is the line of first-order phase transition. The broken blue line would be the line of second-order phase transition if $u$ and $d$ quarks were massless. The red dot is the critical point.

The study of critical points—the locations on a phase diagram where the boundary between phases disappears—has a very long history, starting with the observation of the critical point in water at the beginning of the 19th century. Recently, considerable attention has been paid to whether a critical point exists on the phase diagram of strongly interacting matter, which is known under various names as nuclear matter, quark matter, or quark-gluon plasma. One very important issue is whether the critical point can be found in experiments that involve colliding heavy nuclei. The most widely discussed signal of the critical point is the enhancement of fluctuations of final state observables, for example, the number of pions emitted in a collision. In a paper in Physical Review Letters [1], Mikhail Stephanov (University of Illinois at Chicago) points out new methods by which such fluctuations might be analyzed and eventually detected in experiments.

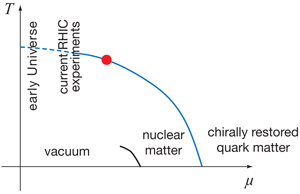
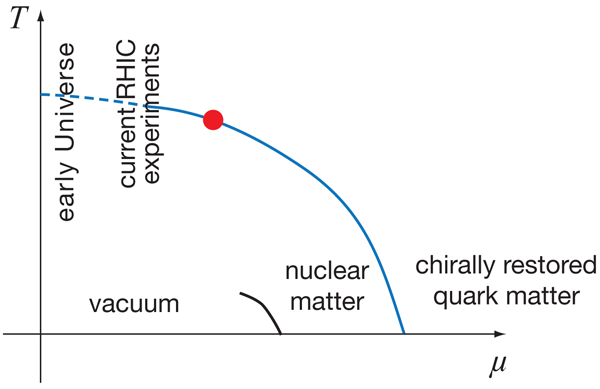
Without doubt, strong interactions are described by quantum chromodynamics (QCD). The phase diagram of QCD has two axes: the temperature $T$ and the chemical potential for quark number, $μ$ (see Fig.1 ). The chemical potential is directly related to the net quark density (i.e., the density of quarks minus density of antiquarks): at fixed temperature, larger $μ$ means larger net quark density. We can get the gross features of the QCD phase diagram by first setting either $μ$ or $T$ to zero. Imagine the early Universe when its temperature was much higher than the QCD scale, which is about $200 MeV$ . (The early Universe contains practically the same number of quarks and antiquarks, so $μ = 0$ .) At such high temperatures, we have a plasma of quarks and gluons, and the interaction between these particles is weak, thanks to asymptotic freedom (i.e., quarks are free to roam about when they are near each other but feel each other’s influence more and more strongly as they move farther apart).

As the Universe cools down, the interaction becomes strong and two things happen. The first is confinement: quarks and gluons are combined into hadrons (bound states of three quarks, or one quark and one antiquark). There does not have to be a phase transition associated with confinement alone (in a later state in the evolution of the Universe, electrons and protons would recombine into hydrogen without going through a true phase transition). The second phenomenon is spontaneous breaking of chiral symmetry. Under chiral symmetry, different types of quarks of left handedness (with spin pointing against the direction of motion) transform into each other, while independently right-handed quarks (spin pointing to the same direction as momentum) transform into each other. Chiral symmetry would be an exact symmetry of QCD if the quarks were massless. In the real world the $u$ and $d$ quarks (i.e., the two types of quarks that combine to form neutrons and protons) are not massless, but very light, so the chiral symmetry is not exact, but very good.

In the limit of massless quarks, there must be a phase transition related to chiral symmetry breaking. In the 1980s, Pisarski and Wilczek showed that if $u$ and $d$ quarks are the only relevant quarks, the phase transition can be second order [2]. Indeed, Monte Carlo simulations indicate that this phase transition is a second-order phase transition in QCD with two massless quarks. In the real world, the small masses of the $u$ and $d$ quarks smear this transition out into a rapid crossover. The temperature of the crossover is about $170 MeV$ .

Let us now stay on the other axis, at zero temperature, and increase the quark chemical potential (Fig. 1). One first jumps from vacuum to nuclear matter—the matter that makes up atomic nuclei. This jump is definitely a first-order phase transition. What happens at higher chemical potential, or densities, is less clear. It is rather well established that if $u$ and $d$ are the only relevant quarks, then at extremely high densities chiral symmetry should be restored. Therefore, there must be another, chiral, phase transition on the $μ$ axis. In contrast to the finite-temperature chiral phase transition, we have no reliable information about the location and the nature of this chiral phase transition. The problem is that at finite baryon densities all Monte Carlo algorithms suffer from the “fermion sign problem.” (In condensed-matter physics, the same problem also plagues the Hubbard model beyond half filling.)

As chiral symmetry is apparently broken in nuclear matter, the chiral phase transition should happen at a density higher than the nuclear matter density. A priori, such a transition can be either first order or second order. A second-order phase transition would be a quantum phase transition (since it happens at zero temperature). Most calculations, however, imply that the finite- $μ$ phase transition is first order [3]. One should be warned that these calculations rely on uncontrolled approximations to QCD.

If the finite- $μ$ chiral phase transition is indeed first order, then it should be first order also at small temperatures. But, as we mentioned above, there is just a crossover along the temperature axis. This means that there is a line of first-order phase transition, which has to terminate somewhere on the phase diagram. The point where the phase transition line terminates is a critical point, similar to the critical point of water. It should be emphasized that the existence of the critical point follows from one single assumption, that the finite- $μ$ chiral phase transition is first order.

The location of this critical point is completely unknown. As mentioned above, Monte Carlo methods suffer the fermion sign problem at finite quark chemical potential. This problem can be partially remedied when the chemical potential is not too large ( $μ / π T ≪ 1$ ) so if the critical point is located at small $μ$ one may have a chance to determine it. So far, however, lattice QCD calculations have failed to converge on a prediction for the location of the critical point.

Can one find the critical point experimentally? The only way one can achieve temperatures and densities relevant for strong interactions is to collide heavy nuclei, like the nuclei of gold (with atomic number $A = 197$ ). Such collisions are currently performed at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory. When two such nuclei are smashed together, a sequence of complicated processes occurs, but there are good indications that, for a brief time interval after the collision, one has a chunk of matter that behaves like a thermalized system, characterized by a temperature and a chemical potential. This tiny hot fireball expands, cools down, and eventually disintegrates into particles, tracing a trajectory on the phase diagram. With luck, one might be able to get this trajectory to pass close to the critical point.

If it does, how does one know? Some years ago, Stephanov, Rajagopal, and Shuryak discussed this issue in detail [4]. The idea is that near the critical point, the system has a “soft” mode, which is susceptible to external force. For example, in a magnetic system near the Curie point, the magnetic susceptibility $χ$ of an Ising ferromagnet diverges as a power of the correlation length $ξ$ as $χ \sim ξ^{2 - η}$ , where $η \approx 0.12$ . The susceptibility is not directly measurable in experiment, but is proportional to thermodynamic fluctuations, which are accessible experimentally. The signal of a critical point would be a nonmonotonic behavior of fluctuations. In the case of heavy-ion collisions one would see, for example, a bump in the fluctuations of the number of final state pions emitted in different collision events, $〈 (δ N)^{2} 〉$ .

In an ideal experiment, the correlation length would go to infinity and one would have a large enhancement of fluctuations near the critical point. In realistic heavy ion collisions, however, the size of correlation length is limited by the critical slowing down: as the system approaches the critical point, the relaxation time grows and at some point the system expands too quickly for thermal equilibrium to be maintained. The correlation length is frozen at the value where the expansion rate of the fireball is equal to the inverse relaxation time. By most estimates, the correlation length is quite modest, of order 2–3 $fm$ at its maximum. The magnitude of the variation of the fluctuations is limited by the size of the correlation length. Picking up such a variation may be possible, but there is worry that the magnitude of the signal is smaller than the theoretical estimate.

Instead of quadratic fluctuations $〈 (δ N)^{2} 〉$ , Stephanov has now considered the higher moments of the fluctuations, $〈 (δ N)^{3} 〉$ or $〈 (δ N)^{4} 〉$ [1]. Simple arguments show that statistical fluctuations become more and more non-Gaussian as one approaches the critical point, so the higher moments grow faster with the correlation length $ξ$ than the corresponding powers of quadratic fluctuations. For example, $〈 (δ N)^{3} 〉$ grows roughly as $ξ^{4.5}$ while $〈 (δ N)^{4} 〉$ roughly as $ξ^{7}$ . Thus these higher moments may be better signals to watch for in experiments.

Several experiments have been proposed to search for the critical point. The RHIC “energy scan” would run the current RHIC machine at about ten different center-of-mass energies ranging from $5 GeV$ per nucleon to about $60 GeV$ per nucleon. It is believed that at the current energy of $200 GeV$ per nucleon, RHIC explores the crossover region. There are also discussions about searching for the critical point at the older Super Proton Synchrotron (SPS) machine at CERN and at the future Facility for Antiproton and Ion Research (FAIR) in Germany. It is necessary to collide nuclei at different energies in order to explore the two-dimensional phase diagram: as a rule, raising the center-of-mass energy leads to a hotter plasma, but with smaller chemical potential. With luck, the critical point of QCD may lie in the region of the phase diagram accessible by experiments.

References

M. A. Stephanov, Phys. Rev. Lett. 102, 032301 (2009)
R. D. Pisarski and F. Wilczek, Phys. Rev. D 29, 338 (1984)
For example, M. Asakawa and K. Yazaki, Nucl. Phys. A 504, 668 (1989); J. Berges and K. Rajagopal, Nucl. Phys. B 538, 215 (1999)
M. A. Stephanov, K. Rajagopal, and E. V. Shuryak, Phys. Rev. Lett. 81, 4816 (1998); Phys. Rev. D 60, 114028 (1999)

About the Author

Dam Thanh Son received his Ph.D. at the Institute for Nuclear Research in Moscow in 1995. He was a postdoc at the University of Washington (1995–1997) and MIT (1997–1999). From 1999 to 2002 he was a professor at Columbia University and a RIKEN-BNL fellow. He moved to Seattle in 2002 when he became a Senior Fellow at the Institute for Nuclear Theory and a professor in the Physics Department, University of Washington. His research interests include QCD, applications of string theory, and many-body physics.