Spintronics without magnetism

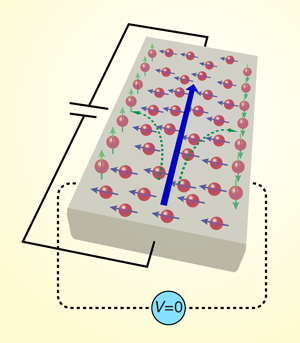
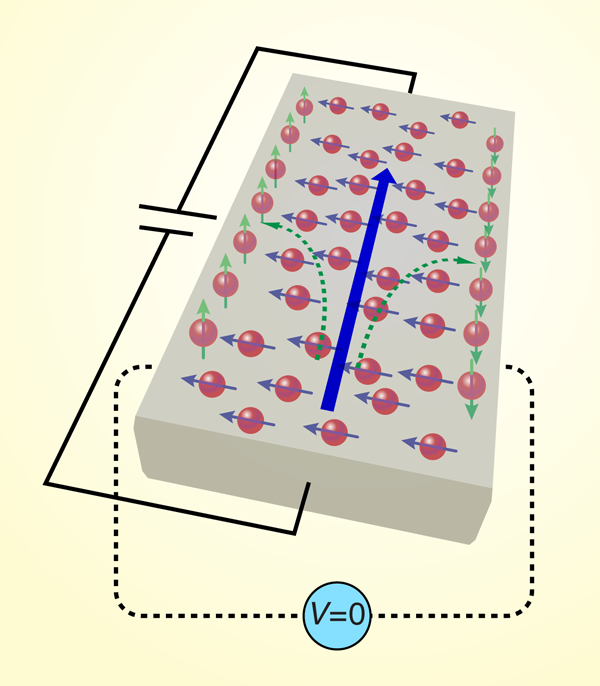
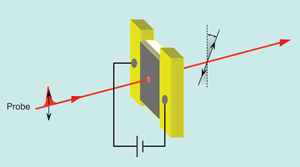
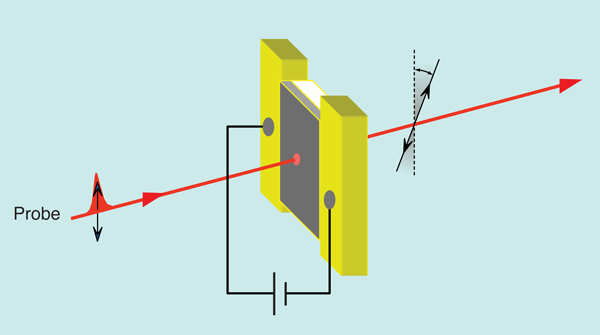
The spin Hall effect arises when a current flows through a semiconductor in the presence of a spin-orbit interaction, creating spin accumulation at the edges of a semiconductor transport channel (green arrows, Fig. 1). Though predicted over thirty years ago [12], unambiguous experimental evidence for the spin Hall effect required the development of high-sensitivity scanning optical imaging techniques capable of detecting small (microradians) Kerr rotation of reflected linearly polarized light (illustrated in Fig. 2) [7]. The technique has now been used to directly visualize the steady-state spin accumulation from the spin Hall effect of conduction-band electrons in several three-dimensional semiconductor crystals— $\text{GaAs}$ and $(\text{Ga,In})\text{As}$ [7] and $\text{ZnSe}$ [23]—as well as in $(\text{Ga,Al})\text{As}$ 2DEGs [24]. In addition, the optical nature of the measurement lends itself to spatiotemporally resolved pump-probe measurements that image the accumulation, precession, and decay dynamics near the channel boundary and provide insights into the dynamical evolution of the spin Hall effect (revealing, for instance, multiple time constants) [25].

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

Illustration: Alan Stonebraker

Illustration: Alan Stonebraker

×

The early experiments reporting the spin Hall effect ignited a surge of theoretical interest in the phenomenon, raising fundamental questions about its microscopic origins [26,27], the nature of spin currents [28,29], and the behavior of electrically generated spin accumulation in micron-scale devices [30,31]. The imaging experiments provide clear answers to some of these debates, demonstrating the clearly extrinsic nature of the spin Hall effect of electrons in all samples studied so far and also verifying the drift-diffusion dynamics of electrically generated spins in micron-scale devices [32,33]. When coupled with “Hanle measurements” that determine the precessional spin dephasing in an orthogonal magnetic field, the imaging experiments also provide a way to estimate the magnitude of the effect in terms of a “spin Hall conductivity.” Theoretical analysis of the extrinsic spin Hall effect in semiconductors using a spin-dependent Boltzmann approach provides good agreement with the experimentally measured spin Hall conductivity [33]. It is also apparent from both experimental measurements and theory that the spin Hall conductivity should depend both on the spin-orbit coupling parameter (characteristic of the semiconductor host band structure) and the gradient of the impurity scattering potential (in other words, the local electric field).

Nonetheless, key experimental observations still remain largely unanswered, for instance, although the extrinsic spin Hall effect in $\text{GaAs}$ is rapidly quenched with increasing temperature (observable up to about $150\text{K}$), experiments readily show the spin Hall effect at room temperature in $\text{ZnSe}$ despite the fact that the spin-orbit coupling parameter is much weaker in this material [23]. This temperature dependence is still a mystery that needs to be resolved. Further, the magnitude of the spin Hall effect in all the materials studied is still too small to envisage even proof-of-concept semiconductor devices that exploit the phenomenon and it is not clear what parameters could be manipulated for enhancing the signal. Addressing these questions provides an important challenge of both fundamental and technological implications.

As we mentioned above, the spin Hall effect is often accompanied by another spin polarization effect associated with a flowing charge current: bulk spin polarization generated by electron currents. As with the spin Hall effect, this effect in semiconductors with spin-orbit coupling was predicted decades before being confirmed by experiments [15,34]. Unlike the spin Hall effect, the spin polarization associated with this effect is larger, with a spatially uniform distribution and oriented in directions that depend on detailed device and crystal geometry (blue arrows, Fig. 1). This phenomenon has been called “current-induced spin polarization” and has also been observed in several semiconductors and geometries [9,23–25,35].

Current-induced spin polarization of conduction electrons was observed using Kerr rotation in strained semiconductors [9]. By studying the current-induced spin polarization in 2DEG devices fabricated along different crystalline directions for the current channel [25], we can disentangle contributions from “Rashba” and “Dresselhaus” fields (the distinction between the two is described in more detail below). Many of the experimental observations, such as the dependence of the spin polarization on the direction of the current density and electric field, can be understood as arising from these spin-orbit fields. However—as in the case of the spin Hall effect—we still do not have a sufficient understanding of the phenomenon that would provide guidelines for designing materials with favorable parameters. For instance, in contrast to $n$-type $\text{GaAs}$, current-induced spin polarization can be observed in $n$-type $\text{ZnSe}$ at room temperature [23]. The picture is further complicated by the poor correlation between the magnitude of current-induced spin polarization and the measured spin splittings in $\text{GaAs}$ [9] and competing proposals for spin-orbit mechanisms to describe this phenomenon [36]. These open theoretical questions combined with the potential utility of a spontaneous bulk electrically induced spin polarization present important outstanding challenges for spin-orbit physics in semiconductors.

So far, we have addressed the generation of spin polarization by a current. How can we manipulate the direction of this polarization once it has been created? The Rashba and Dresselhaus internal magnetic fields again come to our aid: the former originate in a spin-splitting in strained semiconductors that varies linearly with $k$, the crystal momentum, while the latter have a cubic dependence on crystal momentum. These $k$-dependent spin splittings act on spins in semiconductors as if they were “effective magnetic fields” that depend on the motion of charge in the material. Since similar spin splittings can be induced by strain in crystals, strain-engineered heterostructures provide a powerful means of systematically designing these internal magnetic fields, thus yielding means of using the spin-orbit coupling to manipulate spins. In analogy to real applied magnetic fields, strain-induced effective fields have been used for both coherent spin precession and electrically-driven spin resonance [8]. The internal magnetic field has been used for manipulating spin transport in $\text{GaAs}$, $\text{InGaAs}$, and $\text{ZnSe}$ devices [37,38]. Although the spin-orbit coupling parameter is much smaller in $\text{ZnSe}$ compared to $\text{GaAs}$, the spin-splitting energy scale is surprisingly comparable. The potential for all-electrical spintronics has been demonstrated in $\text{InGaAs}$ structures where precession of current-induced spin polarization is caused by strain-induced spin splittings, all in a single device without real magnetic fields or magnetic materials [36].

Finally, a very exciting development in recent years is the realization that one can engineer the interplay between the Rashba and Dresselhaus terms in 2DEGs, yielding spin polarization waves that survive over length scales substantially longer than predicted by diffusive dynamics alone. This phenomenon arises because the relationship between real-space trajectory and spin precession leads to a correlation between the electron’s position and its spin, resulting in an enhancement of the lifetime of certain spatially inhomogeneous spin polarization states beyond what would be expected for conventional spin diffusion—a spin helix. Recent optical transient spin-grating spectroscopy experiments [39] have probed the relaxation rates of spin polarization waves in $\text{GaAs}$ 2DEGs and shown that the spin polarization lifetime is maximal at a nonzero wave vector. This is contrary to expectations based on ordinary spin diffusion, but in quantitative agreement with recent theories that treat diffusion in the presence of spin-orbit coupling. Balancing the Rashba and Dresselhaus terms may enable modulation of the spin correlation length, with large dynamic range, through the application of external electric fields.

In summary, new pathways are emerging for exploiting the spin-orbit interaction to generate and manipulate carrier spin polarization in semiconductors. The wealth of experimental data gathered in recent years has clearly identified phenomena such as the spin Hall effect, current-induced spin polarization, and the spin helix [40] that could very well form the underpinnings of “spintronics without magnetism.” Bridging the chasm between fundamental understanding and a viable technology still remains a daunting challenge, but also offers stimulating scientific opportunities for quantum engineering at the very frontiers of condensed matter physics.