Catching relativity violations with atoms
Our best fundamental theories of gravity and particle physics share the core principle of local Lorentz symmetry, which encapsulates the laws of special relativity in modern language. In essence, this symmetry says that the laws of physics are the same for all (local) inertial observers moving through space, regardless of their velocity and orientation. There have been numerous experiments over the last decade, using light and known fundamental particles of the standard model, searching for violations of Lorentz symmetry [1]. So far, no convincing evidence for Lorentz violation has been found. However, should confirmed evidence of any type of Lorentz violation be found in the many ongoing experiments, the results would be profound and may provide the first experimental clue to the nature of Planck-scale physics.
Until recently, many effects of Lorentz violation in gravitational physics had not been explored. Writing in Physical Review D, Keng-Yeow Chung at the University of Singapore, Sheng-wey Chiow at Stanford University, US, Sven Herrmann at the University of Bremen, Germany, Steven Chu at the University of California, Berkeley, and the Lawrence Berkeley Laboratory, US, and Holger Müller at the University of California, Berkeley, report on the first experiment with atom interferometers acting as gravimeters that compares violations of Lorentz symmetry in gravity against those in electromagnetism [2]. They combine their results with lunar laser ranging analysis to establish the best existing laboratory constraints on eight of nine independent quantities that describe Lorentz violation for post-Newtonian gravity.
The recent interest in ever more sensitive tests of local Lorentz symmetry is primarily motivated by the possibility of uncovering experimental signatures from a fundamental theory that unifies general relativity and the standard model of particle physics. The basic idea is that minuscule violations of Lorentz symmetry could arise in candidate fundamental theories, such as field theories based on noncommutative geometry and quantum gravity theories like string theory. These ideas have been explored in a variety of recent works in the literature (for a review, see Ref. [3]).
To test Lorentz symmetry in a way that can be reproduced by many different experiments, it is very useful to have a standard against which results can be compared. A general framework for tests of Lorentz symmetry was developed in the 1990s and is called the standard-model extension [4]. In technical language, it is an effective field theory expansion. The standard-model extension incorporates the known physics of the standard model and general relativity while describing general Lorentz violation, for all known types of matter and fields, in terms of quantities called coefficients for Lorentz violation. These coefficients, which control the degree of Lorentz violation for a given type of particle or field, vanish when Lorentz symmetry holds exactly. The generality of the standard-model extension ensures that any proposed fundamental theory that causes Lorentz violation can be matched to various terms in the standard-model extension expansion.
Over the last decade, experiments with photons, electrons, protons, neutrons, neutrinos, and other particles have placed tight constraints on many of the coefficients for Lorentz violation in the standard-model extension [1]. There remain, however, many largely unexplored areas. Recently, the effects of Lorentz violation on gravity in the Solar System scenario were studied using a post-Newtonian formalism, which adds small corrections from curved spacetime to Newton’s law of gravity [5]. The post-Newtonian formalism for the standard-model extension was shown to have a partial overlap with the well-known parameterized post-Newtonian formalism [6], which describes deviations from general relativity in terms of ten parameters. The partial overlap indicates that new effects of Lorentz violation in gravity, described by the standard-model extension, remain unexplored.
The dominant effects in gravity are controlled by nine independent coefficients for Lorentz violation in the standard-model extension. Experiments capable of measuring these coefficients include lunar and satellite laser ranging, torsion pendulum tests, gyroscope experiments such as Gravity Probe B, classic tests of general relativity such as the perihelion shifts of the planets, and binary pulsar observations. Also, gravimeters can be used, which are among the experiments that can be carefully controlled in an Earth laboratory.
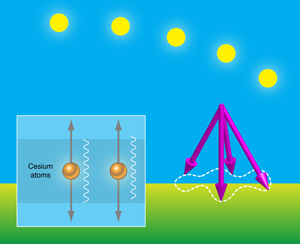
Gravimeters are devices that record changes in the local gravitational acceleration by measuring the motions of a test mass on the Earth’s surface (Fig. 1). Using gravimeters to test Lorentz invariance is an idea that surfaced more than three decades ago. In the 1970s, Will and Nordtvedt used gravimeter data to constrain Lorentz-violation parameters in the parameterized post-Newtonian expansion [7]. Analysis with superconducting gravimeters was carried out later by Warburton and Goodkind [8]. Nordtvedt also proposed gravimeter tests to look for additional anisotropies in gravity [9]. Motivated in part by results published by Alan Kostelecký and me [5], Müller et al. in a previous paper placed constraints on seven coefficients in the standard-model extension using atom interferometers as gravimeters [10].
The atom interferometer experiments, reanalyzed by Chung et al., use a novel Mach-Zehnder interferometer setup. The idea is to measure the phase difference between de Broglie waves of two sets of cesium atoms that have traveled along two different paths, using their quantum interference pattern (Fig. 1). In analogy with optical interference experiments, effective beam splitters and a mirror for the atoms are created by manipulating them with pulsed laser beams [11,12].
A vertical path for the cesium atoms is used, for which the measured phase difference for the two sets of atoms taking different paths is directly related to the value of the local gravitational acceleration. A hypothetical violation of Lorentz invariance in gravity produces daily and yearly sidereal time (that is, relative to the fixed stars rather than relative to the Sun’s position) dependences in the gravitational acceleration. In addition, since the atoms interact with laser pulses, the observable phase difference would also be affected by any Lorentz violation experienced by photons [13]. The experiment therefore actually compares the Lorentz symmetry of gravity with that of electromagnetism.
The data runs consisted of two 60-hour periods that were combined with data from a previous 10-day run [14]. From this data set, the team could search for variations in the local gravitational acceleration at six distinct frequencies. For example, two of the hypothetical signals vary at the Earth’s sidereal rotational frequency and twice this frequency. Significant systematic error sources in this experiment include the tidal effects from the Moon and Sun. An appropriate tidal model must therefore be used to subtract any tidal signals from the data before fitting the signal for Lorentz violation. Chung et al. improved upon previous analysis by modeling, in addition to the influences of the Moon and Sun, the effects of local tides, such as ocean loading.
By comparison, lunar laser ranging experiments, in which powerful laser beams are bounced from mirrors on the lunar surface, offer an orbital test of the Lorentz symmetry of gravity largely free from the effects of the Earth tides. Battat, Chandler, and Stubbs used over three decades of lunar laser ranging data to constrain five of the nine Lorentz violation coefficients for gravity [15]. Chung et al. combined their interferometer analysis with the lunar laser ranging results to tabulate the best constraints yet on gravity coefficients in the standard-model extension. The results show that five of nine possible coefficients are constrained to a value of zero to less than parts per billion, while another three of these nine coefficients are constrained at the level of parts per million.
The work by Chung et al. is among the first to establish experimental constraints on gravitational Lorentz violation in the standard-model extension in a carefully controlled laboratory setting. Improvements of their experiment for the future could involve trying to measure a time-varying horizontal component of the acceleration on the Earth’s surface due to Lorentz-violating effects. A novel configuration of an atom interferometer using, for example, atom-chip or atomic waveguides, should be capable of measuring these effects and could increase sensitivities to Lorentz violation in gravity. And such methods may be valuable in testing a new class of Lorentz-violating effects for protons, neutrons, and electrons, which reveal themselves only in gravitational experiments [16]. Compared to other types of Lorentz violation, these Lorentz-violating effects could be quite large and still have escaped detection so far. Atom interferometer experiments may be among the first experiments to explore these new effects.
References
- V. A. Kostelecký and N. Russell, arXiv:0801.0287
- K-Y. Chung, S-w. Chiow, S. Herrmann, S. Chu, and H. Müller, Phys. Rev. D 80, 016002 (2009); arXiv:0905.1929v2
- R. Bluhm, Lect. Notes Phys. 702, 191 (2006); arXiv:hep-ph/0506054
- V. A. Kostelecký, Phys. Rev. D 69, 105009 (2004)
- Q. G. Bailey and V. A. Kostelecký, Phys. Rev. D 74, 045001 (2006)
- C. M. Will, Theory and experiment in gravitational physics (Cambridge University Press, Cambridge, England, 1993)[Amazon][WorldCat]
- C. M. Will and K. Nordtvedt, Astrophys. J. 177, 775 (1972)
- R. J. Warburton and J. M. Goodkind, Astrophys. J. 208, 881 (1976)
- K. Nordtvedt, Phys. Rev. D 14, 1511 (1976)
- H. Müller et al., Phys. Rev. Lett. 100, 031101 (2008)
- M. Kasevich and S. Chu, Phys. Rev. Lett. 67, 181 (1991)
- S. Chu, Nature 416, 206 (2002)
- V. A. Kostelecký and M. Mewes, Phys. Rev. D 66, 056005 (2002)
- A. Peters, K. Y. Chung, and S. Chu, Nature 400, 849 (1999); Metrologia 38, 25 (2001)
- J. B. R. Battat, J. F. Chandler, and C. W. Stubbs, Phys. Rev. Lett. 99, 241103 (2007)
- V. A. Kostelecký and J. D. Tasson, Phys. Rev. Lett. 102, 010402 (2009)