Are iron pnictides new cuprates?

Zlatko Tesanovic

Viewpoint

Are iron pnictides new cuprates?

Institute for Quantum Matter and Department of Physics & Astronomy,The Johns Hopkins University, Baltimore, MD 21218, USA

July 13, 2009• Physics 2, 60

Are electronic correlations in the new iron-pnictide high-temperature superconductors as strong as in their older cuprate brethren? Yes, say some physicists; no, say others. X-ray experiments deliver the verdict.

Figure caption — **Figure 1:** An artist’s rendering of the hole ( $c$ ) and electron ( $d$ ) pockets on a $Fe$ -pnictide Fermi surface (FS). With moderately sized $U$ and $J_{Hund}$ found by Yang *et al.* [3] the main dynamical feature of $Fe$ pnictides is the nesting tendency between these pockets at wave vector $M = (π, π)$ . The particle-hole interband repulsion $W$ induces SDW while its particle-particle counterpart $G_{2}$ favors a $s_{\pm}$ interband superconductor. Such superconductor comes in two varieties: in the type-A case both $c$ and $d$ pockets are superconducting on their own, with $G_{2}$ providing an additional boost. The intrinsic type-B interband superconductivity is entirely due to $G_{2}$ and has only a single order parameter $Ψ$ , in contrast to the type-A.

Recent discovery of high-temperature superconductivity in iron-based compounds [1,2] has ignited a worldwide burst of activity. While experimentalists rushed to characterize the physical properties of these new materials and explore different avenues for further raising the temperature $T_{c}$ below which superconductivity occurs, the theoretical debate seemed to revolve around the similarities and differences between $Fe$ pnictides and twenty-odd year old cuprate high-temperature superconductors, still arguably the deepest mystery of condensed matter physics. Are electrons in $Fe$ pnictides as strongly correlated as cuprates, which—surely in their parent and lightly hole-doped states—evidently behave as Mott insulators? Or are they instead itinerant systems, with well-defined coherent bands and Coulomb interactions, which, while important, are well-screened and moderate in size? This is a fundamental question for this burgeoning field and in a recent article published in Physical Review B [3], Wanli Yang and colleagues at the Advanced Light Source at Lawrence Berkeley National Lab, in collaboration with several institutions in the US, Switzerland, Mexico, China, and the Netherlands report significant progress in settling this debate, by employing a combination of x-ray absorption (XAS) and resonant inelastic x-ray scattering (RIXS) techniques.

To be sure, there are important similarities between $Fe$ pnictides and cuprates. Both are layered systems, both have $d$ electrons playing a crucial role, and both feature close proximity of antiferromagnetic order and superconductivity in their respective phase diagrams. But there are crucial differences as well. Most importantly, the $d$ -electron count of $Fe$ versus $Cu$ is six (even) versus nine (odd). This has consequences: the parent state of a ${CuO}_{2}$ layer can be modeled by a single (hole) half-filled band and, by dictates of band-structure theory, should be a good metal. Instead, cuprates are anything but, as their parent state is turned into a Mott insulator—and Neel antiferromagnet—by strong short-range Coulomb repulsion $U$ , which penalizes putting two electrons (or holes in this case) on the same site making it impossible to move the charge around in a half-filled band.

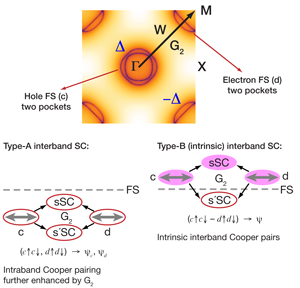
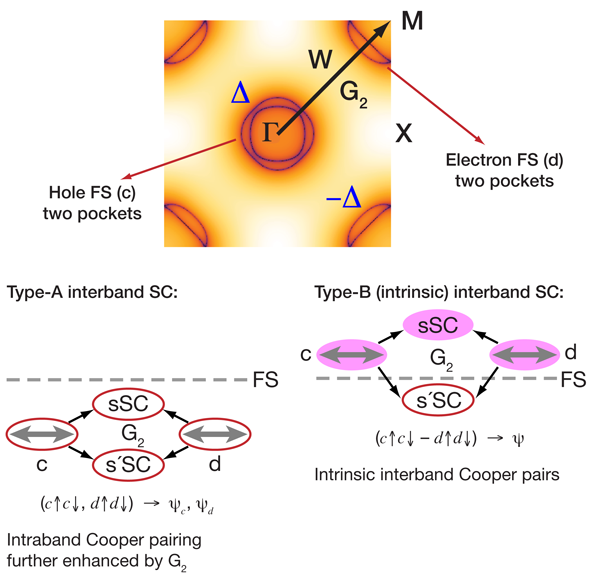
In contrast, having six $d$ electrons, or four $d$ holes in a filled $d$ shell, $Fe$ -pnictide layers demand a multiband description from the start. Furthermore, an even number of $d$ electrons implies that their band-structure-mandated fate is that of a semiconductor, or—if the top of the valence band crosses the bottom of the conduction band—a semimetal. Indeed, the parent $Fe$ pnictides are semimetals, with several electron and hole pockets on the Fermi surface [4], defined as the boundary between occupied and unoccupied states as a function of momentum. See Fig. 1 for an artist’s rendering of a typical Fermi surface of the $Fe$ pnictides. Such pockets are either nearly empty or filled, thereby mitigating the effect of $U$ since electrons/holes have more room to avoid each other than in the half-filled case. At this point, one can envision three scenarios: first, all $Fe$ $d$ electrons are localized by very large $U$ and the Hund’s rule reigns supreme. Hund’s coupling $J_{Hund}$ labors to align all the electrons’ spins and thus, by making the orbital wave function most antisymmetric, minimizes Coulomb repulsion at the atomic level. The result is a large local magnetic moment on $Fe$ sites, as six $d$ electrons line up into the maximal spin state $S = 2$ . The magnetism of such insulating $Fe$ -pnictide layers then sets in via various superexchange couplings and the small observed ordered moment stems from frustration among such couplings [5,6]. The second scenario is the opposite of the first: significant hybridization of $Fe$ 3 $d$ with pnictide $p$ orbitals and among themselves, which leads to an itinerant state, with coherent bands and significant metallic screening of $U$ , all the while rendering $J_{Hund}$ less important as the atomic limit gives way to covalency and enhanced itinerancy [7]. Finally, the third scenario is a “hybrid” of the previous two: some $d$ electrons are effectively localized while others are metallic, akin to heavy fermion systems [8]. There could still be a local moment but with a reduced spin, possibly $S = 1$ .

Now, Yang et al. enter the fray [3]. The authors’ clear ambition is to settle this debate and they appear to do so, by a combination of XAS and RIXS. The spectra they observe in $Fe$ pnictides exhibit considerable similarity to generic $Fe$ -based metals and point squarely to the itinerancy and metallicity of $d$ electrons. Furthermore, the said spectra show no relevant similarities to various $Fe$ -oxide insulators. Particularly worthwhile is the meticulous care with which Yang et al. analyze their experimental results in terms of their own theoretical calculations on $Fe$ -based clusters, employing powerful computational techniques like exact diagonalization and density functional theory. While their paper is comprehensive and data intensive, they still manage to keep the presentation pointed and elegant. They extract a moderate $U ≲ 2 eV$ —certainly comparable to a typical bandwidth—and considerably smaller $J_{Hund} \approx 0.8 eV$ , indicating a diminished inclination to form large local moments on $Fe$ sites.

Thus, the weight of evidence comes to the side of the second “itinerant” scenario, at least in the 1111 and 122 families of $Fe$ pnictides. The $d$ -electron itinerancy appears as the key ingredient of the physics and the accompanying banding and metallicity screen $U$ and reduce $J_{Hund}$ to the brink of irrelevance. Does this imply that the “localized” scenarios are out? Surely not. $U$ is still sizable and the strongly correlated starting point could be very useful in addressing certain problems, like the onset of local moment magnetism from within the metallic state, high measured resistivity, or the mysterious behavior of $Fe(Se,Te)$ [9]. Do the results of Yang et al. [3] imply that the basic outlines of the $Fe$ -pnictide physics are now all in place? A definite “yes and no.” A cautious “yes” now labels those theoretical approaches that start from the metallic side and use the nesting proclivities of the hole and electron pockets to incorporate the effects of moderate correlations [7,10,11]. In such theories, the parent compound has an itinerant $(π, π)$ spin-density wave (SDW) with inherently small ordered moment.

A more pesimistic “no,” however, is the answer when it comes to the superconductivity itself. While the itinerant picture offers an attractive route to the purely electronic superconductivity, via the enhancement of the interband pair repulsion near a SDW [7,10–12], there is a catch: the natural outcome of this approach is the so-called $s_{\pm}$ state [12], with the superconducting gap that switches sign between hole and electron portions of the Fermi surface (see Fig. 1). Nonetheless, the overall symmetry is still an $s$ wave and the $s_{\pm}$ state cannot avoid the intraband repulsion. Can the interband pairing overcome this repulsion and produce a high- $T_{c}$ $s_{\pm}$ state under certain favorable circumstances? Could phonons help by reducing the intraband repulsion? Is the interband superconductivity type A or B (see Fig. 1)? Is there an unambiguous experimental signature of the $s_{\pm}$ state? These and other, yet to be formulated questions will keep the iron-based high-temperature superconductors on the research frontier for a long while.

Acknowledgments

Work at the Johns Hopkins-Princeton Institute for Quantum Matter was supported by the U.S. Department of Energy Office of Science under Contract No. DE-FG02-08ER46544.

References

Y. Kamihara et al., J. Am. Chem. Soc. 130, 3296 (2008)
X. H. Chen et al., Nature 453, 761 (2008)
W. L. Yang et al., Phys. Rev. B 80, 014508 (2009)
H. Ding et al., Europhys. Lett. 83, 47001 (2008)
Q. Si and E. Abrahams, Phys. Rev. Lett. 101, 076401 (2008)
T. Yildirim, Phys. Rev. Lett., 101, 057010 (2008)
V. Cvetkovic and Z. Tesanovic, Europhys. Lett. 85, 37002 (2009)
J. Wu, P. Phillips, and A. H. Castro-Neto, Phys. Rev. Lett. 101, 126401 (2008)
Y. Xia, D. Qian, L. Wray, D. Hsieh, G. F. Chen, J. L. Luo, N. L. Wang, and M. Z. Hasan, Phys. Rev. Lett. 103, 037002 (2009); For additional background, see A. V. Balatsky and D. Parker, Physics 2, 59 (2009)
A. V. Chubukov, D. V. Efremov, and I. Eremin, Phys. Rev. B 78, 134512 (2008)
Y. Ran, F. Wang, H. Zhai, A. Vishwanath, and D. H. Lee, Phys. Rev. B 79, 014505 (2009)
I. I. Mazin, D. J. Singh, M. D. Johannes, and M. H. Du, Phys. Rev. Lett. 101, 057003 (2008)

About the Author

Zlatko Tesanovic is a Professor of Physics at The Johns Hopkins University in Baltimore, MD. His research interests are in theoretical condensed matter physics, revolving primarily around high temperature superconductors and related materials, quantum Hall effects, and other manifestations of strong correlations and emergent behavior in quantum many-particle systems.

Evidence for weak electronic correlations in iron pnictides

W. L. Yang, A. P. Sorini, C-C. Chen, B. Moritz, W.-S. Lee, F. Vernay, P. Olalde-Velasco, J. D. Denlinger, B. Delley, J.-H. Chu, J. G. Analytis, I. R. Fisher, Z. A. Ren, J. Yang, W. Lu, Z. X. Zhao, J. van den Brink, Z. Hussain, Z.-X. Shen, and T. P. Devereaux

Phys. Rev. B 80, 014508 (2009)

Published July 13, 2009

Read PDF