Good fortune from a broken mirror

Klaus Jungmann

Viewpoint

Good fortune from a broken mirror

Kernfysisch Versneller Instituut, University of Groningen, 9747 AA Groningen, The Netherlands

August 10, 2009• Physics 2, 68

A huge, predicted atomic parity violation has now been observed in ytterbium, further aiding tabletop experimental searches for physics beyond the standard model that complement ongoing efforts at high-energy colliders.

Figure caption — **Figure 1:** Electrons in an atom interact with the nucleus through the electromagnetic force via the exchange of massless photons ( $γ$ ). The weak force is mediated by $Z^{0}$ bosons. The weak effects by themselves are too small to see directly. However, it is possible to measure the effect of $Z^{0}$ boson exchange between an electron and a neutron by looking at the quantum mechanical interference between this process (right) and the electromagnetic interaction (left). The figure provides a pictorial representation of how the quantum interference between the two processes—the sum of the amplitudes squared—contributes to a measureable signal.

The Berkeley group performed laser measurements to determine how the weak force, which very slightly modifies the interactions between the electrons and the nucleus, affects the ground state of an $Yb$ atom. Since the weak interaction effect is much smaller than the Coulomb interaction between the electrons and the positively charged nucleus, a tour de force in experimental efforts is required to extract it from the transition rate between the ground state and an excited state. Tsigutkin et al.s experimental success is based on careful quantum mechanical interference techniques and their ability to thoroughly control systematic effects that could otherwise mimic a signal. But to fully appreciate the Berkeley group’s experimental art, some background is first required.

The standard model of particle physics describes every known electromagnetic, weak, or strong process in nature in one coherent picture over the entire energy range that is currently accessible by experiment [1]. We know that matter consists of fundamental fermions: the leptons such as the electron, and the quarks, which form hadrons such as protons and neutrons. The forces between the matter particles are mediated through the exchange of “gauge” bosons. These are the massless photons $γ$ for electromagnetism, massive $Z^{0}$ , $W^{+}$ , and $W^{-}$ bosons for weak processes, and eight gluons for the strong interaction.

The weak force is special because it does not respect certain discrete symmetries. These include the parity ( $P$ ) (or, the mirror symmetry), which describes the symmetry between right- and left-handed particles; charge conjugation ( $C$ ), which is the exchange of particles by antiparticles, i.e., particles with the same mass but opposite charge; and the combination of these two symmetries ( $C P$ ). Scientists first observed parity violation in 1957 with a crucial pioneering experiment on the $β$ -decay of polarized $^{60} Co$ nuclei [5] where it was found that electrons are emitted preferentially in the direction of the nuclear spin. The standard model explains this process by assuming that the $W^{\pm}$ bosons that govern the weak interaction only exist in a left-handed version.

One outgrowth of the standard model is that the electromagnetic and weak interactions are really just different manifestations of one single electroweak force. This unification led to the prediction of another neutral boson called the $Z^{0}$ , which was observed in both high-energy neutrino scattering experiments [6] and at low energies in atoms. The discovery of $Z^{0}$ removed any doubts about the general correctness of the theory [7] and became a crucial success of the standard model. The $Z^{0}$ boson exchange in atoms between electrons and nuclei is associated with parity violation and manifests itself, for example, by different absorption of left- and right-circularly polarized light [3].

The virtual particles that carry the electroweak force can exist only for a short time $Δ t$ , given by the energy corresponding to their mass $m_{X}$ and the Heisenberg uncertainty relation. This gives them a range $r_{X} = c Δ t \approx ħ / (m_{X} c$ ), which for photons is infinite, but for weak bosons is only 1/1000 of the diameter of a proton or neutron. As a consequence, the weak effects in atoms are very small and only affect those electrons with wave functions that overlap with the nucleus, such as the ground state in $Yb$ . Since the weak effects are so small, we can fairly accurately calculate the electronic energy levels in atoms using only parity conserving electromagnetic interactions and a purely electromagnetic Hamiltonian describing the Coulomb interaction between electrons and the nucleus, which is mediated by $γ$ exchange. The additional small contribution from $Z^{0}$ boson exchange can be treated as a perturbation that mixes wave functions of different parity, i.e., the true energy levels in the atom correspond to mixtures of different parity electromagnetic states [8]. Now, the closer states of opposite parity are to each other in energy, the larger their mixing will be. In this respect, nature has bequeathed $Yb$ with a favorable atomic structure in which weak effects are actually quite large [9]. In addition, in the standard model the strength of weak interactions is characterized by a quantity called the weak charge $Q_{W}$ , which is determined primarily by the number of neutrons in the nucleus (the protons play only a minor role). The size of parity violation effects in atoms also scales approximately with $Z^{3}$ , which favors observing such effects in heavy atoms, like $Yb$ [8], or heavier.

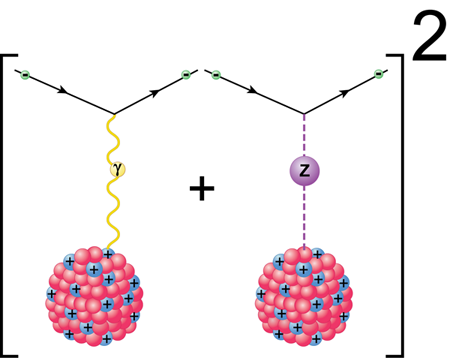
The experimental challenge in the $Yb$ atom experiment performed by the Berkeley group is to make the tiny parity violating effect visible. For that, the authors have chosen to laser excite the “forbidden” transition $^{1} S_{0}$ ( $6 s^{2}$ ) to $^{3} D_{1}$ ( $5 d 6 s$ ) at $408$ - $nm$ wavelength. Because $Z^{0}$ boson exchange mixes the $^{3} D_{1}$ state with the $^{1} P_{1}$ ( $6 s 6 p$ ) state, there is a tiny transition amplitude $ζ$ for this otherwise forbidden transition. This amplitude would provide a measure of the weak interaction, but it cannot be measured directly. The trick therefore is to place the $Yb$ atoms in a combination of static magnetic and electric fields [2,4]. The magnetic field splits the magnetic sublevels in the excited state (the Zeeman effect). The electric field $E$ also mixes atomic states of opposite parity (the Stark effect), which interferes with the parity mixing in the atom and yields a strong enhancement of the overall observable effect. In particular, two terms arise in the transition rate $R$ between the ground state and individual Zeeman levels. One of them is determined by the Stark effect only and is proportional to $E^{2}$ and the second one (represented pictorially in Fig. 1) comes from the interference between the Stark effect and the weak interaction and is proportional to $ζ \cdot E$ . Hence $R \propto a E^{2}$ $+ b ζ \cdot E$ , where the constants $a$ and $b$ depend on the states involved in the transition and the light polarization and intensity. To separate out the second, much smaller term, the Berkeley group modulates the electric field at a frequency $Ω_{M}$ . The transition rates then contain a part that depends on $ζ$ and oscillates at $Ω_{M}$ and another part that oscillates at $2 Ω_{M}$ . With a modulation phase and frequency sensitive detection (lock-in) method they were able to produce a signal at $Ω_{M}$ , from which the parity violation amplitude can be extracted, on top of a background that is some 25 times larger that the signal itself.

The measurement at Berkeley demonstrates that it is possible to observe parity violating effects in complicated atoms such as $Yb$ . This is an exciting result, because there are seven stable isotopes of $Yb$ . The strong dependence of the weak charge on the neutron number means it will be possible to study the effect of nuclear neutron distributions on the weak interaction in $Yb$ [10]. The so-called anapole moments, which reflect the parity violating interaction between a single (valence) nucleon and the core of an atomic nucleus [11], can be accessed by looking at different hyperfine components in isotopes with odd neutron number. These experiments are very sensitive to small perturbations and systematic errors, but the Berkeley group shows that with time they should be able to minimize these problems.

The Ytterbium experiment can potentially go further than verifying physics within the standard model—it may permit future sensitive searches for new physics beyond the standard model. It’s not surprising that the theory may need to be extended, given that that there are still many open questions, among them why there are exactly six leptons and six quarks, and which mechanisms underlie certain symmetry breakings.

Beyond $Yb$ , there are a number of complementary experiments on their way that use isotopes of the alkali atom francium ( $Fr$ ) [12] or of the alkali-like barium ion ( ${Ba}^{+}$ ) [13] and radium ion ( ${Ra}^{+}$ ) [14]. (The theoretically predicted enhancement factors of weak effects in these atoms compared to $Cs$ are 2.3, 16, and 52.) The atomic structure of these two atoms is simpler and easier to calculate than that of $Yb$ . The combination of advanced calculations and these precision experiments will allow us to determine the weak charge $Q_{W}$ to much better than $1 %$ accuracy. Together, these atomic parity violation experiments has the great potential to reveal new physics such as a new weak boson $Z^{0'}$ , supersymmetric particles, leptoquarks, or smaller components making up the matter building fundamental fermions, all of which would cause a modification of the weak charge and the Weinberg angle (a free parameter in the equation that determines the strength of the weak interaction) [12–16]. Alternatively they can provide important limits on parameters in such models, which have been suggested to extend the standard model, and thereby steer theoretical model building—just as cutting edge experiments in $Cs$ and its subsequent theoretical exploitation continue to do [16].

More than 50 years after the discovery of mirror symmetry breaking in physics, the subject remains lively and has a robust chance to provide new surprises. The large weak effects in heavy atoms, such as what the Berkeley group has demonstrated in $Yb$ , open a new round for exploiting the broken mirror symmetry and shine new light on the yet not-understood features of the standard model.

References

S. L. Glashow, Nucl. Phys. 22, 579 (1961); S. Weinberg, Phys. Rev. Lett. 19, 1264 (1967); A. Salam, in Elementary particle theory: relativistic groups and analyticity, Proceedings of the 8th Nobel Symposium, edited by N. Svartholm (Almquist and Wicksell, Stockholm, 1968); G. t’Hooft, Nucl. Phys. B33, 173 (1971); G’Hooft and M. Veltmann, Nucl. Phys. B44, 189 (1972)
K. Tsigutkin, D. Dounas-Frazer, A. Family, J. E. Stalnaker, V. V. Yashchuk, and D. Budker, Phys. Rev. Lett. 103, 071601 (2009)
M. A. Bouchiat et al., Phys. Lett. 117B, 358 (1982)
C. S. Wood et al., Science 275, 1759 (1997)
C. S. Wu, Phys. Rev. 105, 1413 (1957)
F. J. Hasert et al., Phys. Lett. 46B, 121 (1973)
S. Weinberg, Dreams of a Final Theory (Pantheon Books, New York, 1992)[Amazon][WorldCat]
P. G. H. Sandars, Phys. Scr. 36, 904 (1987); M. A. Bouchiat and C. Bouchiat, in Parity Violation in Atoms and Polarized Electron Scattering, edited by B. Frois and M. A. Bouchiat (World Scientific, Singapore, 1999)[Amazon][WorldCat]; V. F. Dmitriev and I. B. Khriplovich, Phys. Rep. 391, 243 (2004); J. S. M. Ginges and V. V. Flambaum, 397, 61 (2004)
V. A. Dzuba et al., Z. Phys. D 1, 243(1986); D. DeMille, Phys. Rev. Lett. 74, 4165 (1995)
B. A. Brown et al., Phys. Rev. C 79, 035501 (2009)
W. C. Haxton and C. E. Wieman, Annu. Rev. Nucl. Part. Sci. 51, 261 (2001)
G. Gwinner et al., Hyperfine Interact. 172, 45 (2006); G. Stancari et al., Eur. Phys. J. Special Topics 150, 389 (2007)
J. A. Sherman et al., Phys. Rev. A 78, 052514 (2008)
L. W. Wansbeek et al., Phys. Rev. A 78, 050501 (2008); B. K. Sahoo et al., Phys. Rev. A 79, 052512 (2009); K. Jungmann, Hyperfine Interact. 171, 41 (2006); R. Pal et al., Phys. Rev. A 79, 062505
M. J. Ramsey-Musolf, Phys. Rev. C 60, 015501 (1999)
S. G. Porsev et al., Phys. Rev. Lett. 102, 181601 (2009)

About the Author

Klaus Jungmann studied physics at the University of Heidelberg, Germany, and was later a post-doctoral researcher at IBM Almaden Research Center in San Jose, California. He is currently a full professor at the University of Groningen and director of the Kernfysisch Versneller Institute, which oversees a dedicated facility (TRI $μ$ P) for research on fundamental interactions and symmetries at low energies. His research interests lie at the interface between atomic, particle, and nuclear physics in precision experiments. This includes the determination of fundamental constants and searches for new physics with free muons and the muonium atom.