Cosmic alchemy in the laboratory

Michael Wiescher

Trend

Cosmic alchemy in the laboratory

University of Notre Dame, Department of Physics & Joint Institute of Nuclear Astrophysics, Notre Dame, IN 46556, USA

August 17, 2009• Physics 2, 69

Advances in experimental techniques that measure nuclear reactions that occur in stars are opening new opportunities for understanding the stellar and chemical evolution of our Universe.

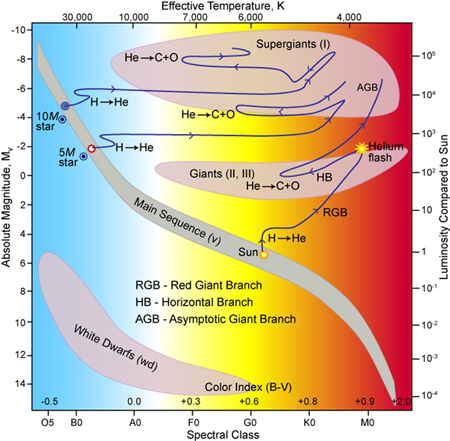
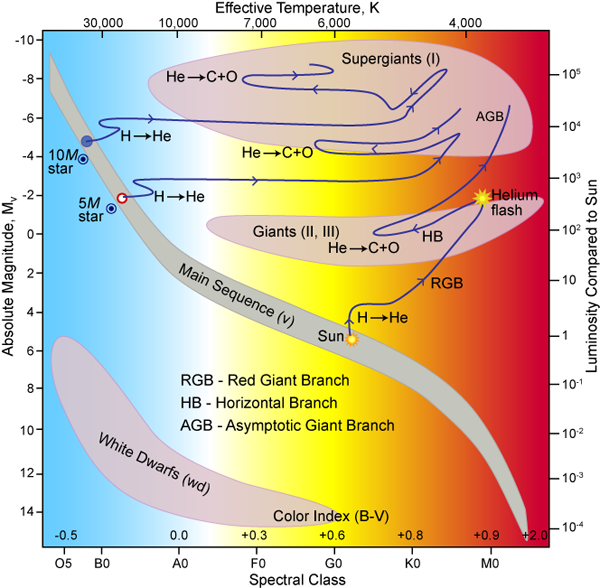
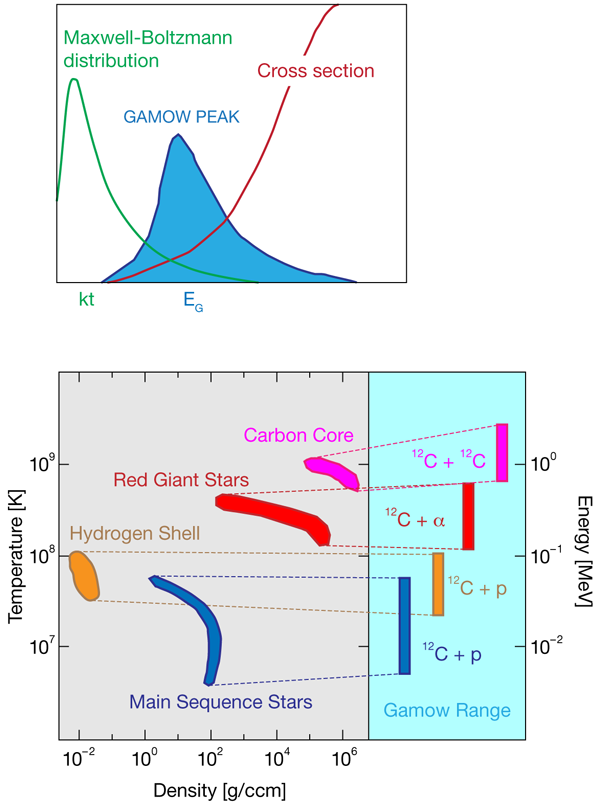
Far from being eternal lights in the sky, stars are dynamic objects each with a life cycle that depends on their mass and internal composition. Stars evolve as protostars by gravitational contraction of a molecular cloud until the increasing core temperature and density triggers the ignition of hydrogen burning. At this state the stars reach their “main sequence position” in the Hertzsprung-Russell diagram used by astrophysicists (Fig. 1). Hydrogen burning converts four hydrogen nuclei to one helium nucleus, and the released nuclear energy stabilizes the stellar core against further gravitational contraction until the hydrogen fuel is used up. The core starts contracting again until the ignition of helium burning, which converts three helium nuclei into one carbon nucleus. As the core burns, the temperature in the surrounding layers increases, causing the star to burn hydrogen in these shell layers and expand. This changes its surface temperature and the star joins the family of red giants following the trajectory shown in Fig. 1. As the star burns helium, the energy generated stabilizes the star against gravitational contraction until the helium fuel declines. Low-mass stars do not get beyond helium burning because the gravitation is not sufficient to trigger the possible subsequent carbon burning phase; they end up as white dwarfs, which are composed of carbon and oxygen. More massive stars develop a carbon-burning core with helium and hydrogen-burning shells after the depletion of the helium fuel.

Figure caption — **Figure 1:** Astrophysicists categorize star types and stellar evolution scenarios using the Hertzsprung-Russell diagram, which organizes stars in terms of their luminosity (which is related to their mass and size) and color (surface temperature). The blue lines show three different evolutionary scenarios for stars of 1 solar mass, 5 solar masses, and 10 solar masses as they move from hydrogen burning, to helium burning, and beyond.

In this way stars evolve though various phases and move along a rather complex trajectory in the Hertzsprung-Russell diagram that primarily depends on the original stellar mass and its core composition. For very massive stars—larger than eight solar masses, carbon burning is followed by a number of subsequent short burning phases—neon, oxygen, silicon burning—which convert the core material to iron and nickel. No further fusion processes can generate energy, so electron capture on iron and nickel isotopes destabilize the core, which collapses under the gravitational force, triggering a supernova explosion. The corresponding evolutionary phases are driven by nuclear reactions within the star, providing both the energy to resist gravitational collapse and the fuel to power nucleosynthesis of the chemical elements.

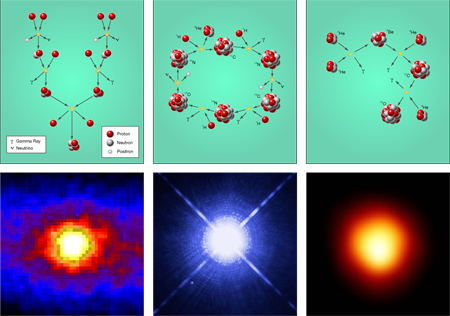
Multiple nuclear reactions occur in every burning stage of stellar life, but in most cases only a few reactions turn out to be critical in determining the major phases of the burning process (Fig. 2). When stars burn hydrogen and helium, the critical reactions are mostly radiative proton and alpha capture processes, whereas during the subsequent carbon and oxygen burning phases, the key processes are predominately nuclear fusion reactions. The reaction rates of these processes not only determine the evolution of elements through nucleosynthesis but also the energy production and timescale for each of the consecutive stellar burning phases.

At stellar temperatures, the reaction rates are extremely low, which is why the lifetimes of stars are counted in millions of years. Over the past several decades, considerable experimental and theoretical effort has been spent analyzing and understanding these critical low-energy reaction processes in stars. The extremely low cross sections limit the direct measurement of the reactions at energies corresponding to the stellar temperature. This is mainly because the rate of reaction signals in the detectors is extremely low, while the background noise is large. This deleterious background is caused by cosmic-ray-induced radiation in the detectors, natural radiation from the experimental environment, and beam-induced background from light (low atomic number) target impurities. What we know about the reaction rates that occur in a burning star at low energies therefore comes from extrapolations of experimental cross sections, measured at energies that are substantially above the stellar energies. The accuracy of our computational models of stellar evolution and nucleosynthesis depends critically on how well we understand and how reliably we extrapolate low-energy nuclear reaction cross sections.

The Gamow window

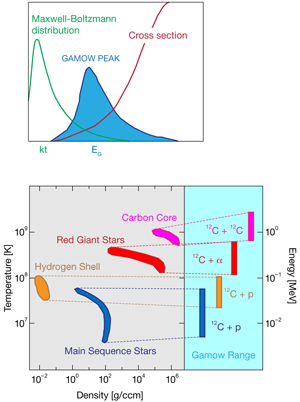
The characteristic energy range for any reaction in a stellar burning phase happens where the Maxwell Boltzmann distribution for the interacting particles overlaps with the low-energy tail of the reaction cross section (Fig. 3)—the so-called Gamow window [1]. The energies at which this overlap occurs depend on the charge $Z$ of the interacting nuclei and the temperature of the environment and they have to be calculated for each specific reaction. The Gamow energies are between $3 keV$ and $30 keV$ for typical stellar hydrogen-burning reactions in the cores of main sequence stars, around $300 keV$ for stellar helium-burning reactions such as occur in the cores of red giant stars, and in the range of $1 MeV$ to $2 MeV$ for stellar carbon burning, as demonstrated in Fig. 3.

New experimental techniques have been developed over the last few years, which for the first time have allowed the direct study of nuclear reactions near or even at stellar energies. In particular, researchers have built underground accelerator laboratories where thousands of meters of rock shield cosmic rays and reduce the background on the detectors. Alternatively, researchers have designed complex radiation detector arrays that actively reject background radiation by discriminating events on the basis of timing and energy determination. The utilization of inverse kinematics techniques introduces another method to optimize the experimental conditions at low energies. This approach is based on the development of an intense heavy ion beam bombarding a light nuclei gas target. Because of the momentum transfer in the reaction, the products move forward with the beam and can be collected and counted with high efficiency after being separated from the heavy ion beam projectiles by recoil separators with high momentum selectivity.

Despite these improvements in background reduction, the fact remains that the actual cross sections at stellar burning conditions are extremely small and in many cases below the limits of detectability. The experiments are therefore greatly helped by new theoretical techniques for extrapolating these experimental data more reliably into the Gamow range. These techniques rely on a better understanding of the nuclear structure of the compound nuclei as well as on a more reliable theoretical treatment of the reaction mechanisms and the interference between the various reactions channels. A number of “indirect” experimental techniques [2,3] have added substantially to the ability to identify and discriminate among the low-energy reaction contributions.

The key nuclear reactions that keep stars burning

In low mass stars ( $M \leq 1.5 M_{sun}$ , where $M_{sun}$ is the mass of the sun, about $2 x 10^{30} kg$ ) hydrogen burning is driven by a proton-proton ( $p p$ ) chain reaction (Fig. 2, left). Ultimately the $^{1} H + p \to e^{-} + ν +^{2} H$ fusion reaction determines the timescale of the overall conversion process of four $^{1} H$ isotopes to one $^{4} He$ isotope, and the extremely low cross section of $^{1} H +^{1} H$ fusion is the reason that light stars live so long. The slow $^{1} H +^{1} H$ or $p + p$ fusion reaction (see Fig. 2, top left) that triggers the $p p$ chain reactions resembles a sequence of proton capture and helium fusion reactions such as $^{3} He +^{3} He$ , converting the initial hydrogen fuel to $^{4} He$ .

These reactions are among the best studied stellar reaction processes because they are responsible for most of the solar neutrinos [4], which have been successfully observed by underground neutrino detectors such as the Sudbury Neutrino Observatory and Borexino [5,6]. The experimental effort to understand these fusion reactions has centered on underground measurements at the Laboratory for Underground Nuclear Astrophysics (LUNA) facility in the Gran Sasso laboratory in Italy, where critical processes such as the $^{3} He +^{3} He \to 2 p +^{4} He$ [7] and the $^{3} He + α \to γ +^{7} Be$ reaction [8] have been measured to energies within or near the solar Gamow range while complementary studies were performed at above-ground facilities using alternative new techniques [9,10].

In more massive stars ( $M \geq 1.5 M_{sun}$ ), hydrogen burning relies on additional processes—the carbon-nitrogen-oxygen (CNO) cycles—which resemble a sequence of proton capture reactions and $β$ decays on the catalytic carbon, nitrogen, and oxygen isotopes (Fig. 2, top center). This can only take place in second- and later-generation stars, with CNO material being produced by mixed helium and CNO hydrogen burning in first generation stars [11]. Of particular importance is the $^{14} N + p \to γ +^{15} O$ reaction, since it is the slowest reaction in the CNO cycles. The rate of this reaction determines the lifetime of these more massive hydrogen-burning stars—the main sequence stars (Fig. 1). This reaction also determines the flux of the characteristic neutrinos from CNO burning in the solar core, which is presently an issue of great relevance for understanding what fraction of elements in the sun are not hydrogen or helium (i.e., its “metallicity”) [12].

In addition to implications for solar metallicity, the $^{14} N + p \to γ +^{15} O$ reaction is important for tackling larger cosmological questions. The low-energy measurement of reaction has been pursued at the $400$ - $keV$ LUNA II underground accelerator [13–15], and the results have resulted in a substantial reduction of the previously predicted reaction rate at stellar energies, a change that has important consequences for determination of the age of globular clusters and the prediction of the core metallicity of our sun. Globular clusters are very old, gravitationally bound collections of stars that astronomers use to place bounds on the age of the universe. The age of globular clusters is typically determined from the point at which the evolving stars turn off from the main sequence of the distribution of stars in the Hertzsprung-Russell diagram (Fig. 1). For a given age, the lower rate of $^{14} N + p \to γ +^{15} O$ leads to a brighter and bluer turnoff point. For a given turnoff luminosity the revised rate implies a systematically older age for the globular cluster, between 0.7 and 1 billion years [16].

The reduction in this reaction rate will also reduce the flux of solar neutrinos associated with the $β$ decay of the radioactive CNO isotopes $^{13} N$ and $^{15} O$ [12]. This is of particular relevance for the determination of the CNO-dominated core metallicity of our sun, which is presently under debate. The standard solar model predicts the same metallicity for the solar core and the solar photosphere [4]. Helioseismology measurements [17] and spectroscopic analysis of the photosphere abundances [18], however, indicate differences between core and photosphere metallicity. CNO neutrino measurements by SNO-lab [5] and Borexino [6] have been proposed to determine the CNO neutrino flux directly, but ultimately the $^{14} N + p \to γ +^{15} O$ rate is the key for independently extracting the core metallicity from such neutrino flux measurements.

Getting a handle on nucleosynthesis

Stars are the factories in which new chemical elements are formed, and stellar helium burning provides the seed material for a large number of nucleosynthesis processes, which occur during late stellar evolution followed by explosive nucleosynthesis in core collapse supernovae. The energy for these events is generated by the triple $α$ process and the subsequent $^{12} C + α \to γ +^{16} O$ reaction (Fig. 2, right). The triple $α$ process cannot be directly studied and the reaction rate relies on a careful experimental analysis of the various reaction components [19,20]. Most of what we know about the triple $α$ reactions comes from observational evidence from red giant stars, and the associated energy production sets stringent limits to these theoretical predictions [21].

While the triple $α$ process is the main energy source in red giant stars, the subsequent carbon-12 reaction defines the $^{12} C$ , $^{16} O$ abundance distribution for white dwarf stars. White dwarfs are formed as low-mass stars finish burning their helium and begin to contract; their carbon abundance provides the fuel supply for supernova explosions in rapidly accreting white dwarf binaries. For more massive stars, the $^{12} C + α \to γ +^{16} O$ reaction defines the $^{12} C$ , $^{16} O$ seed distribution for the carbon-burning phase. This reaction is therefore of prime importance for late stellar evolution and for the ensuing core collapse supernovae [1].

At low energy, the cross section for this reaction is characterized by a complicated interference pattern between resonant and nonresonant reaction components. Direct studies of the $^{12} C + α \to γ +^{16} O$ reaction [22,23] provide detailed resonance information at higher energies, while indirect measurements of the reaction components through elastic scattering analysis [24] and $β$ -delayed $α$ decay [25] provide complementary data on the strengths of specific reaction components. This is critical information for reducing the uncertainty in the low-energy cross-section extrapolation, which is essential for nailing down the specifics of nucleosynthesis and supernova scenarios.

Heavier elements are also generated by helium burning through the weak slow neutron capture, or “s process,” initiated by the stellar neutron source reaction $^{22} Ne + α \to n +^{25} Mg$ [26]. This neutron source also contributes to s-process nucleosynthesis in hydrogen-helium intershell burning in low-mass asymptotic giant branch (AGB) stars in the Hertzsprung-Russell diagram (Fig. 1) [27]. The reaction is endothermic and therefore extremely sensitive to the temperature. Current estimates suggest that in core helium burning the reaction initiates neutron production only at the final contraction stage of the core of the red giant star [28]. It has been argued that the rate could be substantially enhanced by low-energy resonance contributions [29], yet the experiments have been limited by natural neutron background [30]. The lowest observed resonance at $828 keV$ [30,31] is remarkably strong; no lower energy resonance has been observed yet.

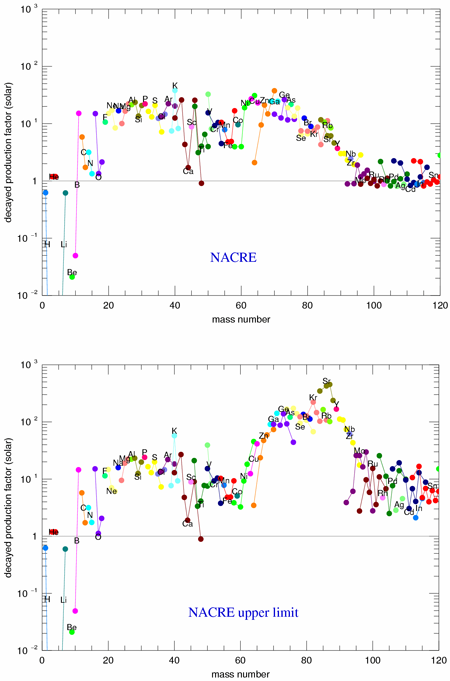
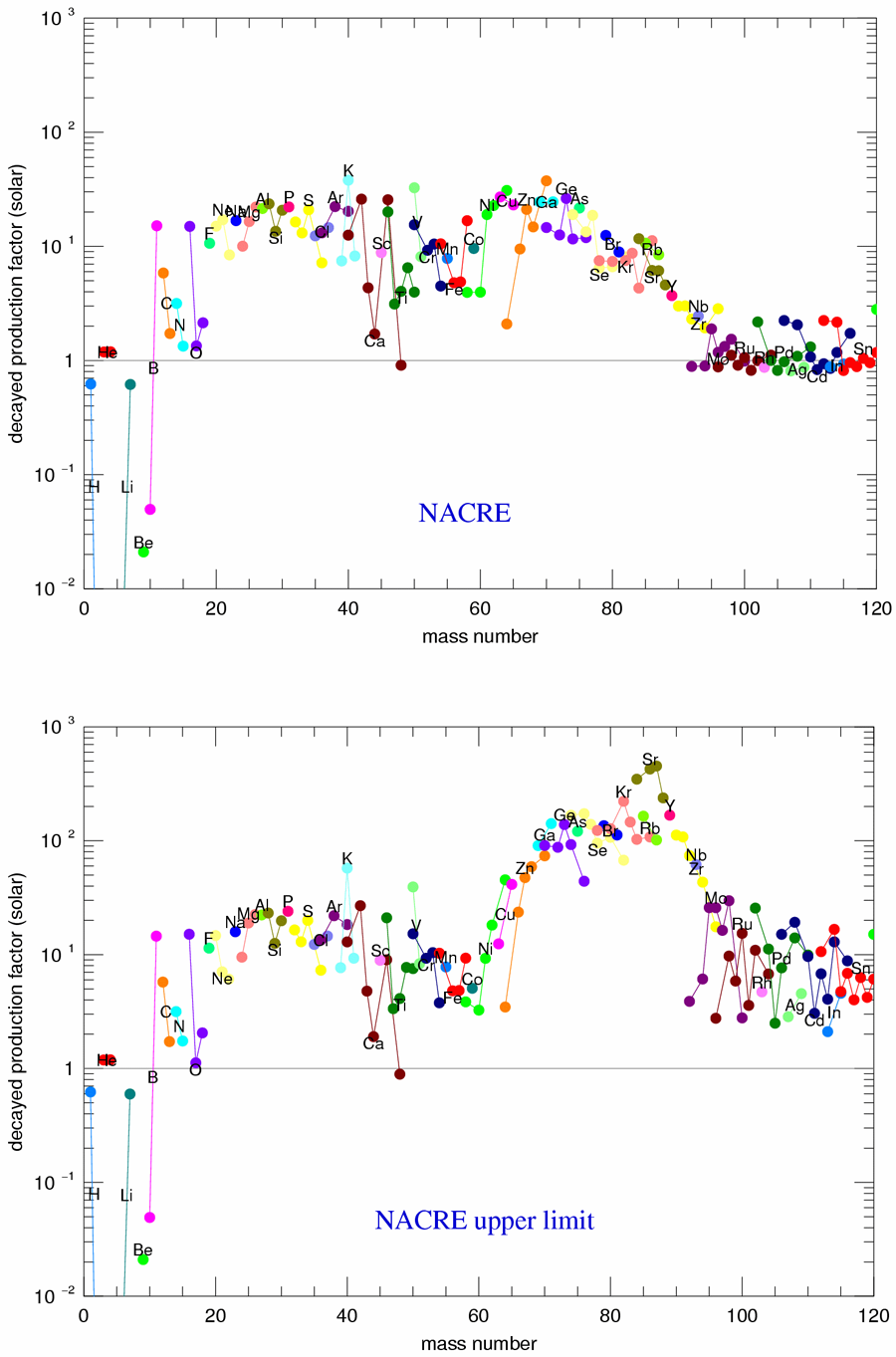
Pinning down isotopic abundances in heavy stars depends on our accurately knowing the $^{22} Ne + α \to n +^{25} Mg$ rate. On the basis of photoexcitation studies [32] a possible state was proposed at $11.154 MeV$ , just above the neutron threshold in $^{26} Mg$ , which could enhance the rate by several orders of magnitude at helium-burning temperatures. This would translate to a substantially higher neutron flux in core helium burning, which causes considerable uncertainty in the s-process abundance predictions for massive stars [33]. Simulations of s-process nucleosynthesis for the lower limit and the upper limit of the presently proposed reaction rate show these huge variations in predicted isotopic abundances (Fig. 4). These uncertainties in s-process abundance predictions have far-reaching consequences. In particular, the nucleosynthesis that occurs in explosive photodisintegration processes (known as p processes) in later supernovae shock fronts [34,35] depends critically on the seed s-process abundances and is therefore directly correlated with the $^{22} Ne + α \to n +^{25} Mg$ reaction rate [36]. A new study of the $^{26} Mg$ photoexcitation reaction with polarized photons at the High Intensity Gamma Source free electron laser facility (HI $γ$ S) at Duke University demonstrated unambiguously that the former spin assignment for the $11.154 MeV$ state was erroneous and that this state cannot be populated by $α$ capture in $^{22} Ne$ nucleus [37].

Further $α$ capture measurements are clearly needed to confirm the results of these indirect studies and to remove all the uncertainties in the complex $^{22} Ne + α$ reaction system. This is one of the main motivations for the installation of a low-energy accelerator at the Deep Underground Science and Engineering Laboratory (DUSEL) at Homestake mine in South Dakota. The reduced cosmic-ray-induced background neutron flux in such a deep underground environment will help to pursue the measurements to a lower energy level than presently accessible.

Carbon fusion and thermonuclear explosions in stars

Our sun’s lifetime and that of other low-mass stars is determined by the $^{1} H + p \to e^{-} + ν +^{2} H$ fusion reaction, while the triple $α$ process ensures the long life of red giant stars like Betelgeuse through stellar helium burning. Following this helium-burning phase, the $^{12} C +^{12} C$ fusion reaction controls the carbon-burning phases in stars during late stellar evolution. But the $^{12} C -^{12} C$ fusion reaction is also highly important because it triggers the ignition of the supernova explosions that occur in accreting white dwarf systems [38]. This reaction is also thought [39] to be responsible for the recently observed superbursts, which are sudden bursts of x-ray activity in accreting neutron star systems that last for much longer time periods than the regular ten second x-ray bursts [40]. However, for the presently accepted reaction rates [28,41,42] the temperatures in the neutron star crust are too low to trigger the ignition of the fusion process at the expected depth in the star [43].

Several decades ago, experimental study of the $^{12} C +^{12} C$ fusion reaction was a major goal [44] (for a summary see Ref. [45]) propelled by the discovery of a pronounced resonance configuration that was interpreted as molecular $^{12} C -^{12} C$ cluster formation [46]. Later measurements [47,48] focused more on the low-energy contributions and confirmed that the lower energy range is characterized by pronounced resonance structures as well. The reaction rate depends sensitively on a reliable extrapolation of the low-energy data to the Gamow range. While the tabulated rate [28] relies on an empirical extrapolation of the data [41], recent attempts use more sophisticated nuclear model techniques [42]. Of particular interest is the suggestion of a “hindrance factor” in the reaction [49]. This would reduce the sub-barrier fusion cross section substantially, which would lead to significant implications for stellar carbon-burning environments [50]. It is clearly of great importance to study the reaction at low energies to provide a more reliable experiment-based reaction rate.

Past experiments were significantly handicapped by natural and beam-induced background problems; over the last decade new experimental techniques have been developed to overcome these difficulties with remarkable success. New results [51] point to the existence of additional low-energy resonances at lower temperatures. Independent of potential hindrance effects, such resonances will dominate the reaction cross section and the stellar fusion rate, as well as the production of protons and $α$ particles for secondary reaction processes in carbon burning. There is speculation about an even lower energy resonance at $1.5 MeV$ [39,52], which could be a pronounced $^{12} C -^{12} C$ cluster state with unprecedented strength [53]. The existence of such resonances will increase the rate by orders of magnitudes with profound consequences for carbon burning since it lowers the ignition temperature substantially. A detailed analysis is needed of the impact of this reduction in ignition conditions within the framework of the various proposed supernovae models [54–56] to evaluate changes in model predictions. In terms of superburst ignition, the reduced ignition temperature would support the suggestion of carbon burning as a trigger for such thermonuclear runaway events in the cold neutron star crust [39].

Studying nuclear reactions underground

Rapid developments in the study of low-energy nuclear reactions should help researchers overcome a number of the challenges that have hampered past work. Theoretical methods have been substantially improved and allow a much more reliable extrapolation of the existing data into the Gamow window of stellar burning. However, theoretical models are often insufficient in describing the complex interaction and interference of the resonant and nonresonant reaction contributions in the Gamow range. There are also possible effects, which occur near the particle threshold, such as contributions from subthreshold resonances or additional nonresonant contributions that have to be taken into account but are only accessible to direct measurement [57].

On the experimental side, new techniques have been developed to push the measurements towards lower energies. The two most remarkable developments are the use of underground accelerator facilities such as LUNA [58] and the utilization of inverse kinematics techniques with large acceptance detectors such as the European Recoil separator for Nuclear Astrophysics (ERNA) at the Ruhr University Bochum [59] and St. George, designed to operate at the University of Notre Dame [60]. Motivated by the success of these facilities, further developments are in preparation, in particular new underground accelerator facilities that will allow researchers to investigate reactions over a wider energy range with a larger portfolio of beams than possible at LUNA. These facilities promise higher energies than are available at LUNA, which is of great relevance for the underground measurements of $α$ capture reactions and stellar neutron sources in helium burning. In particular, it will also improve the chances for pursuing heavy ion fusion reaction studies towards lower energies.

Three major initiatives for the construction of new underground accelerator facilities are now under consideration. A proposal to establish an underground Experimental Low Energy Nuclear Astrophysics (ELENA) accelerator facility at the Boulby salt mine in the UK seeks to take advantage of the reduced level of neutron and natural activity in a salt environment [61]. The disadvantage will be the reduced depth level compared to the Gran Sasso location in Italy. The second is a proposal for the development of a two-accelerator facility DIANA (Dakota Ion Accelerators for Nuclear Astrophysics) at the Deep Underground Science and Engineering Laboratory (DUSEL) at Homestake mine in South Dakota [62]. This would be at a level comparable to Gran Sasso, but with the choice of two accelerators a much broader energy range can be covered, which will also permit the use of heavy ion inverse kinematics techniques (Fig. 5). And third is a proposal being debated to construct an accelerator facility in an abandoned train tunnel in the Pyrenees mountains at Canfranc, Spain [63]. With all of these facilities the nuclear physics community hopes to address the new and critical questions about stellar reaction cross sections and provide the final answer on the nuclear engine of stellar evolution.

References

W. A. Fowler, Rev. Mod. Phys. 56, 149 (1984)
M. La Cognata et al., Phys. Rev. Lett. 101, 152501 (2008)
A. Mukhamedzhanov et al., Phys. Rev. C 78, 015804 (2008)
J. N. Bahcall and M. H. Pinsonneault, Rev. Mod. Phys. 64, 885(1992)
Q. R. Ahmad et al., Phys. Rev. Lett. 87, 071301 (2001)
C. Arpesella et al., Phys. Lett. B 658, 101 (2008)
R. Bonetti et al., Phys. Rev. Lett. 82, 5205 (1999)
H. Costantini et al., Nucl. Phys A814, 144C (2008)
T. A. D. Brown et al., Phys. Rev. C 76, 055801 (2007)
A. Di Leva et al., Phys. Rev. Lett. 102, 232502 (2009)
A. Heger and S. E. Woosley, Astrophys. J. 567, 532 (2002)
W. C. Haxton and A. M. Serenelli, Astrophys. J. 687, 678 (2008)
G. Imbriani et al., Eur. Phys. J. A 25, 455 (2005)
A. Lemut et al., Phys. Lett. B 634, 483 (2006)
R. C. Runkle et al., Phys. Rev. Lett. 94, 082503 (2005)
G. Imbriani et al., Astron. Astrophys. 420, 625 (2004)
S. Basu and H. M. Antia, Phys. Rep. 457, 217 (2008)
M. Asplund et al., Commun. Asteroseismology 147, 76 (2006)
H. O. Fynbo et al., Nature 433, 136 (2005)
K. Ogata et al., arXiv:0905.0007v2 (2009)
A. Dotter and B. Paxton, arXiv:0905.2397v1 (2009)
R. Kunz et al., Phys. Rev. Lett. 86, 3244 (2001)
D. Schürmann et al., Eur. Phys. J. A26, 301 (2005)
P. Tischhauser et al., Phys. Rev. C 79, 055803 (2009)
X. D. Tang et al., Phys. Rev. Lett. 99, 052502 (2007)
M. F. El Eid et al., Astrophys. J. 611, 452, (2004)
M. Busso et al., Ann. Rev. Astron. Astrophys. 37, 239 (1999)
C. Angulo et al., Nucl. Phys. A656, 3 (1999)
F. Käppeler et al., Astrophys. J. 437, 396 (1994)
M. Jaeger et al., Phys. Rev. Lett. 87, 202501 (2001)
P. Koehler, Phys. Rev. C 66, 055805 (2002)
B.L. Berman et al., Phys. Rev. Lett. 23, 386 (1969)
A. Heger et al., New Astr. Rev. 46, 463 (2002)
M. Arnould and S. Goriely, Phys. Rep. 384, 1 (2003)
W. Rapp et al., Astrophys. J. 653, 474 (2006)
V. Costa et al., Astron. Astrophys. 358, L67 (2000)
R. Longland et al. (to be published)
S. E. Woosley et al., Astrophys. J. 607, 921 (2004)
R. L. Cooper et al., arXiv:0903.3994v1 (2009)
J. J. M. in ’t Zand et al., Astron. Astrophys. 411, L487 (2003)
G. Caughlan and W. A. Fowler, At. Data Nucl. Data Tables 40, 283 (1988)
L. R. Gasques et al., Phys. Rev. C 72, 025806 (2005)
A. Cumming et al., Astrophys. J. 646, 429 (2006)
E. Almqvist et al., Phys. Rev. Lett. 4, 515 (1960)
L. Buchmann and C. A. Barnes, Nucl. Phys. A777, 254 (2006)
G. Michaud and E. W. Vogt, Phys. Rev. C 5, 359 (1972)
K. U. Kettner et al., Z. Phys. A 298, 65 (1980)
H. W. Becker et al., Z. Phys. A 303, 305 (1981)
C. L. Jiang et al., Phys. Rev. C 75, 015803 (2007)
L. R. Gasques et al., Phys. Rev. C 76, 035802 (2007)
T. Spillane et al., Phys. Rev. Lett. 98, 122501 (2007)
R. Perez-Torres et al., Phys. Atom. Nucl. 69, 1372 (2006)
http://astronuc.na.infn.it/claus2009/talks.htm.
F. Roepke and W. Hillebrand, Astron. Astrophys. 431, 635 (2005)
F. Roepke et al., Astron. Astrophys. 448, 1 (2006)
T. Plewa et al., Astrophys. J. Lett. 612, L37 (2004)
C. Casella et al., Nucl. Phys. A706, 203 (2002)
D. Bemmerer et al., Eur. Phys. J. A 24, 313 (2005)
D. Rogalla et al., Nucl. Instrum. Methods Phys. Res. Sect. A 513, 573 (2003)
M. Couder et al., Nucl. Instrum. Methods Phys. Res. Sect. A 587, 35 (2008)
http://www.fnuc.es/workshop/Presentaciones/Aliotta.pdf
http://ecrgroup.lbl.gov/DIANA.htm
http://www.fnuc.es/workshop/Presentaciones/Bettini.pdf

About the Author

Michael Wiescher received his Diploma Degree in condensed matter physics at the University of Münster, Germany, in 1974. He received his Ph.D. in nuclear physics at the same university in 1980 with a thesis on stellar hydrogen burning in massive stars. Following post-doctoral research at Ohio State University, the University of Mainz, Germany, and the California Institute of Technology, he joined the faculty of the Physics Department at the University of Notre Dame, in 1986. He holds the Freimann Chair of Physics and serves as the Director of the Nuclear Science Laboratory at Notre Dame and as the Director of the Joint Institute for Nuclear Astrophysics (JINA), an NSF Physics Frontier Center of the University of Notre Dame, Michigan State University, and the University of Chicago. He is also Adjunct Professor at Michigan State University and the University of Surrey, UK. His research interests include the measurement and simulation of nuclear reaction rates and nucleosynthesis processes in stellar evolution and explosion environments. Michael Wiescher is a Fellow of the American Physical Society and the Humboldt Gesellschaft in Germany. In 2003 he was awarded the Bethe Prize of the Divisions of Nuclear Physics and Astrophysics of the American Physical Society. He has given more than 100 invited presentations at national and international conferences and nearly 100 seminars and colloquia, and has published more than 200 refereed articles.