Illuminating molecules from within

Marc J. J. Vrakking

Viewpoint

Illuminating molecules from within

FOM Institute for Atomic and Molecular Physics (AMOLF), Science Park 113, Amsterdam, 1098 XG, The Netherlands

August 31, 2009• Physics 2, 72

Calculations show that with new short pulse x-ray light sources, it should be possible to use photoelectron emission to make movies of changes in molecular structure.

Figure caption — **Figure 1:** (Top) In Young’s double-slit experiment light falls onto two slits and is detected on a screen placed behind the slits. An interference pattern is observed, because one cannot determine whether the light passed through the right or left slit. (Bottom) In the experiment proposed by Hu, Collins, and Schneider, x-ray photons eject the single electron from $H_{2}^{+}$ . The yellow arrow represents the polarization axis of the x-ray beam and the blue arrow represents its propagation direction. The x-ray absorption primarily takes place when the electron is close to one of the two protons, which therefore act as slits. When the angular distribution of the emitted electrons is measured, the internuclear distance between the two protons can be determined.

Much of our knowledge about molecular structure and reactivity is based on interpreting how molecules interact with light. In particular, time-resolved pump-probe studies where a first “pump” laser pulse initiates a dynamical event, and a second “probe” laser pulse interrogates the molecule after it has evolved for some time, provide a very intuitive and insightful view of chemical and biochemical reactivity. In 1999, Ahmed Zewail of Caltech was awarded the Nobel Prize in Chemistry for his groundbreaking role in developing this new field of “femtochemistry.”

In femtochemistry experiments, one usually exploits available knowledge about the way that molecular absorption spectra depend on the instantaneous molecular structure. When the size of a molecule increases, it becomes attractive to rely on diffraction, where structural information is encoded in interference patterns that result from the way that an electron or light wave scatters. In the current issue of Physical Review A, Suxing Hu at the University of Rochester, Lee Collins at Los Alamos National Laboratory, and Barry Schneider at the National Science Foundation, all in the US, describe what such an experiment would reveal in the case of the hydrogen molecular ion $H_{2}^{+}$ , the “fruit fly” of intense field molecular physics research, which consists of two protons and one electron [1].

In their paper the researchers report calculations where the time-dependent Schrödinger equation is solved for the interaction of $H_{2}^{+}$ with an ultrashort x-ray laser pulse. They calculate how the interaction with the laser leads to ejection of the electron, and evaluate its resulting angular and kinetic energy distribution. The structural information that is contained in the angular distributions is twofold. At relatively low photon energies ( $50 eV$ ) the angular distributions contain side lobes, indicating that electrons that acquire their escape energy in the vicinity of one proton can scatter off the other proton before leaving the molecule. Such effects have been observed previously at synchrotrons, e.g., in the photoionization of CO molecules by Landers and co-workers [2].

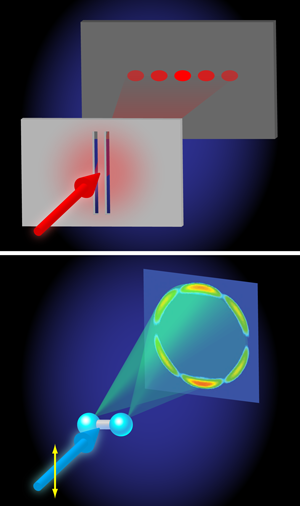
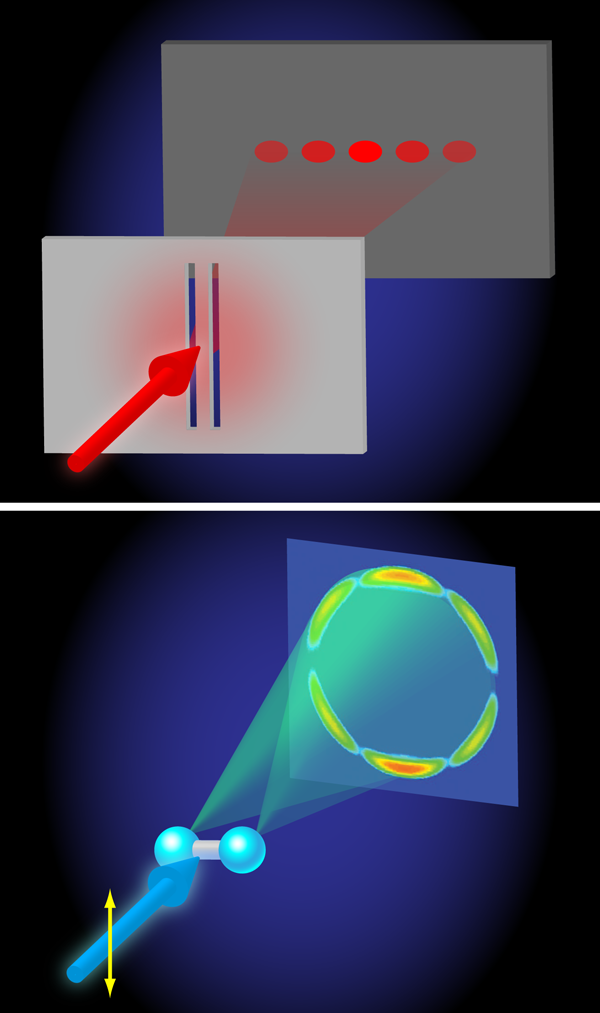
Even more interestingly, at higher photon energies ( $170$ – $650 eV$ ), a beautiful demonstration of the wave nature of quantum mechanics is found. The angular distributions calculated by Hu, Collins, and Schneider reveal an interference between two electron waves that emerge from both protons that is qualitatively very similar to the interference of light waves in the famous double-slit experiment performed by Thomas Young in 1801 (Fig. 1). In Young’s double-slit experiment, light falls on a pair of slits and an interference is detected on a screen placed behind the slits, because it is experimentally impossible to tell through which slit the light moves en route from the light source to the screen. In $H_{2}^{+}$ the two protons act as slits, because the probability for the absorption of x-ray light is highest when the electron is close to one of the two protons. Interference arises because, in the end, it is impossible to tell at which proton the photoabsorption took place. Quantum mechanics then tells us that the wave function amplitudes corresponding to absorption at the left and right proton must be coherently added up, meaning that they will interfere. The interference introduces an oscillation in the angular distribution of the photoelectrons that can be measured, allowing one to determine the separation between the two protons in the $H_{2}^{+}$ ion. In doing so, the wavelength that governs the outcome of the interference experiment is the de Broglie wavelength $λ$ of the emitted photoelectron, which in atomic units is related to its kinetic energy $E_{kin}$ as

$λ = π \sqrt{2 / E_{kin}}$ .

The researchers show that the use of photon/electron kinetic energies $\geq 350 eV$ is sufficient for resolving the internuclear distance of $H_{2}^{+}$ .

Two-center interference in molecular photoionization was already predicted a long time ago by Cohen and Fano [3] and was recently reported in a study on double ionization of $H_{2}$ using synchrotron radiation [4], as well as in a related experiment on photoionization of $N_{2}$ and $CO$ [5]. It is also strongly implicated in experiments where the process of high-harmonic generation (see below) is used to study molecular structure [6]. A particularly interesting study that illustrates how two-source interference can be used to make molecular movies, was performed a few years ago by Sanov and co-workers [7]. In their experiment, $I_{2}^{-}$ negative ions were used, which, in order to start the movie, were excited by a $780$ - $nm$ laser that dissociated the $I_{2}^{-}$ ions into an $I^{-}$ negative ion and a neutral $I$ atom. After a variable time delay, a $390$ - $nm$ photodetachment laser removed the electron from the $I^{-}$ ion. The angular distribution of the electrons was measured and its width was seen to oscillate in time. This oscillation was due to the fact that, as in the previous examples, one cannot distinguish experimentally whether the photodetachment originated from the right or the left iodine atom. Therefore the amplitudes corresponding to these two processes interfered in a constructive or destructive manner, depending on the distance that had accumulated between the two atoms.

In the experiments of Sanov et al., the photodetachment laser produced photoelectrons with a kinetic energy of $0.12 eV (λ_{de Broglie} = 35$ Å). Therefore the interference could only be observed once the molecular dissociation had been completed. However, making use of XUV/x-ray light, the de Broglie wavelength of the ejected electrons can be engineered to be commensurate with the internuclear distances that are encountered in molecules. At that point, it becomes possible to probe molecular rearrangement and dissociation monitoring the two-center interference in time.

In their paper Hu, Collins, and Schneider connect their findings to the recent development of attosecond $(1 as = 10^{- 18} s)$ light sources that operate on the basis of high-harmonic generation [8]. In high-harmonic generation a gaseous atomic or molecular target is exposed to an intense femtosecond laser pulse, and soft x rays are formed by means of a three-step mechanism, where the laser first strips an electron from the atom/molecule, accelerates the electron to a high kinetic energy, and drives it back towards its parent ion, where a recombination can take place that is accompanied by the emission of x rays [9]. While experiments have demonstrated that high-harmonic generation allows the generation of x rays in the $0.5$ – $1 keV$ range [10], it will certainly take some time before attosecond light sources can be focused to the $10^{16}$ – $10^{17} W / {cm}^{2}$ intensities that the researchers talk about in their paper. Rather, the experiments proposed by Hu, Collins, and Schneider seem tailor-made for the Linac Coherent Light Source (LCLS) laser in Stanford, which first achieved lasing on 14 April 2009 [11] and which will begin user operation next month.

LCLS is the world’s first x-ray free electron laser and operates on the basis of the principle of self-amplified spontaneous emission. At the Stanford Linear Accelerator Center electrons are accelerated to $14 GeV$ , before being injected into a series of undulators, where lasing action is achieved. Already during commissioning this spring, LCLS has demonstrated the production of millijoule-level pulses at photon energies that are readily tunable between $0.85$ and $8.5 keV$ , and with a pulse duration that is estimated to be around $75 fs$ . When the number of electrons that are involved in the lasing process is somewhat reduced, the LCLS commissioning team expects that pulses with a duration of only $2 fs$ are formed, i.e., shorter than the time scale for atomic motion in any known chemical process! When focused to a spot of approximately $1 μ m$ diameter, focused intensities on target $\geq 10^{19} W / {cm}^{2}$ should result, significantly exceeding the requirements of the experiments proposed by Hu, Collins, and Schneider. Clearly, the development of LCLS, which in the coming years will be followed by the construction of several similar facilities around the world, represents the starting point of an exciting exploration into new methods that can reveal the nanoscale properties of matter. The experiments proposed by Hu, Collins, and Schneider may soon move from the supercomputer, where they are presently conducted, into the reality of a physics laboratory.

References

S. X. Hu, L. A. Collins, and B. I. Schneider, Phys. Rev. A 80, 023426 (2009)
A. Landers et al., Phys. Rev. Lett. 87, 013002 (2001)
H. D. Cohen and U. Fano, Phys. Rev. 150, 30 (1966)
D. Akoury et al., Science 318, 949 (2007)
B. Zimmermann, Nature Phys. 4, 649 (2008)
T. Kanai, S. Minemoto, and H. Sakai, Nature 435, 470 (2005)
R. Mabbs, K. Pichugin, and A. Sanov, J. Chem. Phys. 123, 054329 (2005)
F. Krausz and M. Ivanov, Rev. Mod. Phys. 81, 163 (2009)
P. B. Corkum, Phys. Rev. Lett. 71, 1994 (1993)
J. Seres et al. Nature 433, 596 (2005)
B. McNeil, Nature Photon. 3, 375 (2009)

About the Author

Marc J. J. Vrakking received his Ph.D. from the University of California, Berkeley, in 1992. After postdoctoral work at the National Research Council in Ottawa, and a KNAW-fellowship position at the Vrije Universiteit Amsterdam, he was a group leader at the FOM Institute for Atomic and Molecular Physics (AMOLF) in Amsterdam from 1997 to 2011. While there, he developed a research program concentrating on the development and application of attosecond laser pulses to study time-resolved electron dynamics and the interaction of atoms and molecules with intense laser fields, as well as the use of free-electron lasers for studying molecular fragmentation processes. In 2010 he was appointed Director at the Max-Born Institute in Berlin, where he now heads a research division devoted to the application of attosecond and high harmonic-based pump-probe spectroscopies to time-resolved studies of atomic, molecular, and cluster dynamics.