Deconstructing the electron

Thierry Giamarchi

Viewpoint

Deconstructing the electron

Thierry Giamarchi

DPMC-MaNEP, University of Geneva, 24, Quai Ernest-Ansermet, CH-1211 Geneva 4, Switzerland

September 21, 2009• Physics 2, 78

An angle-resolved photoemission spectroscopy study of electron transport along quasi-one-dimensional

Mo

-

O

chains of

{Li}_{0.9} {Mo}_{6} O_{17}

reveals puzzling behavior that does not fit within the available one-dimensional theory frameworks and likely points to undiscovered physics.

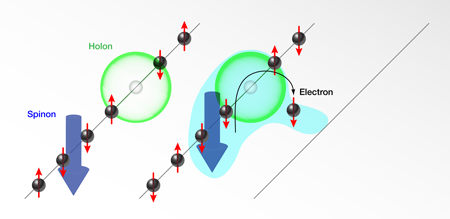
Figure caption — **Figure 1:** In the one-dimensional world, an electron that carries both spin and charge cannot exist as a well-defined particle. It splits into two collective excitations, one carrying spin but not charge (the spinon), the other carrying charge but not spin (the holon). This is one of the basic properties of the Luttinger-liquid theory, the cornerstone for the description of one-dimensional materials. Of course, in a quasi-one-dimensional material where several chains are close to each other, spinons and holons must recombine before a real electron can hop from one chain to the next.

Explaining the behavior of interacting electrons in a solid is one of the long-standing problems in condensed matter. For most systems, the problem has been masterfully addressed by Landau, who showed that even though interactions can be very large, excitations behaving essentially as free fermions still exist in the system. The Landau Fermi-liquid theory allows sweeping the interactions under the rug and saying that the properties of many materials will be very similar to those of free electrons. However, this theory fails spectacularly when an electron gas is confined to one dimension. In that case, a completely new universality class appears, and the Fermi liquid turns into a Luttinger liquid. Single-particle excitations cannot exist, since, as anybody who has queued in a line can readily understand, in one dimension interactions transform any individual motion into a collective one. One-dimensionality has another exotic consequence: excitations can fractionalize. In particular, an externally added electron can split into two collective excitations, one carrying spin but no charge (spinon) and one carrying charge but no spin (holon), see Fig. 1. These strange properties are some of the hallmarks of the Luttinger-liquid theory [1]. They are by now well understood [2] and have been successfully tested in several materials. Now, in a paper published in Physical Review Letters, Feng Wang of the University of Michigan, US, and collaborators from Spain and the US [3] study ${Li}_{0.9} {Mo}_{6} O_{17}$ , a quasi-one-dimensional material nicknamed “purple bronze,” using angle-resolved photoemission spectroscopy (ARPES). They report results that violate the commonly accepted scaling between temperature and frequency imposed by Luttinger-liquid theory in these low-dimensional materials. This challenges our current understanding of these quasi-one-dimensional compounds, and also provides new experimental clues to understand their exciting physics.

Photoemission, as performed by Wang et al., essentially measures the spectral function $A (T, k, ω)$ , which is the probability of observing a single-particle excitation with momentum $k$ and energy $ω$ at temperature $T$ . One can think of a thought experiment consisting of adding a single electron to the system at point $x = 0$ and time $t = 0$ and then measuring the probability of being able to remove it at $(x, t)$ . In a Luttinger liquid, two remarkable properties exist: (a) the single particle correlation function is a power law, decreasing in space and time with an exponent $ν$ dependent on the interactions in the system; (b) as a consequence, the theory is conformally invariant, which means that frequency and temperature play the same scaling role. The implication is that the spectral function, at, e.g., the Fermi momentum, should behave as $A (T, k_{F}, ω$ ) = $T^{η}$ $F (ω / T$ ), where $F$ is some scaling function. Normally, the exponent $η$ should be directly related to the decay of the single particle correlation function $ν$ by the simple scaling law $η$ = $ν - 2$ . However, photoemission performed at different temperatures, as in the work by Wang et al., allows one to independently access $ν$ (from the frequency dependence), and $η$ (from the temperature dependence), and the scaling relation is not obeyed. Indeed, this experiment and previous scanning tunneling microscope (STM) measurements [4] lead to a similar value of $ν \sim$ $1.6$ , implying a negative $η$ instead of the positive value measured.

These findings are surprising, given the generality of the previous argument and the robustness of Luttinger-liquid physics. If the relation between $η$ and $ν$ would hold, the positive value of $η$ would imply a very fast decay of the single-particle correlation function (i.e., a much larger exponent $ν$ ) than anticipated, or indeed directly measured. There could be several ways out of this predicament. The simplest one would be some experimental artifact or surface problem, but that hardly seems compatible with the good quality of the data, the observation of the momentum dependence, the observed scaling, and the agreement between the ARPES and STM measurements. Salvation could come from the theory side: the fact that the material is not a system that can be directly mapped to a single-chain one-dimensional system, but rather to a double-chain one—a ladder system. Those systems are known to develop gaps in their excitation spectrum, in contrast to single-chain ones. Such gaps would be compatible with rapid decay of the single-particle correlations. Of course this would not explain the measured value of $ν$ , or the more severe catch: such gaps should normally be seen in both STM and ARPES, and none have been observed at the relevant energy scales here. Other routes, such as disorder, can be explored but, as of today, the question remains.

Why is it so important to understand this compound since we already have several realizations of Luttinger liquids, and some that work very well? The important point is that purple bronze is in fact a quasi-one-dimensional system (Q1D), made of several one-dimensional chains (or ladders) between which the electrons can, in principle, hop. Depending on the energy at which it is probed, such a Q1D system can follow either the physics of one-dimensional systems with their power-law correlations and deconfined excitations where the electron breaks into spinon and holon, or the more conventional Fermi-liquid physics where single excitations exist and the electron is whole. Quasi-one-dimensional compounds thus normally exhibit a dimensional crossover between one-dimensional and three-dimensional physics when some parameter (say, the temperature) is varied. At large temperatures, the hopping between chains is incoherent and one has one-dimensional physics. At low temperatures, the hopping becomes coherent, leading to three-dimensional physics. How one can reconcile such different physical behaviors, change the nature of the excitations and recombine spinon and holons to bring about the dimensional crossover is a very challenging and important question. One important puzzle is of course whether the low-temperature (“Fermi-liquid”) phase remembers the strong correlations and weird excitations that it experienced in the one-dimensional regime and still retains some exotic properties. One archetypical quasi-one-dimensional system on which such questions have been asked, but are not resolved, is the $(TMTSF)_{2} {ClO}_{4}$ compound, the first organic superconductor [5]. That system has a poorly understood superconducting phase, and by coincidence or not, so does purple bronze. Unfortunately, ARPES is not working very well for $TMTSF$ despite some remarkable studies [6]. The ionic nature of the material probably causes surface problems, which limit the usefulness of such a probe.

In purple bronze, a naive estimate of the crossover temperature, as determined by the interladder hopping energy, would be around room temperature. However, the one-dimensional behavior seems to be observed at much lower temperatures. It is well known that interactions between electrons can lower this temperature, and even potentially drive it to zero [7,2]. Such behavior would be compatible with the rapid decay of the single-particle correlations observed in ARPES: if single-particle correlations decay rapidly it makes it more “difficult” to recombine an electron and jump from one ladder to the next. So all would be well, but of course in that case why is conventional Luttinger-liquid scaling not working for this compound?

Compared to other systems, purple bronze has the advantage of being accessible by a large variety of probes. Wang and collaborators [3] have shown that very detailed ARPES can be performed, giving clear access to the temperature, momentum, and energy of the single-particle excitations. This, combined with the information one can extract from other probes (transport [8], STM, NMR, etc.) should allow this very difficult question of the dimensional crossover, which is relevant for several materials, to be tackled, and perhaps also ultimately give the necessary clues to unravel the mysterious properties of the low-temperature phase in these systems.

References

F. D. M. Haldane, Phys. Rev. Lett. 45, 1358 (1980)
T. Giamarchi, Quantum Physics in One Dimension (Oxford University Press, Oxford, 2004)[Amazon][WorldCat]
F. Wang, J. V. Alvarez, J. W. Allen, S-K. Mo, J. He, R. Jin, D. Mandrus, and H. Höchst, Phys. Rev. Lett. 103, 136401 (2009)
J. Hager, R. Matzdorf, J. He, R. Jin, D. Mandrus, M. A. Cazalilla, and E. W. Plummer, Phys. Rev. Lett. 95, 186402 (2005)
C. Bourbonnais and D. Jerome, in Physics of Organic Superconductors and Conductors, edited by A. G. Lebed (Springer, Heidelberg, 2008), p. 357[Amazon][WorldCat]; T. Giamarchi, ibid., p. 719
M. Grioni, S. Pons, and E. Frantzeskakis, J. Phys. Condens. Matter 21, 023201 (2009)
C. Bourbonnais, F. Creuzet, D. Jérome, K. Bechgaard, and A. Moradpour, J. Phys. Lett. 45, L755 (1984)
X. Xu, A. F. Bangura, J. G. Analytis, J. D. Fletcher, M. M. J. French, N. Shannon, J. He, S. Zhang, D. Mandrus, R. Jin, and N. E. Hussey, Phys. Rev. Lett. 102, 206602 (2009), and references therein

About the Author

Thierry Giamarchi holds a Ph.D. in physics from Paris XI University. A permanent member of France’s CNRS since 1986, he was a postdoc/visiting fellow at Bell Laboratories between 1990 and 1992, and in 2002 he became full professor in the Condensed Matter Department of the University of Geneva. His research focuses on the effects of interactions in low-dimensional quantum systems, such as Tomonaga-Luttinger liquids, and on the effects of disorder in classical and quantum systems. He is a fellow of the American Physical Society and, since 2013, a member of the French Academy of Sciences. In 2010 he was recognized as an Outstanding Referee by the American Physical Society. For more information visit: https://dqmp.unige.ch/giamarchi/thierry-giamarchi/