Shifting entropy elsewhere

Dan  M. Stamper-Kurn

Viewpoint

Shifting entropy elsewhere

Dan M. Stamper-Kurn

Department of Physics, University of California, Berkeley, CA 94720, USA
and Materials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA

September 28, 2009• Physics 2, 80

New methods for lowering the entropy of ultracold gases may allow observation of more subtle quantum materials.

Figure caption — **Figure 1:** Catani *et al.* exchange entropy among quantum gases using element-selective trapping potentials. (a) The schematic diagram shows an admixture of two quantum gases, in which the refrigerator gas (red) and target gas (tan) are held in the same confining potential. Entropy can be transferred from the target gas to the refrigerator gas in two equivalent ways. (b) One approach is to compress the target gas selectively. Catani *et al.* accomplish this using element-specific optical forces, while, in the figure, this is shown schematically by the displacement of an element-specific barrier. (c) A second approach is to expand the refrigerator gas into a larger volume while keeping the volume of the target gas constant, for example, by using an element-specific barrier. While the final temperatures following these two procedures are different, the distribution of entropy between the two gases may be the same. (d) Alternate approaches are being considered where system parameters are tuned spatially so that a quantum gas achieves a gapped phase (shown schematically at left) in one spatial region, and a gapless phase (at right) in a neighboring region into which the entropy will be concentrated. Here, the statistical occupancy of different states is indicated by the size of the shaded circles. Either scheme may allow the preparation of target gases at entropy densities sufficiently low to realize new types of quantum matter.

Ultracold atoms are still too hot. This may seem a ridiculous claim—after all, the low-temperature exploits of the purveyors of quantum gases are notorious. Laser cooling can flash-freeze atoms to temperatures in the micro- and nanokelvin range. In the mid 1990s, researchers followed this with evaporative cooling of atoms out of shallow traps and made the first gaseous Bose-Einstein condensates appear at temperatures of $20 nK$ [1]. With slow and careful cooling by decompression, quantum gases have plummeted to as low as $500 pK$ [2].

So how can such low temperatures still be too high? Let us start with the premise that, over its few-hundred-year-old history, low-temperature physics has sought constantly to discern ever subtler forms of organization in nature. Here, the definition of “subtle” is itself rather subtle, and certainly subjective, but essentially one wants to look beyond obvious forms of order, which arise from stronger and thus more familiar forms of interaction and which are easily described and understood. In a paper in Physical Review Letters, Jacopo Catani and colleagues at the University of Florence and the University of Trento, Italy, now report their exploration of an experimental method for entering a richer realm of quantum ordering [3].

The atomic physics temperature problem is really one of scales, both metaphysical and physical. The troubling metaphysical scale is that of the present scientific ambitions of the cold-atoms community. For many in this community, the cold-atomic materials that have been explored so fruitfully are still too “obvious,” in that mean-field theories with locally defined classical order parameters provide quite suitable descriptions for Bose-Einstein condensates, Cooper-paired Fermi gases, the scalar bosonic Mott insulator state, and so forth. Rather, many want to create forms of matter that are essentially quantum mechanical—the two most-discussed candidates being quantum magnets and analogues of high-temperature superconductors. Such states are marked by strong quantum fluctuations that preclude obvious forms of order and thus allow subtly correlated types of order to arise.

This ultrahigh ambition requires ultralow temperatures because of the physical scales of energy and entropy that are involved. For example, in many proposals for the production of subtle quantum matter, the atoms are assumed to be trapped at roughly a filling factor of unity within a periodic corrugated potential—an optical lattice—established at the intersection of several laser beams. We obtain a natural energy scale $ε_{k}$ as the kinetic energy of an atom with a deBroglie wavelength matching the spacing between lattice sites. With this spacing being on the order of $1 μ m$ and an atomic mass of typically $50 amu$ , we find $ε_{k} \approx k_{B} x 200 nK$ . This temperature scale seems reasonably balmy, but recall that in solid-state systems, with the electron being so much lighter than an atom and the lattice spacing being so much smaller than the wavelength of laser light, the corresponding temperature—related to the electronic Fermi energy—is in the range of $10 000 K$ . Yet the subtle forms of electronic quantum matter probed in today’s laboratories are sought at the kelvin range and below. This discouraging temperature factor of $10^{- 4}$ is partly mitigated in atomic systems by tuning various system parameters. For example, one may seek to generate subtle forms of quantum magnetism, induced by the superexchange spin-spin interaction, in the case where one maximizes interaction energies by resonant interatomic collisions and where the constituent atoms are just barely confined to their lattice sites. Still, temperatures in the sub- (or sub-sub-) nanokelvin range are typically required.

Cold-atoms experimentalists have already glimpsed the subnanokelvin temperature regime. Yet, while the temperature of these ultracoldest gases is suitably low, their entropy remains too high. Indeed, the typical procedure adopted in cold-atom experiments today is to prepare initially bulk quantum gases (bosons, fermions, or admixtures of the two) at the very lowest entropy possible, measured by the ratio $T / T_{Q}$ , where $T_{Q}$ is the quantum degeneracy temperature, and then to ramp up the optical-lattice potentials and/or strong interactions at which the subtle quantum phenomena under study may occur. At best, this ramp-up procedure is isentropic and thus reducing the initial temperature by expanding the gas isentropically is no help. Present lower limits on $T / T_{Q}$ are on the order of $0.05$ , far higher than the $10^{- 4}$ requirement suggested by the analogy to electronic materials.

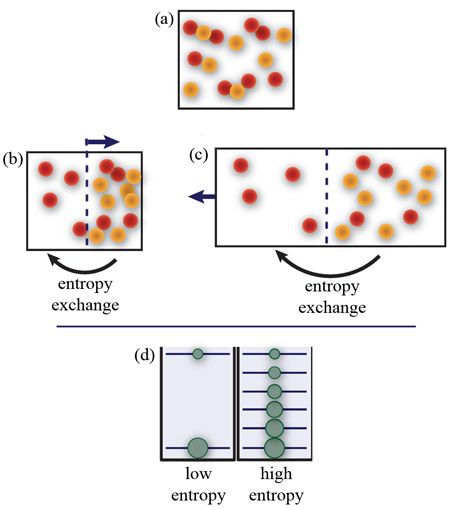
Fortunately, having now identified a barrier to further progress, atomic and condensed-matter physicists are dreaming up many possible solutions. One such solution sees its first implementation in the work by Catani et al. Their strategy mimics that of conventional cryogenics, where studying a new target material does not require inventing a new material-specific direct cooling scheme. Rather, one just places the material within an existing, optimized refrigerator. In their experiment, the Florence-Trento team uses a two-part quantum gas, with one part serving as the refrigerator, and the other as the system targeted for study. Now, expanding just the refrigerator gas so as to lower its temperature makes sense; this colder gas is now able to absorb entropy from the target gas, even if the target gas may be difficult to cool directly due to its being strongly self-interacting or held in a deep optical lattice (see Fig. 1).

To realize this idea, Catani and colleagues produced a quantum-gas admixture of bosonic potassium and rubidium atoms, both held in a common magnetic trap. These different elements have different optical resonances, and thus they experience different optical forces when exposed to the same laser fields. The authors show that the target gas (potassium) is compressed into the focal spot formed by laser light at a particular optical wavelength and polarization, while the refrigerator gas (rubidium) experiences hardly any change. Adiabatically compressing the potassium gas on its own would cause its temperature to rise; however, in the presence of the second gas, this heating is mitigated by the transfer of entropy from the potassium to the rubidium atoms.

There are familiar elements in this work. Sympathetic cooling of one atomic system by another co-trapped atomic species has been demonstrated for both neutral atoms [4] and ions [5], and is now common to many experiments. Element-selective optical trapping was proposed earlier for cooling difficult-to-cool gases [6]. However, the Florence-Trento researchers demonstrate two new elements in their two-element experiment. First, unlike single-shot sympathetic cooling experiments, where the coolant gas lowers the target gas entropy by being irreversibly sacrificed to evaporative cooling, here the authors transfer entropy repeatedly to and fro between the refrigerator and target gases. This is demonstrated by passing the target potassium gas repeatedly across the Bose-Einstein condensation phase transition.

Second, the refrigerator gas serves not only as a reservoir but also as a sensor for the entropy variation of the target gas. If the reservoir gas is a well-understood system—for example, a nearly ideal Bose gas, as in the present work—then measurements of its state variables at two different points in the experiment serve to measure directly both the entropy and temperature changes of the target gas, and thereby to obtain its heat capacity. Variations in the heat capacity can reveal the occurrence of phase transitions in the target gas, even when the nature of those transitions is poorly understood. Recall that our present temperature scale (Kelvin) is defined formally according to properties of an ideal gas thermometer. As such, strapping an ideal gas onto an unknown cold-atomic material seems ideal for calorimetric investigations. In future work, I envision that the refrigerator gas can also serve as a reservoir for magnetization, allowing for the identification of magnetic phase transitions as well.

Other solutions to the quantum-gas entropy problem are also being explored. Several rely on the observation that even in the absence of an additional refrigerator gas, the entropy can be sequestered into specific spatial regions of the target gas, where it may be eliminated by spatially selective culling of the atoms. This spatial entropy redistribution was first demonstrated with a single-component Bose gas in a setup similar to that of Catani et al., and the reversible crossing of the Bose-Einstein condensation transition was similarly achieved [7]. For more strongly correlated atomic systems, the spatial concentration of entropy is aided by varying system parameters (the particle density, for instance) so that regions with gapped excitation spectra abut regions with gapless excitations; at a common temperature, the entropy will be higher in the gapless regions [8,9]. Compared with the scheme offered by Catani et al., this latter approach does not require that an additional refrigerator gas be produced and admixed in a manner that somehow does not vary the behavior of the target system. However, the two-gas scheme is more general, not requiring in-depth knowledge of the target system’s phase diagram.

These days, at any gathering of the cold-atoms community, be it an international topical workshop or an impromptu lab meeting, the challenge of achieving lower entropy quantum gases is sure to come up. One is reminded of the heady days in the development of laser cooling (late 1980s and early 1990s, just before my time) when creative and brash atomic scientists conducted their assorted assaults on the temperature limitations of the day. Their past success gives me confidence that the present barriers will be similarly overcome.

References

M. H. Anderson et al., Science 269, 198 (1995)
A. E. Leanhardt et al., Science 301, 1513 (2003)
J. Catani, G. Barontini, G. Lamporesi, F. Rabatti, G. Thalhammer, F. Minardi, S. Stringari, and M. Inguscio, Phys. Rev. Lett. 103, 140401 (2009)
C. J. Myatt et al., Phys. Rev. Lett. 78, 586 (1997)
D. J. Larson et al., Phys. Rev. Lett. 57, 70 (1986)
R. Onofrio and C. Presilla, Phys. Rev. Lett. 89, 100401 (2002)
D. M. Stamper-Kurn et al., Phys. Rev. Lett. 81, 2194 (1998)
T.-L. Ho and Q. Zhou, Proc. Natl. Acad. Sci. USA 106, 6916 (2009)
J. S. Bernier et al., Phys. Rev. A 79, 061601 (2009)

About the Author

Dan Stamper-Kurn obtained his Ph.D. from MIT for work on Bose-Einstein condensation, and was a Millikan Postdoctoral Fellow, researching quantum optics at Caltech, before joining the Berkeley Physics Department in 2000, where he now holds the Class of 1936 Second Chair in Letters and Sciences and also a joint appointment at the Materials Sciences Division of LBNL. His research utilizes quantum gases to study aspects of condensed-matter physics, quantum optics, quantum atom optics, and quantum and precision measurement. His work is recognized by the 2000 DAMOP Thesis Award of the APS, the Sloan and Packard Fellowships, and the 2003 Presidential Early Career Award for Scientists and Engineers.