Quasiparticles do the twist

Joel E. Moore

Viewpoint

Quasiparticles do the twist

Department of Physics, University of California, Berkeley, CA 94720, USA

October 5, 2009• Physics 2, 82

A theoretical analysis of recent experiments suggests that a key feature of a topological quantum computer—the unusual statistics of quasiparticles in the quantum Hall effect—may finally have been observed.

Figure caption — **Figure 1:** Braiding of quantum Hall quasiparticles. (Left) Adiabatic evolution of a quantum Hall wave function by moving one quasiparticle around another, returning to the original configuration. In fractional quantum Hall states, the result is sensitive to the sense of the “braid” shown (clockwise or anticlockwise). Braids of more than two quasiparticles are mathematically described by a “non-Abelian” group (they need not commute), and in non-Abelian quantum Hall states, the action of braids on the space of wave functions is given by matrices that do not commute. (Right) Sketch of an experimental interferometer with a gate P that effectively moves edge quasiparticles (blue) around bulk quasiparticles (light gray); the total conductance through the point contacts (dark gray) is sensitive to quasiparticle statistics.

One of the most memorable lessons of an undergraduate course in quantum mechanics is that identical particles can have two types of “statistics.” An exchange of two identical bosons leaves the many-particle wave function unchanged, while an exchange of two identical fermions introduces a minus sign. The consequences of this minus sign are profound in all areas of physics. Moreover, it has long been known that two-dimensional systems can have statistics that are neither bosonic nor fermionic. Robert Laughlin’s explanation of the fractional quantum Hall effect introduced quasiparticles with fractional charges such as $e / 3$ . These are thought to possess fractional statistics; if you exchange two identical quasiparticles, the wave function picks up a factor $exp (i ϕ)$ . In more complex quantum Hall states, different quasiparticle exchanges, represented by matrices, do not always commute: the quasiparticles obey non-Abelian statistics.

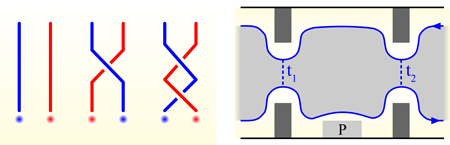
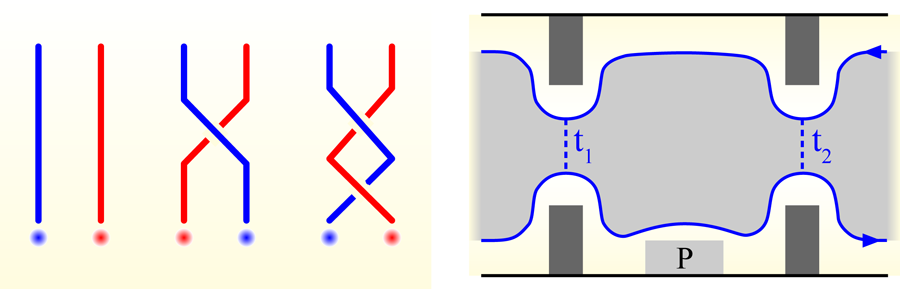
In a theoretical paper in Physical Review B [1], Waheb Bishara and coauthors analyze recent experimental evidence [2] for this remarkable property and discuss how further experiments might probe non-Abelian statistics—an essential ingredient for the “topological quantum computer”—in more detail. Interest in such interferometry experiments has exploded in recent years, driven by the possibility of building a quantum computer that would perform operations by manipulating non-Abelian quasiparticles. The action of a quantum computer can be described by a unitary transformation, and in a topological quantum computer, that unitary transformation is built up of the matrices that describe “braiding” of quasiparticles (Fig. 1, left). These quasiparticle manipulations can be performed while keeping the quasiparticles spatially separated and also maintaining the energy gap between the low-energy states, on which the braiding acts, and others. The resulting advantage over other proposals for quantum computation is that unavoidable small errors in the braiding process, which do not change the topology of the braid, do not degrade the computation.

The existence of fractional statistics is a basic consequence of the “topological order” that defines quantum Hall states in the same way that symmetry breaking defines more conventional states such as superfluids and magnets. Another consequence illustrates better why this type of order is called topological: in many quantum Hall states, the number of degenerate ground states depends on the topology of the system (whether it is a sphere or torus, for example) but not on its geometry. The essence of the quantum Hall effect is that plateaus in the Hall conductance are observed in a two-dimensional (2D) electron gas at certain densities where electrons form a quantum liquid, as first explained by Laughlin [3]. However, the nature of a few quantum Hall plateaus could not be explained by the first generalizations of the Laughlin wave function. The location of a plateau is typically described by the filling factor, which is the density in units of Landau levels (Landau levels are the highly degenerate eigenstates of a single 2D electron in a magnetic field). One unexplained plateau was at filling factor $ν = 5 / 2$ (i.e., two filled Landau levels, plus a half-filled one) where there is no plateau at intermediate temperatures. In high-mobility samples at rather low temperatures, a clear plateau in the Hall conductance does appear at $ν = 5 / 2$ . Gregory Moore and Nicholas Read constructed a remarkable quantum Hall state [4] that Martin Greiter, Xiao-Gang Wen, and Frank Wilczek proposed as an explanation of the plateau at $ν = 5 / 2$ (see Ref. [5]). The Moore-Read state can be viewed as a superconducting state obtained by pair formation from the composite-fermion metal that exists at slightly higher temperatures.

The Moore-Read state was initially appealing on aesthetic grounds and received important numerical support a few years later [6]. Indirect experimental evidence has been accumulating [7], and earlier this year an interferometry experiment by Robert Willett and collaborators observed a remarkable property of the Moore-Read state: its quasiparticles obey statistics that are not just fractional, but non-Abelian. Non-Abelian statistics are possible in a system with degenerate ground states. Moving one quasiparticle around another does not simply multiply the ground state by a phase factor, but acts as a matrix on the whole space of ground states, and the matrices of different quasiparticle “braiding” operations (Fig. 1, left) need not commute. (Here we follow convention in using “ground state” to denote one of the degenerate lowest-energy states with a particular quasiparticle configuration, not the absolute ground state with no quasiparticles.)

The first part of the paper by Bishara et al. critically reviews alternate explanations of the data of this interferometry experiment. All forms of fractional statistics, even the simpler Abelian variety, have been surprisingly difficult to confirm experimentally. While fractional charge can be probed relatively simply, by noise measurements of edge currents [8], for example, a measurement of statistics requires a nonlocal process in which one quasiparticle moves either around another or around a suitable defect. One experiment of this type is a Fabry-Pérot interferometer that coherently combines two paths of a quasiparticle moving along the edge around a bulk region that itself contains quasiparticles (Fig. 1, right).

The actual interferometry experiment is somewhat complicated. As a side gate changes the area of the quantum Hall liquid, one sees oscillations in the total conductance of the two point contacts encircling the liquid. In Abelian quantum Hall states, the oscillations can be understood from the Aharonov-Bohm effect, which now involves the fractional quasiparticle charge, as may have been observed in one of the early quantum Hall interferometry experiments [9]. At $ν = 5 / 2$ , an additional oscillation appears for even values of the number of bulk quasiparticles. This number modifies the point-contact conductance through the braiding effect.

One competing explanation for the observed signal in such an interferometer is the Coulomb blockade effect. When electrons are confined, Coulomb repulsion can give rise to oscillatory features in the tunneling conductance that mimic the Aharonov-Bohm effect [10]. The Coulomb blockade effect would not generally show the same magnetic-field dependence as the Aharonov-Bohm effect, but the field-dependent change in the area of the quantum Hall droplet might cause the effects to appear similar. Bishara et al. consider this and several other scenarios and conclude that current data strongly support the non-Abelian statistics explanation. Future experiments are suggested to distinguish between the Moore-Read state and other proposed states at $ν = 5 / 2$ . In particular, two alternatives that are consistent with the existing experiments are the “anti-Pfaffian” [11] state, which is essentially obtained by “subtracting” the Moore-Read state from filled Landau levels, and the $SU (2)_{2}$ state [12]. Two recent works begin to investigate how interferometry measurements are modified when bulk quasiparticles interact with the edge strongly (i.e., not just through statistics), which may be necessary for a detailed understanding of the experiments [13,14].

Bishara et al. also outline which interferometry experiments would address more complex states than those at $ν = 5 / 2$ . Two families of such states were introduced by Read and Rezayi [15] and by Bonderson and Slingerland [16]. There are at least two motivations for looking at these states. First, observation of the Read-Rezayi candidate state at $ν = 12 / 5$ , for example, would be the first step toward a truly “universal” topological quantum computer. Every operation needed for a quantum computer can be encoded as a braiding of quasiparticles in this state, which is not the case for any of the $ν = 5 / 2$ candidates, nor for the Bonderson-Slingerland candidate at $ν = 12 / 5$ . In the Moore-Read state, for example, the topological braiding operations need to be supplemented by one nontopological operation in order to make a universal computer. Second, observation of the Read-Rezayi state would also be important purely on scientific grounds because its structure is more complex than that of the Moore-Read state. Most of the basic properties of the Moore-Read state appear in any weak-coupling two-dimensional superconductor with “ $p + i p$ ” symmetry of the pair wave function, and the Bogoliubov-de Gennes description of this type of superconductor gives a simple, useful approach, based upon free particles, to the Moore-Read state. The Read-Rezayi state does not seem to have any comparably simple representation.

As these rather complex fractional quantum Hall states are being probed, the topological ideas that came to condensed matter physics via the quantum Hall effect are finding wider application, e.g., in the “topological insulator” materials discovered recently in two [17] and three [18] dimensions. While these discoveries mean that topological phases of electrons can now be studied at room temperature in bulk materials, the most profound examples of how electrons are ordered continue to be found in the physics of the two-dimensional electron gas in a strong magnetic field. The experiments proposed by Bishara and collaborators to separate candidate quantum Hall states at $ν = 5 / 2$ and other fractions will either indicate which existing theory is correct or show that, despite the many aspects of the fractional quantum Hall effect that are understood, there remain mysteries in the statistical interactions of quasiparticles.

References

W. Bishara, P. Bonderson, C. Nayak, K. Shtengel, and J. K. Slingerland, Phys. Rev. B 80, 155303 (2009)
R. L. Willett, L. N. Pfeiffer, and K. W. West, Proc. Natl. Acad. Sci. 106, 8853 (2009)
R. B. Laughlin, Phys. Rev. Lett. 50, 1395 (1983)
G. Moore and N. Read, Nucl. Phys. B 360, 362 (1991)
M. Greiter, X. G. Wen, and F. Wilczek, Nucl. Phys. B 374, 567 (1992)
R. H. Morf, Phys. Rev. Lett. 80, 1505 (1998)
I. Radu, J. Miller, C. Marcus, M. Kastner, L. N. Pfeiffer, and K. West, Science 320, 899 (2008); M. Dolev, M. Heiblum, V. Umansky, A. Stern, and D. Mahalu, Nature 452, 829 (2008)
L. Saminadayar, D. C. Glattli, Y. Jin, and B. Etienne, Phys. Rev. Lett. 79, 2526 (1997); R. de Picciotto et al., Nature 389, 162 (1997)
F. E. Camino, W. Zhou, and V. J. Goldman, Phys. Rev. Lett. 98, 076805 (2007)
Y. Zhang, D. T. McClure, E. M. Levenson-Falk, C. M. Marcus, L. N. Pfeiffer, and K. W. West, Phys. Rev. B 79, 241304 (2009)
S.-S. Lee, S. Ryu, C. Nayak, and M. P. A. Fisher, Phys. Rev. Lett. 99, 236807 (2007); M. Levin, B. I. Halperin, and B. Rosenow, 99, 236806 (2007)
X. G. Wen, Phys. Rev. Lett. 66, 802 (1991); B. Blok and X. G. Wen, Nucl. Phys. B 374, 615 (1992)
B. Rosenow, B. I. Halperin, S. H. Simon, and A. Stern, Phys. Rev. B. 80, 155305 (2009)
W. Bishara and C. Nayak, Phys. Rev. B. 80, 155304 (2009)
N. Read and E. Rezayi, Phys. Rev. B 59, 8084 (1999)
P. Bonderson and J. K. Slingerland, Phys. Rev. B 78, 125323 (2008)
M. König et al., Science 318, 766 (2007)
D. Hsieh et al., Nature 452, 970 (2008)

About the Author

Joel Moore received his A.B. from Princeton and Ph.D. from MIT for theoretical work on the fractional quantum Hall effect. He was a graduate fellow at the Kavli Institute for Theoretical Physics and postdoctoral researcher at Bell Labs before moving to the University of California, Berkeley, and Lawrence Berkeley Laboratory in 2002. His current research interests are in the collective quantum physics of electrons and atoms, including the recently discovered “topological insulators,” and in applications of quantum information concepts to condensed matter physics.