Nearly perfect fluidity

From everyday experience, we have an intuitive feel for how a “good” fluid behaves. A good fluid, such as water, supports complicated flow patterns that decay slowly over time. In contrast, in a “poor” fluid, like honey or tar, we cannot observe waves or eddies, and flow processes decay quickly. Far beyond the realm of the everyday, experiments on ultracold gases and the extremely hot quark-gluon plasma are now allowing us to explore fundamental aspects of fluid mechanics. This article explores how results from studying such seemingly different systems are helping us address the question: Can there be such a thing as a perfect fluid?

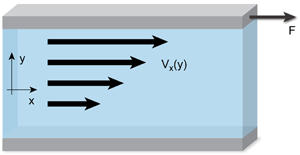
The physical quantity that distinguishes good from poor fluids is the shear viscosity $\eta$ (Fig. 1), which is a measure of the friction force $F$ per unit area $A$ created by a shear flow with transverse flow gradient ${\nabla }_y{v}_x$,

The SI unit for viscosity is a pascal second ( $\text{Pa}\cdot \text{s}$). Given that we define good fluids as having a low shear viscosity, it may be disconcerting to think that the experimental values of $\eta$ for water, liquid helium, cold atomic gases, and hot quark-gluon plasmas—all described as “good” fluids—vary by some 24 orders of magnitude. For example, the shear viscosity of a cold atomic Fermi gas is ∼ $2\times {10}^{-15}\text{Pa}\cdot \text{s}$, while the shear viscosity of the quark-gluon plasma produced recently at the Relativistic Heavy Ion Collider (RHIC)—and dubbed a “perfect fluid”—is $\sim 5\times {10}^{11}\text{Pa}\cdot \text{s}$.

Illustration: Carin Cain

Illustration: Carin Cain

×

Fluid flows are described by a differential equation called the Navier-Stokes equation. The Reynolds number, which is the ratio of inertial to viscous forces in the Navier-Stokes equation, determines the physical behavior of the solutions to this equation. Specifically, the kinds of flows that we associate with good fluidity are characterized by large Reynolds numbers.

The Reynolds number is given by

where $v$ and $L$ are the characteristic velocity and length scale of the flow, respectively, and $mn$ is the fluid’s mass density. We note that the first term, ( $mn/\eta$), is solely a property of the fluid.

Since $mvL$ has units of angular momentum, $\eta /n$ can be measured in units of $\mathrm{ħ}$. The ratio $\eta /(\mathrm{ħ}n)$ is a useful measure of fluidity, but it cannot be directly applied to relativistic fluids for which the particle number is not conserved. Again, we can look to the Reynolds number for guidance. In a relativistic fluid, the Reynolds number is defined in terms of $\eta /s$, where $s$ is the entropy density. Since for many fluids the entropy per particle in units of Boltzmann’s constant $k_B$ is of order one, the ratio $\eta /s$ in units of $\mathrm{ħ}/k_B$ can be used to compare both relativistic and nonrelativistic fluids. Another way to think about the ratio $\eta /s$ is to realize that shear viscosity determines the amount of entropy produced by time-irreversible, dissipative, effects, so this ratio measures the relative change in entropy over a characteristic time $L/v$.

The ratio $\eta /s$ in units of $\mathrm{ħ}/k_B$ for many good fluids is of order one. Water near the triple point reaches $\eta /s\simeq 2$ and measurements in liquid helium give ratios as low as $\eta /s\simeq 0.7$, see Ref. [1] for an overview. This leads us to the question: Can we observe fluids for which $\eta /s$ is arbitrarily small, or is there a fundamental limit to fluidity?

A first hint that a lower limit on viscosity may exist comes from the molecular theory of transport phenomena in dilute gases. This theory goes back to Maxwell, who realized that shear viscosity is related to momentum transport by individual molecules. A simple estimate of the shear viscosity of a dilute gas is

where $n$ is the density, $p$ is the average momentum of the molecules, and $l$ is the mean free path. Since the mean free path varies inversely with the density $n$, the shear viscosity of a dilute gas is, to good approximation, independent of density. The fact that the viscosity of a dilute gas does not depend on its density has some interesting implications. For example, it means that the damping of a pendulum caused by the surrounding air is independent of atmospheric pressure. This counterintuitive result is confirmed by experiment, going back to measurements carried out by Maxwell himself [2].

At fixed density and temperature the shear viscosity is only proportional to the mean free path, which will become shorter as the particles in the fluid start to interact more strongly. We expect, however, that there is a limit to how small $\eta$ can become. Shear viscosity is a measure of the ability of a fluid to transport momentum from one point to another, and quantum mechanics limits the accuracy with which momentum and position can be simultaneously determined. Based on Heisenberg’s uncertainty principle we expect that $pl\gtrsim \mathrm{ħ}$. Using $s\sim k_{B}n$, this relation implies a lower bound of $\eta /s\gtrsim \mathrm{ħ}/k_B$ [3].

There are many possible objections to this simple argument. First of all, kinetic theory is not applicable in the regime $pl\sim \mathrm{ħ}$, because there are no well defined quasiparticles. Also, there are many systems for which the entropy per particle can become much larger than $k_B$. Is it possible to make the lower bound on viscosity more precise?

Perhaps surprisingly, a precise value of the bound on viscosity comes not from transport theory, but from a calculation in string theory. The now famous AdS/CFT (anti-de Sitter/Conformal Field Theory) conjecture says there is a correspondence between certain field theories in four dimensions, and string theory on curved, higher dimensional spaces (see Ref. [4] for a recent pedagogical overview). What is remarkable about the correspondence is that in the limit that the field theory becomes very strongly coupled—meaning the particles of the theory are strongly interacting—the corresponding string theory reduces to classical Einstein gravity. The most studied example of the correspondence is the equivalence between the large $N_c$ limit of a supersymmetric extension of QCD, $\mathcal{N}=4$ superconformal QCD (the CFT of AdS/CFT), and string theory on ${\text{AdS}}_5\times {\text{S}}_5$. Here, $N_c$ is the number of colors in the field theory, ${\text{AdS}}_5$ is five-dimensional anti-de Sitter space—a solution of the Einstein equations with a negative cosmological constant—and ${\text{S}}_5$ is a 5 sphere. The boundary of ${\text{AdS}}_5\times {\text{S}}_5$ is four-dimensional Minkowski space. In order to study the boundary theory at finite temperature one has to consider solutions of Einstein’s equations that contain a black hole in the ${\text{AdS}}_5$ space. The temperature of the field theory is equal to the Hawking temperature of the back hole.

The shear viscosity of a plasma that sits on the boundary of this space is determined by the absorptive part of the stress tensor correlation function. The stress tensor is the source of a gravitational field in the five-dimensional geometry, and the shear viscosity of the plasma can be related to the absorption of gravitational waves by the black hole. Policastro et al. computed $\eta /s$ in the strong coupling limit of superconformal QCD and found [5] that it was equal to

This result is universal—it applies to all theories that have a classical gravitational dual—and any corrections to account for the fact that the coupling in the CFT is not infinite will only increase the ratio $\eta /s$. Kovtun, Son, and Starinets (KSS) conjectured that $\eta /s\ge \mathrm{ħ}/(4\pi k_B)$ is a universal lower bound, valid for all fluids [6]. We now know that this conjecture is not strictly true—there are theories in which corrections lower the ratio $\eta /s$—but these violations are themselves bounded [7]. However, the precise value of the universal lower bound is not known at present.

The shear viscosity to entropy density ratio of helium exceeds the KSS bound $\mathrm{ħ}/(4\pi k_B)$ by almost an order of magnitude. But are there fluids in nature that approach this lower bound? Remarkably, the two best candidates are the coldest and hottest fluids that can be produced in the laboratory.

The coldest fluid is made from optically trapped ${}^6\text{Li}$ atoms. ${}^6\text{Li}$ is a fermion, and it can be trapped in two different hyperfine states. We can view these states as the “up” and “down” states of a nonrelativistic spin $1/2$ particle. The interaction between spin-up and spin-down particles can be tuned via a Feshbach resonance, where the two particles form a bound state with zero binding energy. On resonance the two-body scattering length diverges and at this so-called “unitarity limit” the only dimensionful quantity describing the atomic gas is the particle density. As a consequence, the viscosity in units of $\mathrm{ħ}$ must be a multiple of the density $n$.

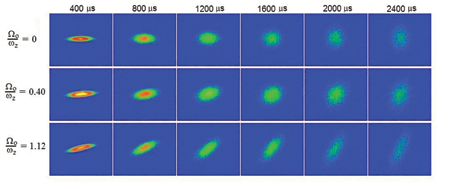
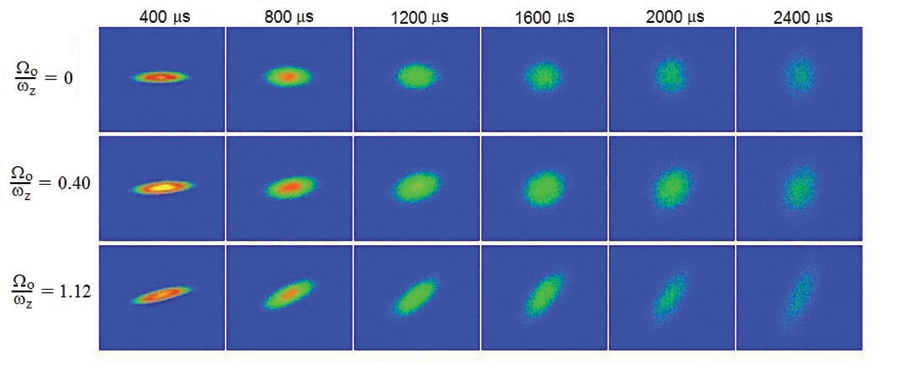
Nearly perfect fluidity is observed in experiments on cold atom gases like the one shown in Fig. 2 (from Ref. [8]). The top row shows the expansion of a Fermi gas out of a deformed trap after the trapping potential is removed. In hydrostatic equilibrium the pressure gradient in the short (transverse) direction is larger than the one in the long (axial) direction. After the potential is removed this pressure gradient accelerates the cloud in the transverse direction, and the cloud eventually elongates in the short direction. Shear viscosity tends to counteract this expansion and at unitarity, the expansion is consistent with almost ideal hydrodynamics.

×

Additional information is obtained if the gas is released from a slowly rotating trap, as in the second and third row of Fig. 2. As the cloud becomes spherical, the rotational motion speeds up, which implies that the moment of inertia is suppressed. This is the hallmark of irrotational flow, which is usually observed in superfluids, but at unitarity the moment of inertia is also suppressed in the normal phase of a fluid. A quantitative analysis of the data shown in Fig. 2 was reported by John Thomas from Duke University in Ref. [9]. He finds $\eta /s\simeq (0.1-0.5)$ in units of $\mathrm{ħ}/k_B$. This value is even smaller than an earlier estimate, $\eta /s\lesssim 0.5$, based on an analysis of the damping of collective oscillations [10].

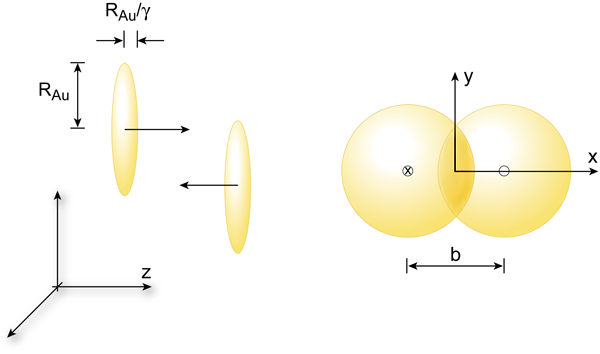
Almost ideal hydrodynamic flow was also observed in a completely different physical system, the quark-gluon plasma created in heavy-ion collisions at RHIC at Brookhaven National Laboratory [11–13]. The conditions for creating the quark gluon plasma could not be more different from the optically trapped cold ions: The energy in gold-gold collisions at RHIC is $100\text{GeV}$ per nucleon, and the nuclei are Lorentz contracted by a factor of $\gamma \simeq 100$. The transverse radius of a gold nucleus is approximately $6\text{fm}$, and on the order of $7000$ particles are produced overall. The motion of the particles is relativistic, and the duration of a heavy-ion event is $\sim 6\text{fm}/\text{c}$—about ${10}^{-23}\text{s}$. In order for hydrodynamic theory to apply to the quark-gluon plasma, this time has to be large compared to the time it takes for the plasma to equilibrate.

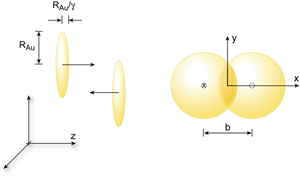
The most dramatic evidence for hydrodynamic behavior in the quark-gluon plasma is the observation of elliptic flow in noncentral heavy-ion collisions (see Fig. 3 for a schematic illustration of the geometry). Elliptic flow occurs when the plasma collectively responds to pressure gradients in the initial state, just as in the case of cold atomic gases. Hydrodynamic evolution converts the initial pressure gradients to velocity gradients in the final state.

Illustration: Carin Cain

Illustration: Carin Cain

×

In a heavy-ion collision we cannot control the deformation of the initial state, as we can by using specially designed traps for cold atom gases. Instead, the deformation of the plasma is determined by the shape of the overlapping region of the colliding nuclei. This shape is governed by the impact parameter $b$, the transverse separation of the two nuclei (Fig. 3). The impact parameter can be measured on an event-by-event basis using the azimuthal dependence of the spectra of produced particles. Once the impact parameter direction is known, the particle distribution can be expanded in Fourier components of the azimuthal angle $\varphi$:

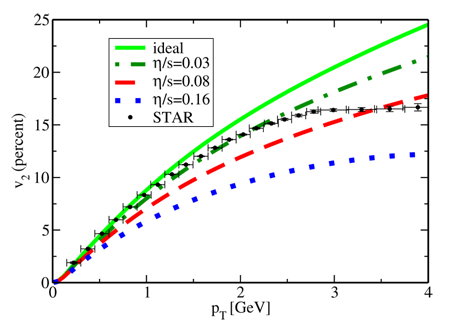
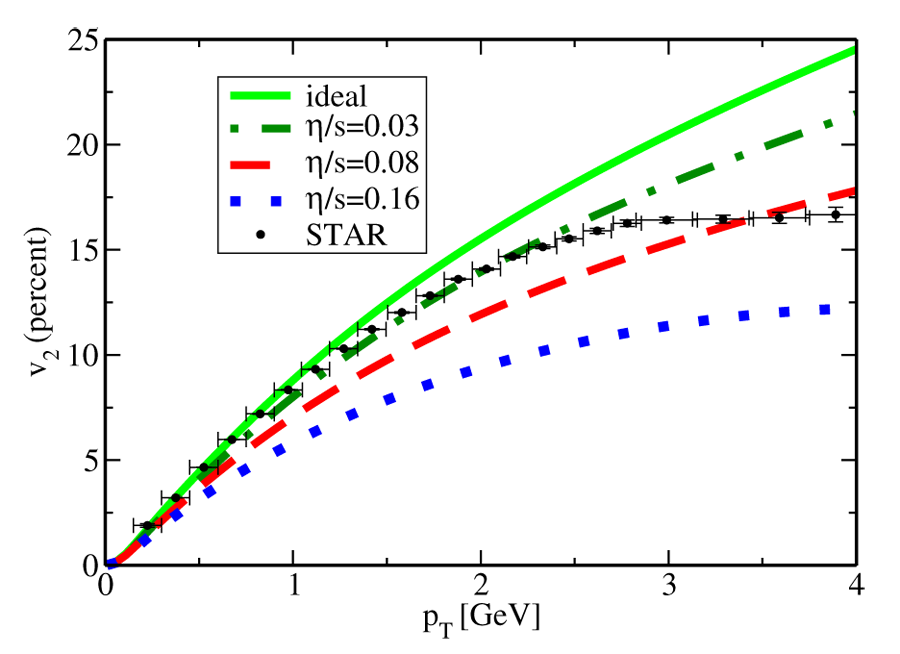
where $N$ is the number of particles, $p_0$ is the energy, and $p_T=(p_x^2+p_y^2{)}^{1/2}$ is the transverse momentum. The Fourier coefficients $v_2,v_4,$ carry information about the deformation of the final state and, in particular, a positive $v_2$ harmonic implies that particles are preferentially emitted in the short direction, i.e., elliptic flow, just as in the cold atomic gases. Figure 4 shows that the experimentally measured elliptic flow coefficient can become as large as $15\%$, which corresponds to a significant deformation in the anisotropy of the particle distribution $(1+2v_2)/(1-2v_2)\simeq 1.85$.

×

Shear viscosity slows down the transverse expansion of the system and reduces $v_2$. A quantitative analysis of the RHIC data, taken from the work of Paul Romatschke and Ulrike Romatschke, is shown in Fig. 4 [14]. Similar analyses can be found in [15,16]. We observe that the best fit to the data is obtained for $\eta /s\simeq 0.03\mathrm{ħ}/k_B$. (Note that the hydrodynamic fit is not expected to describe the spectra for $p_T>2\text{GeV}$, because particles in this range of momenta are rare and have large mean free paths and therefore don’t reach equilibrium on such short time scales.) The best fit value of $\eta /s$ is smaller than $\mathrm{ħ}/(4\pi k_B)$, but there are significant uncertainties associated with the anisotropy of the initial state, which cannot be directly measured, and hydrodynamics breaks down in the late stages of the evolution when quarks and gluons hadronize into the observed particles, such as pions, kaons, and nucleons. A conservative bound from the RHIC experiments is $\eta /s\lesssim 0.4\mathrm{ħ}/k_B$. Current work on both the cold atomic gases and the quark gluon plasma is devoted to sharpening these numerical estimates, and to correlate the shear viscosity with other transport properties, like the energy loss of energetic probes.

Ultimately, we would like to understand what nearly perfect fluids are like: Is momentum transport governed by quasiparticles, or are there no quasiparticles at all, as suggested by the AdS/CFT correspondence? There are several ways to address this question. One approach is to use quantum Monte Carlo calculations to compute the spectral function of the energy-momentum tensor. Kinetic theory predicts that the spectral function contains a peak associated with the contribution of quasiparticles, whereas the AdS/CFT correspondence leads to a completely smooth spectral function.

Experimentally, we can study the way hydrodynamics break down as one goes to smaller or even more deformed systems, and how shear viscosity is correlated with other transport properties like the diffusion constant. In heavy-ion collisions, diffusion can be studied by measuring the extent to which heavy charm and bottom quarks follow the flow of light quarks. Heavy quarks are rare, and in the experiment their trajectories have to be reconstructed from their decay products. As a consequence, flow data for heavy quarks has not yet reached the accuracy that has been achieved for light quarks.

Finally, both theorists and experimentalists are eagerly awaiting data from the Large Hadron Collider (LHC) at CERN. The LHC will be able to produce a higher temperature quark-gluon plasma than that RHIC can currently reach. Data on elliptic flow will tell us whether hydrodynamics continues to be applicable under these conditions, and how the “perfection” of the hot plasma at the LHC compares to what was seen at RHIC.