Slipping through blood flow

Howard A. Stone; Alison M. Forsyth; Jiandi  Wan

Viewpoint

Slipping through blood flow

Howard A. Stone, Alison M. Forsyth, and Jiandi Wan

Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA

October 26, 2009• Physics 2, 89

Simulations provide insight into how viscous flow transforms the shapes of red blood cells, which may influence their physiological properties.

Figure caption — **Figure 1:** The motion and shape of red blood cells depends on the flow environment. (Top) The shape of a red blood cell at rest is symmetric, with both sides of the membrane concave. (Bottom left) The velocity profile of the fluid that carries the cells through a blood vessel is assumed to have a symmetric parabolic shape. (Bottom right) The simulated shapes of the cells as a function of the surrounding flow velocity and their reduced area $ν$ , which is the ratio of their area to the area of a circle with a circumference equal to the perimeter of the cell. Below a certain value of $ν$ , the cells are unstable to forming an asymmetric shape (from Ref. [1]).

Coronary artery disease—the leading cause of death in the United States—results from the formation of plaque in our arteries, which blocks the transport of blood. The movement and deformation of red blood cells can also affect the flow of blood, and vice versa, but the mechanics of this relationship is still being explored. Writing in Physical Review Letters, Badr Kaoui and Chaouqi Misbah at Université Joseph Fourier in Grenoble, France, and George Biros at the Georgia Institute of Technology in the US explore, with simulations, how flow deforms red blood cells [1]. Their numerical simulations show that an experimentally observed transition in the shape of red blood cells, from symmetric to asymmetric, occurs even when the cells (which the authors model as vesicles) move in a fluid with a symmetric flow velocity distribution. They suggest that this shape transition, which arises because the symmetric shape is unstable, may be able to influence the flow efficiency for red blood cells. As recent research links the chemical responses of red blood cells to their mechanics, such models of individual shape transitions of cells could offer further understanding of physiological flows.

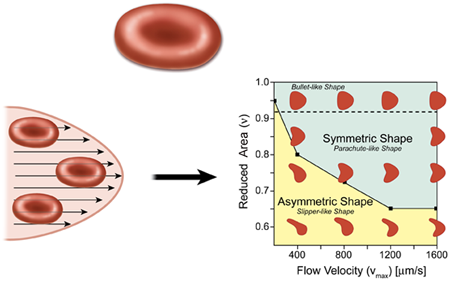
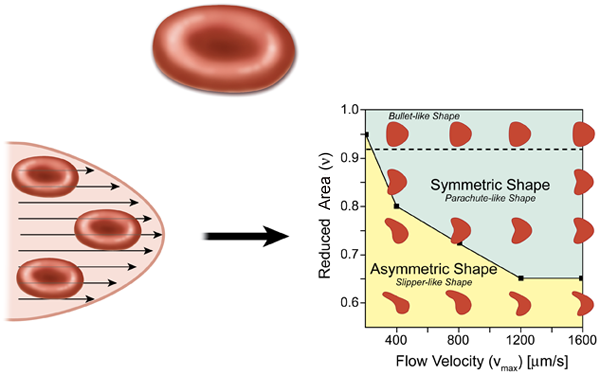
In the most elementary model for flow in the circulatory system, the heart acts as a pump, which drives the fluid containing red blood cells (blood) through circular tubes. In this case we expect the profile of the velocity to have a parabolic shape (Hagen-Poiseuille flow), as in the lower left part of Fig. 1. For a constant pressure drop, the volumetric flow rate of the fluid is proportional to the radius of the tube to the fourth power, which suggests that the diameter of blood vessels will play an important role in controlling blood flow. The natural expectation for a single red blood cell in a microvessel flow, which is assumed to have a parabolic velocity profile, is that it will be confined and should form a symmetrical shape in the center of the symmetrical flow. This result, however, is not necessarily the case, as pointed out by Kaoui et al.

A common model for red blood cells is a vesicle, which is a drop of liquid that is completely enclosed by a bilayer made from the same kind of phospholipid molecules found in cell membranes. Red blood cells are different from vesicles in that they have a cytoskeleton protein network underneath the lipid bilayer membrane, which gives the system a shear elasticity and supports a biconcave shape (about $8 μ m$ in diameter) under static conditions (top of Fig. 1). Under flow conditions, however, the fact that the cell can deform contributes to the viscous energy dissipation of the flow. For example, a red blood cell can tumble, as a rigid body, and tank-tread, where the cell maintains a constant orientation in a flow while the membrane rotates around the cell’s cytoplasm. There is also a symmetric “parachute” cell morphology where the cell deforms as a result of viscous forces, but keeps a symmetric shape and therefore cannot tank-tread.

In vivo studies have already demonstrated that red blood cells do in fact form asymmetric shapes in vessels that are less than $20 μ m$ , which is only a little larger than the cell itself [2]. In the presence of large viscous forces, the cell deforms asymmetrically into a “slipper” shape [3]. These asymmetric cells tank-tread because asymmetric viscous forces—produced by the cell’s asymmetric shape or the nonsymmetric position of the cell relative to the long axis of the vessel—act on the membrane. This “slipper” shape, which is a consequence of the confinement of the cell in a close-fitting channel, is believed to substantially reduce viscous dissipation [4].

With their simulations, Kaoui et al. have tried to address the question of how the cell shape changes as a consequence of the detailed flow structure, largely in the absence of direct interactions with a wall. For simplicity, they model the red blood cells as vesicles and assume they move in a plane in a symmetric parabolic flow. They find that the shape transition results from a loss in stability of the shape, which occurs when a dimensionless vesicle deflation number $v$ , defined as the ratio of the actual area to the area of a circle with a circumference equal to the perimeter of the cell, is below a certain value. ( $v$ is always less than $1$ , unless the cell is a circle.) Below the critical value of $0.7$ , the symmetric parachutelike shape develops an instability and the cell transforms into an asymmetric slipperlike shape (Fig. 1, right). Most importantly, this transition is not dependent on either the confinement of the surrounding blood vessel walls or membrane shear elasticity, which provides a new perspective for understanding the dynamics of red blood cells under flow conditions. Kaoui et al. also point out that this shape transition causes a decrease in the velocity difference between the cell and the flow, which could potentially enhance the efficiency of blood flow.

Kaoui et al.’s model is limited to two-dimensional vesicles and it is unclear if their results translate to more realistic three-dimensional models of red blood cells. Moreover, confinement and shear elasticity were shown to be unnecessary in this particular case, e.g., there was no direct wall effect, but such confinement influences may still play roles in shape transitions under different circumstances. Nevertheless, experiments on red blood cells have shown that viscous shear stresses in the flow control the transition from a symmetric parachutelike shape to an asymmetric slipper shape and that confinement is not necessary for the slipper shape [5], both conclusions that are consistent with the results of Kaoui et al.

The study of Kaoui et al. is an important contribution to the field of cell dynamics, but the role this shape transition plays in other physiological factors has yet to be examined theoretically or experimentally. For example, the effect of the density of red blood cells on this shape transition has not been explored and could result in cell clustering [6]. Adenosine triphosphate (ATP), which is released by red blood cells and can cause blood vessel dilation in vivo, has been correlated with cell deformation [7,8]. The role that the shape transitions discussed above play in the release of ATP or other chemicals thus will have interesting ramifications for both circulatory physiology and pathophysiology. In addition, as suggested by Kaoui et al., it has not been elucidated what role tank-treading or the lack thereof, plays in oxygen transport, which is the main function of red blood cells.

References

B. Kaoui, G. Biros, and C. Misbah, Phys. Rev. Lett. 103, 188101 (2009)
R. Skalak and P. I. Branemark, Science 164, 717 (1969)
P. Gaehtgens, C. Dührssen, and K. H. Albrecht, Blood Cells 6, 799 (1980)
P. Gaehtgens and H. Schmid-Schönbein, Naturwissenschaften 69, 294 (1982)
M. Abkarian, M. Faivre, R. Horton, K. Smistrup, C. A. Best-Popescu, and H. A. Stone, Biomedical Materials 3, 13 (2008)
J. L. McWhirtera, H. Noguchi, and G. Gompper Proc. Natl. Acad. Sci. U.S.A. 106, 6039 (2009)
A. K. Price, D. J. Fischer, R. S. Martin, and D. M. Spence, Anal. Chem. 76, 4849 (2004)
J. Wan, W. D. Ristenpart, and H. A. Stone, Proc. Natl. Acad. Sci. U.S.A. 105, 16432 (2008)

About the Authors

Howard A. Stone is the Donald R. Dixon ’69 and Elizabeth W. Dixon Professor in Mechanical and Aerospace Engineering at Princeton University. He received his S.B. degree in chemical engineering from the University of California, Davis, and a Ph.D. in chemical engineering from Caltech. From 1989 to 2009 he was on the faculty in the School of Engineering and Applied Sciences at Harvard University. His research interests are in fluid dynamics, especially as they arise in research and applications at the interface of engineering, chemistry, and physics. He was the first recipient of the G. K. Batchelor Prize in Fluid Dynamics, which was awarded in August 2008. In 2009 he was elected to the National Academy of Engineering. In 2008 he was recognized as an Outstanding Referee by the American Physical Society.

Alison M. Forsyth is a Ph.D. candidate at Harvard University in the School of Engineering and Applied Sciences and is currently a visiting scholar at Princeton University in the Department of Mechanical and Aerospace Engineering. She completed her B.S. in bioengineering at Syracuse University in 2006. Her research involves red blood cell deformation and dynamics with implications for physiological responses in the cardiovascular system.

Jiandi Wan is currently a Research Associate in the Department of Mechanical and Aerospace Engineering at Princeton University. His degrees are in chemistry from Wuhan University (B.S., 1998, M.S., 2001) and Boston University (Ph.D., 2006). Dr. Wan worked as a postdoctoral researcher in the School of Engineering and Applied Sciences at Harvard University from 2006 to 2009 and moved to Princeton University in 2009. Dr. Wan’s research includes microfluidic approaches for studying red blood cell dynamics and multiphase emulsions, photoinduced electron transfer dynamics, and surface chemistry. His recent work focuses on the material and biophysical applications of microfluidics.