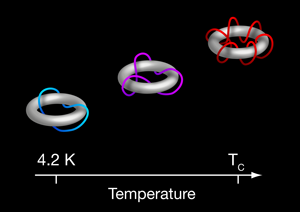
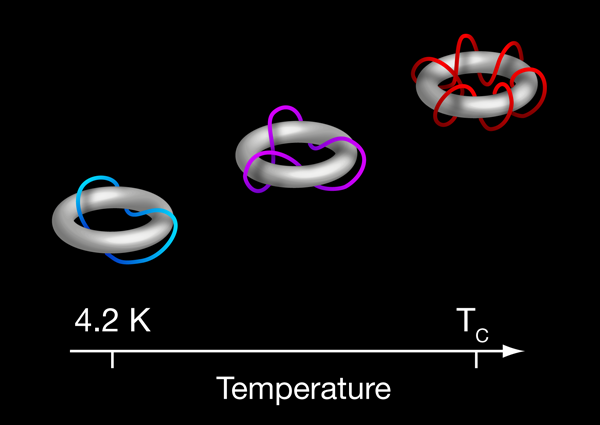
Can superconducting rings provide clues to the early development of the universe?

John R. Kirtley; Francesco Tafuri

Viewpoint

Can superconducting rings provide clues to the early development of the universe?

John R. Kirtley

Center for Probing the Nanoscale,Stanford University, McCullough Building, 476 Lomita Mall, Stanford, CA 94305-4045, USA

Francesco Tafuri

Dipartimento di Ingegneria dell’Informazione, Seconda Università di Napoli, and CNR-INFM Coherentia/NEST, Via Roma 29, 81031 Aversa (CE), Italy

November 2, 2009• Physics 2, 92

Defects—in the form of vortices in superconductors or “strings” in the fabric of the universe—can reveal the state of a system at the time it was cooled.

Figure caption — **Figure 1:** As a metal ring is cooled below its superconducting transition temperature $T_{c}$ , the phase of different regions of the ring will be out of sync. The winding lines indicate the rotation in the phase of the superconducting wave function around the ring.

Watching a metal transform into a superconductor, it may not be obvious that this transition provides access to some of the same physics that governed the cooling of the universe following the Big Bang. Yet at the root of both of these phenomena—albeit at astronomically different energy scales—is the question of how defects form in a continuous phase transition. In a paper appearing in Physical Review B [1], Roberto Monaco at the Università di Salerno in Italy, Jesper Mygind at the Technical University of Denmark, Ray Rivers at Imperial College London, UK, and Valery Koshelets at the Russian Academy of Science in Moscow have taken ideas about the early development of the universe and applied them to the dynamics of the superconducting phase transition in metal rings. In doing so, they introduce an elegant way to measure the tiny flux quanta that are trapped at the centers of these rings, and develop a new understanding of how the cooling process works in mesoscopic systems.

Symmetry principles and how they are broken are fundamental concepts in physics, including our picture of what happened after the Big Bang. The unification of the electromagnetic, weak, and strong forces came from realizing that at high energies, a fundamental symmetry relates the particles that mediate these interactions. However, over time as the universe cooled to our “low-energy” world, this symmetry was broken, which is why the $W$ and $Z$ bosons, which mediate the weak interaction, have mass, while the photon, which mediates the electromagnetic force, does not.

Just as there is a lattice mismatch between regions of a liquid that crystallize with different orientations, defects formed as a result of the universe going through a symmetry breaking phase transition. Theorists postulated that the defects associated with the rapid cooling of the universe—imagined as strings, monopoles, and domain walls—could serve as imprints of the universe at the point at which they were formed. Within this context, Tom Kibble proposed an intuitive picture of the “freezing out” of the early universe and the typical length scale between defects [2,3]. Underlying his picture was the idea that causality—that a finite time delay is needed for information to be transferred between different regions of a system—governed the number of defects.

Wojciech Zurek [4] noted that although Kibble’s ideas involved processes with energies far too high to be accessible in the laboratory, they could be tested in the realm of condensed matter by studying the defects, called vortices, that form in superfluids and superconductors. Figure 1 provides a helpful visualization of Kibble and Zurek’s basic idea for a superconductor. The transition from the normal (metallic) to the superconducting state is a symmetry breaking transition and the order parameter that describes the onset of the superconducting phase has an amplitude $ψ$ and a phase $φ$ . Assume for simplicity that in the rings in Fig. 1, $ψ$ is spatially independent and the ring is sufficiently narrow that $φ$ depends only on the azimuthal angle $θ$ . As the ring cools through the superconducting transition temperature $T_{c}$ , $ψ$ will become larger, but different sections of the ring will randomly assume different values of $φ$ . This happens because locally, the superconducting phase is forming faster than it can communicate with other regions in the ring. This will produce “kinks” or “defects,” regions where $φ$ would eventually (at low temperature) change by a factor of $2 π$ . These kinks can be removed by annihilation with anti-kinks if the coherence length $ξ$ —the region over which the Cooper pairs in the superconductor share the same phase—is long enough and if the cooling rate is sufficiently slow. However, as the system cools this annihilation process proceeds less and less rapidly, until at some point the kinks “freeze in” because parts of the system cannot communicate with other parts quickly enough.

In the case of a superconducting ring, the net change in phase around the ring is limited to $2 π$ $n$ , where $n$ is an integer. Associated with this quantized phase are quantized values of supercurrents circulating around the ring and magnetic flux threading through it. For this reason, this process of forming defects is also called spontaneous fluxoid generation.

Kibble and Zurek showed that causality governs the final probability of finding a spontaneous fluxoid in the ring after it is cooled. Specifically, causality implies that the probability of finding a single fluxoid in the ring (when cooled in zero external field) depends on the cooling (quench) rate $τ_{Q}^{- 1}$ as $\propto (τ_{Q} / τ_{0})^{- σ}$ , where $τ_{0}$ is a characteristic time and the exponent $σ$ depends on the details of how the correlation length $ξ$ and the relaxation time $τ$ vary with temperature close to the transition. For a superconducting ring and assuming a mean-field approximation, $σ = 1 / 4$ .

Kibble and Zurek’s prediction has been tested in a number of experimental systems by looking for vortices in superfluid $^{4} He$ (see Refs. [5,6]) and $^{3} He$ (see Refs. [7,8]), in superconducting films [9], and superconducting rings interrupted by thin regions of insulator (called Josephson weak links) [10–13]. However, experimental verification of the Kibble-Zurek proposal has been lacking in what is arguably the simplest system—superconducting rings without Josephson weak links—because it was experimentally difficult to determine the presence or absence of single flux quanta in superconducting rings. Recent advances in magnetic microscopy techniques have now made such measurements routine.

In superconductors, an electromagnetic field adds to the scalar order parameter field because of the electrically charged Cooper pairs, causing novel effects, including fractional vortices in systems involving intrinsic or extrinsic shifts in the quantum mechanical phase [14,15]. In collaboration with C. C. Tsuei, we (Kirtley and Tafuri) used a scanning SQUID microscope to image a number of rings after repeated cooling in various magnetic fields and cooling rates to determine the probability of spontaneous fluxoid generation [16]. We showed that a second mechanism prevailed, in which the final density of fluxoids depended on a balance between thermal generation and the relaxation rates of fluxoids [17–19]. We argued that the thermal fluctuation mechanism is complementary to the “causal” mechanism and should be considered in attempts to understand phase transitions, both in the laboratory and in the early universe.

These experiments were done on rings with parameters that favored the thermal activation mechanism over the causal (Kibble-Zurek) mechanism. In their work, Monaco et al. study rings that are made of a different material and are narrow enough to suppress the thermal mechanism. They chose an experimental geometry in which the final fluxoid state of a single test ring could be determined by detecting the suppression in the critical current of a Josephson junction placed next to the ring. This, along with a carefully chosen thermal conductivity between the ring and the thermal bath, allowed rapid multiple heating and quenching cycles of the ring with varying quenching rates. Monaco et al. found that the probability of spontaneous fluxoid generation in the ring followed the expected power law in quenching rate, but the exponent $σ$ was close to $1 / 2$ , a factor of $2$ larger than the standard Kibble-Zurek prediction. Monaco et al. attribute their finding of a much weaker dependence on cooling rate than theory to the fact that they are studying a small ring: since the ring’s circumference is much smaller than the coherence length at the temperature at which the fluctuations are frozen in, the kinks are more effectively annihilated. Rings with a circumference that is large relative to the coherence length would, in this view, have the Kibble-Zurek exponent of $1 / 4$ . This explains not only their results on rings without Josephson weak links, but may also explain previous results on annular junctions, which also showed the same exponent. It remains to be seen whether these new insights about phase transitions in superconducting rings are relevant to cosmological phase transitions.

The spontaneous formation of topological defects remains a stimulating problem common to diverse fields of physics and various types of phase transitions. What is most fascinating about the class of condensed matter experiments that were inspired by cosmology is the possibility of reading their memories—the information that was frozen into the topological defects at the time they were formed.

References

R. Monaco, J. Mygind, R. J. Rivers, and V. P. Koshelets, Phys. Rev. B 80, 180501 (2009)
T. W. B. Kibble, J. Phys. A 9, 1387 (1976)
T. W. B. Kibble, Phys. Today 60, No.9, 47 (2007)
W. H. Zurek, Nature 317, 505 (1985)
P. C. Hendry, N. S. Lawson, R. A. M. Lee, P. V. E. McClintock, , and C. D. H. Williams, Nature 368, 315 (1994)
M. E. Dodd, P. C. Hendry, N. S. Lawson, P. V. E. McClintock, and C. D. H. Williams, Phys. Rev. Lett. 81, 3703 (1998)
C. Bäuerle, Yu. M. Bunkov, S. N. Fisher, H. Godfrin, and G. R. Pickett, Nature 382, 332 (1996)
V. M. H. Ruutu, V. B. Eltsov, A. J. Gill, T. W. B. Kibble, M. Krusius, Yu. G. Makhlin, B. Plaçais, G. E. Volovik, and Wen Xu, Nature 382, 334 (1996)
R. Carmi and E. Polturak, Phys. Rev. B 60, 7595 (1999)
R. Carmi, E. Polturak, and G. Koren, Phys. Rev. Lett. 84, 4966 (2000)
E. Kavoussanaki, R. Monaco, and R. J. Rivers, Phys. Rev. Lett. 85, 3452 (2000)
R. Monaco, J. Mygind, and R. J. Rivers, Phys. Rev. Lett. 89, 080603 (2002)
R. Monaco, J. Mygind, and R. J. Rivers, Phys. Rev. B 67, 104506 (2003)
C. C. Tsuei and J. R. Kirtley, Rev. Mod. Phys. 72, 969 (2000)
F. Tafuri and J. R. Kirtley, Rep. Prog. Phys. 68, 2573 (2005)
J. R. Kirtley, C. C. Tsuei, and F. Tafuri, Phys. Rev. Lett. 90, 257001 (2003)
M. Hindmarsh and A. Rajantie, Phys. Rev. Lett. 85, 4660 (2000)
M. Ghinovker, B. Ya. Shapiro, and I. Shapiro, Europhys. Lett. 53, 240 (2001)
M. Donaire, T. W. B. Kibble, and A. Rajante, New J. Phys. 9, 148 (2007)

About the Authors

John R. Kirtley received his B.A. in 1971 and his Ph.D. in 1976, both in physics, from the University of California, Santa Barbara. After a post-doctoral position at The University of Pennsylvania, he joined IBM’s Thomas J. Watson Research Center in 1978, where he remained until becoming a Research Staff Member Emeritus in 2006. He is now a consulting professor in the Applied Physics Department at Stanford University. In 1998 he shared the Oliver E. Buckley prize in condensed matter physics with C. C. Tsuei, D. J. van Harlingen, and D. M. Ginsberg. He is a fellow of the American Physical Society and of the American Association for the Advancement of Science, won the Humboldt Forschungspreis in 2007, was a Jubileum Professor at Chalmers University in Sweden the same year, and will hold a Chair d’Excellence from the CNR in Grenoble, France, 2010–2013.

Francesco Tafuri received his Ph.D. in physics at the University of Napoli “Federico II” in 1993, carrying out part of his research activity at Stony Brook University. Since 1994 he has been at the Second University of Napoli, first as an Assistant Professor and, since 2002, as Associate Professor. In 2001, he was a visiting scientist at the IBM’s Thomas J. Watson Research Center. Most of his experimental work has focused on the study of the Josephson effect and macroscopic quantum phenomena in superconductors with a high critical temperature and vortex matter in unconventional systems and oxide nanostructures.