There and back again: from magnets to superconductors

A. J. Schofield

Viewpoint

There and back again: from magnets to superconductors

School of Physics and Astronomy, The University of Birmingham, Birmingham, B15 2TT, UK

November 9, 2009• Physics 2, 93

A theory of novel phase formation near quantum critical points suggests that large fluctuations lead to magnetic analogs of inhomogeneous superconductivity.

Figure caption — **Figure 1:** There are many parallels between superconductivity and forms of magnetism. (a) The FFLO state is a superconductor where the phase of the Cooper-pair wave function varies in space periodically. (b) Conduit *et al.* find that ferromagnetic fluctuations can favor a magnetic analog of the inhomogeneous FFLO state where the spin orientation varies in space. A simple $s$ -wave superconductor (c) has the same Cooper-pair phase around the Fermi surface and is analogous to the simple ferromagnet which has an excess of, say, up spin around the Fermi surface (d). More exotic superconductors like the $d$ -wave state (e) where the Cooper-pair phase changes sign around the Fermi surface are often stabilized near quantum critical points. Their corresponding magnetic states—like the spin nematic (f) where the excess spin direction changes sign around the Fermi surface—might also compete for stability.

Interactions often modify the behavior of quantum particles and reorganize them into new phases of matter. One dramatic example is the superconducting state, where electrons with attractive interactions form Cooper pairs. The most pertinent interactions in metals are often effective ones—mediated by lattice vibrations and magnetism—and they can be altered by changing the electron environment. Changes to chemical composition, applying magnetic fields and or pressure have the most dramatic effect on the interactions near a so-called quantum critical point [1]. This is the point in the phase diagram where, at zero temperature, a metal is just on the verge of developing magnetic order. In this vicinity electrons interact via intense quantum and thermal fluctuations of that incipient order. Those long-range interactions both modify the metallic properties and also lead to new low-temperature phases such as superconductivity. In a paper in Physical Review Letters [2], Gareth Conduit and Ben Simons at the Cavendish Laboratory in Cambridge and Andrew Green at the School of Physics and Astronomy at St. Andrews, both in the UK, undertake a theoretical study of metals near a ferromagnetic quantum critical point. They show that critical fluctuations there can favor a low-temperature phase that is the magnetic analog of a superconducting state.

That superconductivity should occur near quantum criticality is a surprise; the usual “rule” is that superconductivity and magnetism do not mix [3]. That said, there are now many examples of superconductivity in quantum critical metals [4]. It seems that the magnetic fluctuations drive the superconductivity by acting as the “glue” that binds the Cooper pairs. Calculations suggest that such Cooper pairs form with an internal angular momentum—distinct from conventional $s$ -wave superconductors [5].

But is superconductivity the only new phase of matter that emerges near a quantum critical point? Apparently not, for there are a number of examples of nonsuperconducting phase transitions appearing in quantum critical metals where the underlying nature of the new phase is mysterious. One of the clearest cases is seen in ${Sr}_{3} {Ru}_{2} O_{7}$ (see Ref. [6]). This material is on the cusp of ferromagnetism, and can be tipped over the edge by an applied magnetic field and tuned to quantum criticality by varying the direction of the field. But its quantum critical point is preempted by a novel phase. One of the motivations for the Letter by Conduit et al. is to study the identity and formation mechanism of this phase.

Metals on the border of ferromagnetism have an unexpected richness because the critical magnetic fluctuations are accompanied by other soft modes [7]. Diagrammatic perturbation theory—the usual starting point for the study of these quantum critical metals—leads to nonanalytic terms [8] that significantly modify the conventional treatment [9]. In effect, they generate attractive interactions between magnetic fluctuations that may force the ferromagnetic phase transition to become first order at low temperatures [10]. But could they also promote other types of order?

Conduit et al. address this question with two methods, both of which make certain assumptions concerning the order. The authors are motivated by suggestions that a spiral order could preferentially develop [11–13]. In contrast to a ferromagnet where the spins align in the same direction everywhere, in a spiral state the spins form a twisted pattern that repeats over a characteristic length. First, they use perturbation theory techniques that include the critical and the soft modes to calculate the free energy and thereby to find the most energetically favored state. This method seems significantly simpler than previous diagrammatic methods. Second, they perform a numerical quantum Monte Carlo calculation that is nonperturbative with a trial wave function, which also allows a magnetic spiral phase to emerge. In both approaches they find that the expected first-order transition to a uniform ferromagnet is masked at low temperature by an energetically favorable spiral phase. It is a fascinating suggestion that will lead to further experimental inquiry.

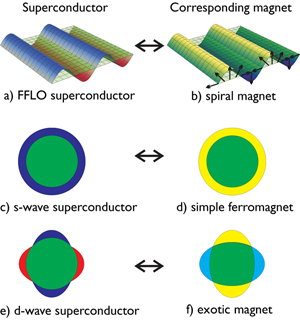
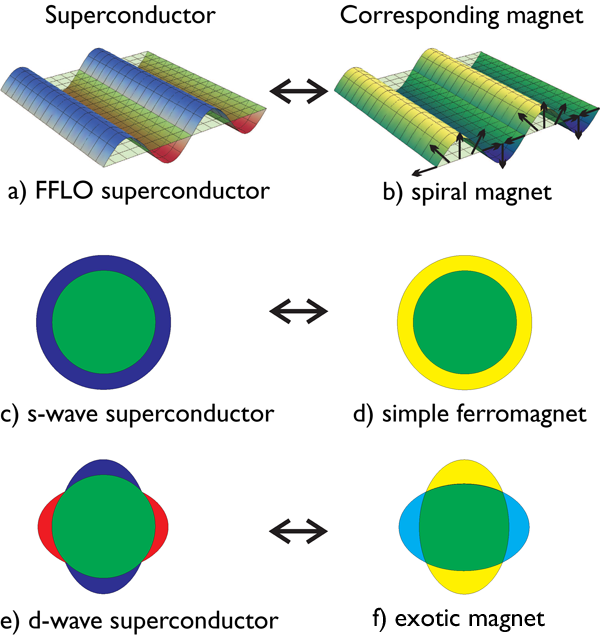
The authors also note a similarity between the emergence of their spiral magnetic state and earlier work predicting inhomogeneous superconductivity—the Fulde-Ferrel-Larkin-Ovchinnikov (FFLO) state [14,15] (Fig. 1). In the FFLO state, the phase of the Cooper-pair wave function develops a periodic pattern in space with a characteristic wavelength signifying Cooper pairs with center-of-mass momentum. This connection suggests a more profound link between the emergence of superconductivity at quantum critical points and the identity of the mysterious new phases seen in some quantum critical metals. Superconductivity is formed from electron-electron pairs around the Fermi surface. Magnetism results from electron-hole pairs as the electron fluid reorganizes itself. The similarity indicates a general mapping between novel superconductors and different types of magnetic order. For example, the simple ferromagnet with its excess of majority-spin electrons and minority-spin holes distributed isotropically around the Fermi surface would be the magnetic version of a conventional $s$ -wave superconductor. The textured magnetic state that Conduit et al. find is the magnetic analog of the FFLO state where now particle-hole rather than Cooper pairs have center-of-mass momentum. So, just as quantum critical fluctuations can induce pairing in the Cooper (particle-particle) channel to make superconductors, Conduit et al. show that quantum critical fluctuations can also favor “pairing” in the magnetic or particle-hole channel.

But why should nature stop at the magnetic version of the FFLO phase? Could these mysterious phases appearing in the presence of critical fluctuations be more general magnetic analogs of possible exotic superconductors [16]? We have already seen that quantum critical fluctuations favor Cooper pairs with internal angular momentum— $p$ -wave and $d$ -wave superconductors—where the phase of the Cooper pair varies around the Fermi surface. These superconductors also have associated magnetic counterparts. They correspond to Pomeranchuk distortions, where the magnetic density varies in momentum space around the Fermi surface [17]. In the strong coupling limit this leads to a spin-nematic electron liquid—a state with broken rotational symmetry but without a periodic texture [18].

Alternatively, one could start with the mixed state of the superconductor in a magnetic field and ask what its magnetic counterpart would look like. The answer turns out to be an unusually textured magnet [19] that was recently observed in $MnSi$ [20].

As this last example shows, experiment will be the final arbiter of which new phases will be preferred near quantum criticality. In ${Sr}_{3} {Ru}_{2} O_{7}$ the experimental evidence for a nematic state is quite strong and supported by mean-field calculations (see references in Ref. [6]) as well as a recent fluctuation study [21]. However, inelastic neutron scattering experiments suggest that there are features at finite wavelength [22], and the state proposed by Conduit et al. should be readily visible in elastic neutron scattering. Even if not in ${Sr}_{3} {Ru}_{2} O_{7}$ , the growing number of quantum critical materials gives ample scope for a fluctuation-driven magnetic analog of superconducting states to be realized.

References

P. Coleman and A. J. Schofield, Nature 433, 226 (2005); H. v. Löhneysen, A. Rosch, M. Vojta, and P. Wölfle, Rev. Mod. Phys. 79, 1015 (2007)
G. J. Conduit, A. G. Green, and B. D. Simons, Phys. Rev. Lett. 103, 207201 (2009)
R. A. Hein, R. L. Falge, B. T. Matthias, and C. Corenzwit, Phys. Rev. Lett. 2, 500 (1959)
N. D. Mathur, F. M. Grosche, S. R. Julian, I. R. Walker, D. M. Freye, R. K. W. Haselwimmer, and G. G. Lonzarich, Nature 394, 39 (1998)
P. Monthoux, D. Pines, and G. G. Lonzarich, Nature 450, 1177 (2007)
A. W. Rost, R. S. Perry, J.-F. Mercure, A. P. Mackenzie, and S. A. Grigera, Science 325, 1360 (2009) and references therein
D. Belitz, T. R. Kirkpatrick, and T. Vojta, Rev. Mod. Phys. 77, 579 (2005)
D. J. W. Geldart and M. Rasolt, Phys. Rev. B 15, 1523 (1977)
D. Belitz, T. R. Kirkpatrick, and T. Vojta, Phys. Rev. B 55, 9452 (1997)
D. Belitz and T. R. Kirkpatrick, Phys. Rev. Lett. 89, 247202 (2002)
J. R. Rech, C. Pépin, and A. V. Chubukov, Phys. Rev. B 74, 195126 (2006)
D. V. Efremov, J. J. Betouras, and A. Chubukov, Phys. Rev. B 77, 220401 (2008)
A. M. Berridge, A. G. Green, S. A. Grigera, and B. D. Simons, Phys. Rev. Lett. 102, 136404 (2009)
P. Fulde and R. A. Ferrell, Phys. Rev. 135, A550 (1964)
A. I. Larkin and Y. N. Ovchinnikov, JETP 20, 762 (1965)
G. G. Lonzarich (about 1996), private communication
A. F. Ho and A. J. Schofield, EPL 84, 27007 (2008)
S. A. Kivelson, E. Fradkin, and V. J. Emery, Nature 393, 550 (1998)
A. N. Bogdanov and D. A. Yablonskii, JETP 68, 101 (1989)
S. Muhlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, and P. Boni, Science 323, 915 (2009)
A. V. Chubukov and D. L. Maslov, arXiv:0908.4433
S. Ramos, E. M. Forgan, and C. Bowell et al., Physica B 403, 1270 (2008)

About the Author

Andy Schofield graduated from the University of Cambridge in 1989 with a B.A. and in 1993 with a Ph.D. He was a postdoc at Rutgers, NJ (1994–1996), a Royal Society University Research Fellow at Cambridge, and moved to the University of Birmingham in 1999 where he is now Professor of Theoretical Physics. His research interests are in the theory of strongly correlated quantum systems.