Islands of insight in the nuclear chart

B. Alex Brown

Viewpoint

Islands of insight in the nuclear chart

B. Alex Brown

Michigan State University, East Lansing, MI 48824, USA

December 13, 2010• Physics 3, 104

A one of a kind radioactive beam experiment yields new insight for neutron-rich nuclei.

Figure caption — **Figure 1:** Nuclear chart showing the stable nuclei (black) and those predicted to lie inside the proton and neutron drip lines (open blue). The archipelago of islands where the shell-model magic numbers are broken is shown in red. The nuclei $^{30} Mg$ and $^{32} Mg$ involved in this experiment are shown in green, with their shell-model structure for neutrons in the upper left-hand corner.

Like the shell model for atoms, which identifies which elements are volatile and which are inert, the nuclear shell model has guided our understanding of nuclear properties. Certain “magic number” landmarks associated with “inert” nuclei have dominated the nuclear landscape for over 50 years. As the more exotic neutron-rich nuclei are being studied, however, one finds that nuclear properties associated with the traditional landmarks can suddenly disappear. The reason is that both the relative importance of the average (“mean field”) and residual nuclear interactions, as well as the mean field itself, change.

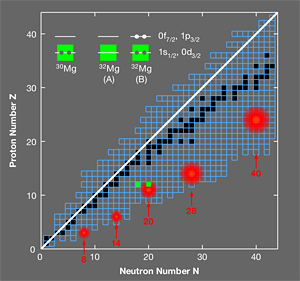
One of the regions of the chart of nuclides where this breakdown occurs is at $N = 20$ ( $N$ is the number of neutrons) and it is called the “island of inversion” (Fig. 1). The island of inversion is now known to be part of an archipelago of “islands of shell breaking” associated with the magic neutron numbers $8$ , $14$ , $20$ , $28$ , and $40$ . In order to accurately account for the effects of interactions and understand how the shell model breaks down, theorists need high-precision spectroscopic data for the isotopes in these regions. Now, in a paper appearing in Physical Review Letters, an international collaboration (Wimmer et al.) presents precise spectroscopic measurements of the neutron-rich element magnesium- $32$ , which lies in the much explored island of inversion at $N = 20$ [1]. The measurements, which are the first of their kind and were performed at the REX-ISOLDE radioactive beam facility at CERN, address a long standing question about the low-lying energy spectrum of this nucleus and provide important information about the collective effects of nuclear interactions.

A Google search for “island of inversion” yields about $1000$ results, almost all of which refer to a group of neutron-rich nuclei in a region of the nuclear chart centered around sodium- $31$ , which has $11$ protons and $20$ neutrons (stable sodium has $12$ neutrons). The term goes back to a paper by Warburton, Becker, and Brown [2] in which they studied the unusual features for nuclei in this mass region with the nuclear shell model. The magic numbers quoted above are derived from the nuclear shell model, the foundation of which is the appearance of gaps in the spectrum of single-particle energies that arise from the average (mean-field) interaction of one nucleon with all of the other nucleons. To draw an analogy with atomic physics, like the highly stable elements with closed electronic orbitals, the single-particle energy levels of “magic number” nuclei are filled with protons or neutrons (fermions that obey the Pauli principle) up to an energy just below the gaps. The energies of the first excited states in the nuclei with magic numbers are relatively high compared with those of neighboring nuclei since a proton or neutron must be excited to states across the gap. In contrast, inside the “islands of shell breaking” the energy of the first excited state drops and no longer shows any indication of the magic numbers found for the nuclei closer to stability. This archipelago holds the secret to many puzzling microscopic features of nuclear structure.

Current experiments with radioactive beams of isotopes are concentrated on studying the properties of neutron-rich nuclei out to the neutron drip line (the bottom-right edge of the chart of nuclei), where the islands of inversion lie. Inside the neutron drip line, the nuclei beta decay toward stability with lifetimes characteristic of the weak interaction, on the order of $10^{- 3}$ seconds. With this long lifetime, the masses, excited states, and decay properties of these nuclei can be studied in some detail when they can be produced. Beyond the neutron drip line, the nuclei are unstable to neutron decay and have a lifetime characteristic of the strong interaction, on the order of $10^{- 20}$ seconds. The experimental study of these nuclei is limited to observation of the neutrons from their decay.

With these general remarks in mind, one can look at the region of the nuclear chart probed by the REX-ISOLDE experiment. Two configurations for magnesium- $32$ are displayed for $20$ neutrons (Fig. 1, upper left); the closed-shell configuration A, and configuration B consisting of two neutrons excited from the $0 d_{3 / 2}$ and $1 s_{1 / 2}$ orbitals into the $0 f_{7 / 2}$ and $1 p_{3 / 2}$ orbitals across the $N = 20$ shell gap, making a two-particle, two-hole state. Near the shell gaps, configurations of type B usually appear as excited states and are sometimes called pairing vibrations. The energy of these states is lower than twice the shell gap due to the pairing correlations between the particles and between the holes.

In this island of inversion, configurations of the type B become the ground state rather than the excited state. This change is sudden, with B forming an excited state in silicon- $34$ ( $20$ neutrons and $14$ protons) and then becoming the ground state for magnesium- $32$ ( $20$ neutrons and $12$ protons). Two factors contribute to this sudden change: a gradual reduction in the spherical $N = 20$ shell gap as one approaches the neutron drip line at fluorine ( $9$ protons), and the configuration for the protons suddenly changing from “closed shell” in silicon- $34$ to “open shell” in magnesium- $32$ , which leads to stronger proton-neutron correlations and deformation.

Many experiments have studied the states in the island of inversion with configurations similar to B. The work at REX-ISOLDE provides the first confirmation that the predicted coexisting excited state A exists and shows some of its properties, providing a much sought after example of an explicit disappearance of shell closure. It is the first experiment of its type where a radioactive beam of magnesium-30 reacts with a target loaded with radioactive tritium. Two neutrons from the tritium target are transferred to magnesium- $30$ , leaving magnesium- $32$ and a proton that is detected. The shell-model configuration of magnesium- $30$ is shown in Fig 1. When two neutrons are added to make a final state with spin and parity $J^{π} = 0^{+}$ , they can go into the $0 d_{3 / 2}, 1 s_{1 / 2}$ orbitals, making state A, or into the $0 f_{7 / 2}, 1 p_{3 / 2}$ orbitals, making state B. (The labels $n ℓ_{j}$ here are those associated with a wave function from a spherical potential with radial quantum number $n$ , orbital quantum number $ℓ$ , and total angular momentum $j$ ). The REX-ISOLDE team observed two $0^{+}$ states: the ground state and an excited state at $1.06 MeV$ . The energy of the excited state, which is presumed to correspond to configuration A, is lower than any of the theoretical predictions discussed in this paper. The simplest estimate based on the theoretical extrapolation for the energy of A together with the measured energy of the ground state B is $2.3 MeV$ [3]. Understanding the reason for this disagreement with theory will be crucial for improving the many-body models as they are used to predict the properties of nuclei in even more neutron-rich nuclei.

The cross sections for the population of these two states give indirect information on the details of their structure. It is inferred that there is mixing between A and B, and that the $1 p_{3 / 2}$ component of B is larger than expected. This may be a signal that the single-particle energy of the $1 p_{3 / 2}$ orbital, which is about one $MeV$ above that of the $0 f_{7 / 2}$ orbital in $^{34} Si$ , is dropping relative to $0 f_{7 / 2}$ as one approaches the neutron drip line. This is a feature of loosely bound orbitals with $ℓ = 1$ [4] and may be important for understanding why the neutron drip line suddenly changes from $1$ 6 neutrons for the oxygen isotopes ( $8$ protons) to greater than $22$ neutrons for the fluorine isotopes ( $9$ protons).

With the advent of experiments like the one reported by the REX-ISOLDE collaboration, the likes of which were inconceivable even a few years ago, we are beginning to gain a deeper understanding of the complexity of the collective effects that shape the nuclear landscape. The reasons for the existence of the islands of shell breaking are complex, and much needs to be explored. In addition, new magic numbers may appear near the neutron drip line [5] (for example, $^{24} O$ shows evidence that $N = 16$ is a magic number). Apart from problems of intrinsic interest to nuclear physics, several questions in astrophysics also hinge crucially on our understanding of nuclear stability. Ultimately, an important goal is to be able to confidently predict the properties of neutron-rich nuclei and their role in the stellar nucleo-synthesis of elements. Such an objective will require a coherent program of theoretical, computational, and experimental advances.

References

K. Wimmer et al., Phys. Rev. Lett. 105, 252501 (2010)
E. K. Warburton, J. A. Becker, and B. A. Brown, Phys. Rev. C 41, 1147 (1990)
B. A. Brown and W. A. Richter, Phys. Rev. C 74, 034315 (2006)
I. Hamamoto, Phys. Rev. C 76, 054319 (2007)
T. Otsuka, R. Fujimoto, Y. Utsuno, B. A. Brown, M. Honma, and T. Mizusaki, Phys. Rev. Lett. 87, 082502 (2001)

About the Author

Alex Brown is a Professor in the Department of Physics and Astronomy at Michigan State University and a member of the nuclear theory group at the National Superconducting Cyclotron Laboratory. His research focuses on theoretical models for nuclear structure and their applications to experiments with rare isotope beams, nuclear astrophysics, and fundamental symmetries in the nucleus. He received his Ph.D. in 1974 from Stony Brook University. In 2008 he was recognized as an Outstanding Referee by the American Physical Society.