Generation of light bullets
Researchers have long sought to generate wave packets that are localized in all three dimensions (3D) as they propagate in space or evolve in time. Such wave packets theoretically exist in settings as diverse as condensed-matter physics, degenerate quantum gases, and nonlinear optics, but experimental observations are extremely rare. In a recent paper in Physical Review Letters, Stefano Minardi and co-workers at Friedrich Schiller University in Jena, Germany, report the generation of spatiotemporal solitons or “light bullets”—localized packets of electromagnetic energy that propagate without spreading out, despite diffraction and dispersion [1]. In addition to its intrinsic scientific interest, the study of spatiotemporal solitary waves should lead to ways to enhance light-matter interactions as well as to powerful optical information-processing systems.
Diffraction causes light beams to spread in the transverse direction as they propagate. A temporal pulse of light analogously spreads out owing to material dispersion: the index of refraction varies with wavelength, so the different wavelengths that make up the pulse move at different speeds. Dispersion can be normal or anomalous. With normal dispersion, low frequencies move faster than high frequencies in a pulse (“red leads blue”), while with anomalous dispersion, the high frequencies lead the low frequencies. Thus a pulsed beam spreads in both time and space as it propagates.
However, nonlinear effects can counteract the spreading. The index of refraction typically increases with the intensity of a light beam. A beam with a Gaussian-shaped transverse intensity profile (which is what lasers usually produce) will undergo self-focusing as its center picks up a larger phase than its edges, as would occur in a positive lens. Self-focusing can nominally balance diffraction, to make a stable beam of fixed size. In the time domain, the intensity-dependent refraction can balance the effects of anomalous material dispersion to make a pulse that propagates indefinitely without spreading out. Stable localized wave packets that balance nonlinear and linear effects in these ways are called solitons. They are remarkable because either the linear or the nonlinear effects acting alone would cause the pulse or beam to decay, but in the right combination they lead to waves that propagate without spreading. Temporal solitons in optical fibers are of great interest as bits of information in telecommunications, for example.
Silberberg suggested that it might be possible for a self-focusing nonlinearity to compensate both spatial and temporal spreading of a light pulse. The resulting packet of energy is a spatiotemporal soliton [2], which is referred to as a “light bullet” in recognition of its particlelike nature. However, spatiotemporal solitons are unstable in ordinary materials such as glass; a precise balance of the nonlinear and linear effects is required, so the slightest variation of pulse or material parameters destroys the wave packet. Over the past 20 years, researchers have explored a variety of alternative materials and techniques to generate light bullets. The first optical spacetime solitons were reported in 1999, but those had only one of the two transverse dimensions controlled—the beam was in the shape of a long narrow ellipse [3]. So-called X waves have profiles with long tails that accompany the main hump. These resist the effects of diffraction and dispersion to some extent [4] but are not localized.
The propagation of light waves in media with properties that are modulated in the transverse dimension has also received much attention in the past two decades. The simplest example of this would be a one-dimensional array of parallel optical waveguides, which are close enough that their evanescent fields overlap. That overlap can couple energy from one waveguide to its neighbors. Thus light injected into a waveguide will eventually transfer to the other waveguides in the array, in a process that can be thought of as discrete diffraction. Arrays of waveguides can be engineered to control the sign and magnitude of this diffraction [5].
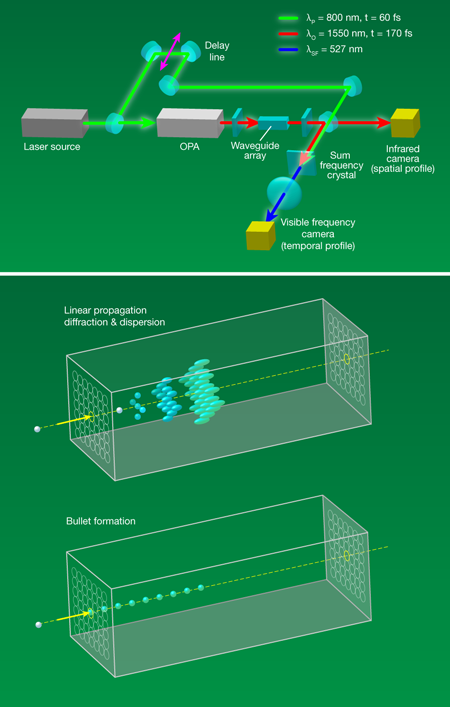
Minardi et al. exploit discreteness to stabilize the 3D light bullets, which had been considered theoretically [6]. These workers fabricated a two-dimensional hexagonal array of silica glass waveguides (Fig. 1). The waveguides are 40mm long and 10μm in diameter, and each one is 33μm from its nearest neighbors. Fabrication of such arrays with the precision needed for demanding experiments on nonlinear wave propagation was only developed recently. Experiments were performed by launching 170- fs pulses at 1550- nm wavelength into a single waveguide in the center of the array, and recording the spatial and temporal profiles of the pulses at the output end of the structure. At this wavelength, the glass has anomalous dispersion. Measurements are compared to numerical solutions of the coupled nonlinear wave equations that govern pulse propagation in the array, and the agreement between experiment and calculations is very good.
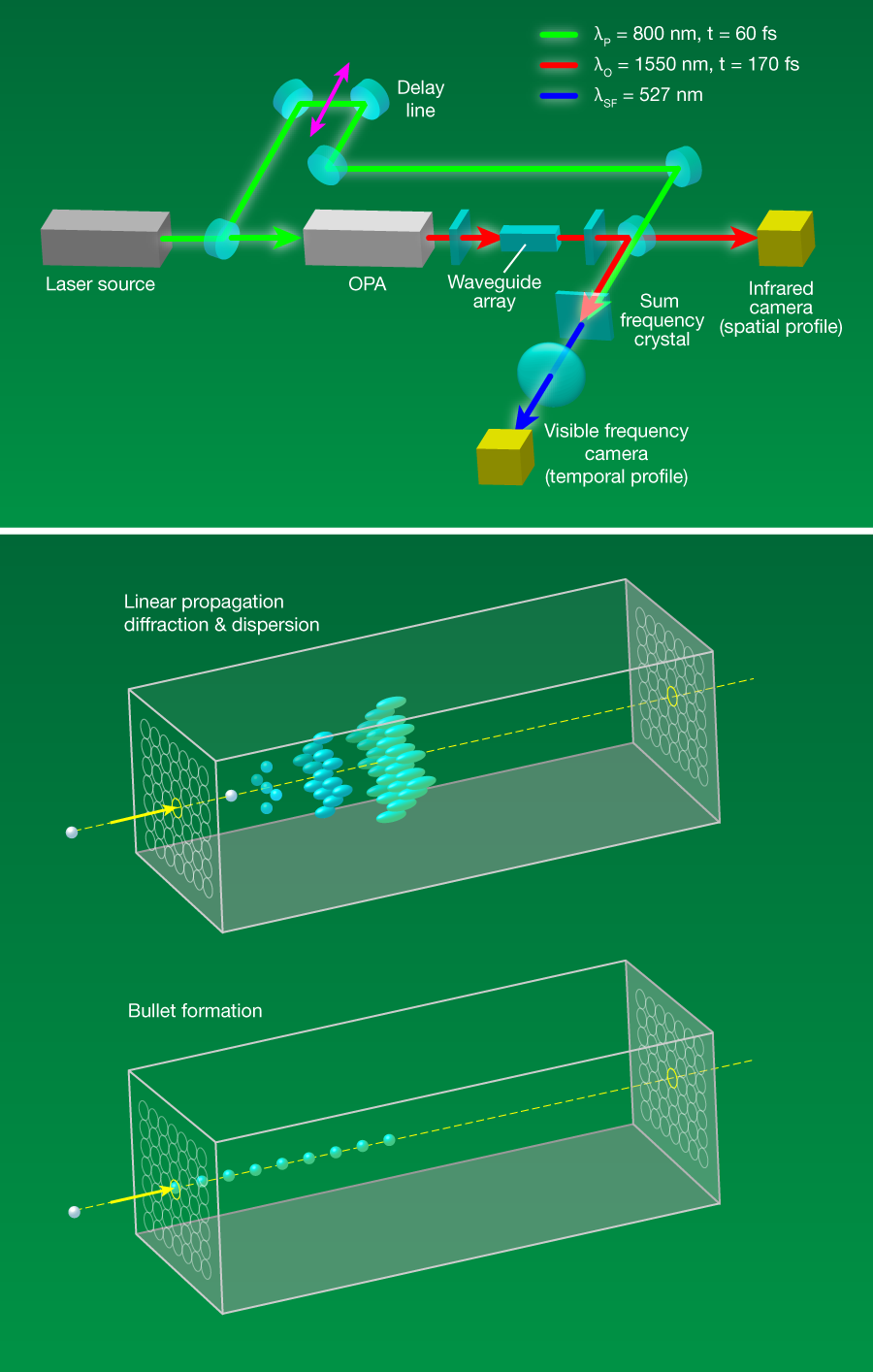
Experiments with low-power input pulses exhibit the linear propagation of light in the array and thus serve as the control. Light spreads from the original waveguide into the neighboring waveguides and the pulse profile broadens, as expected, given the magnitudes of discrete diffraction and dispersion, respectively. When the peak power of the input pulse is increased to about 1 megawatt, the light becomes localized in the original waveguide and the output pulse duration is much shorter than at low power (see Fig. 1). We can think of this as discrete self-focusing: the coupling between waveguides is changed by the high intensity. Simultaneously, a temporal soliton is forming by the balance of nonlinear refraction and anomalous dispersion. Intuitively, the bullet can be thought of as a temporal soliton that stays in one waveguide. Of course, the spatial and temporal evolutions are coupled because these processes influence each other. By comparing the experimental observations to the results of numerical simulations, the researchers conclude that the light bullets propagate stably in the interior of the array. The spatial profile is stationary for about twice as far as it would be in linear propagation, and the temporal profile is stationary for about 9 times as far as it would be in linear propagation. These are the first light pulses to be spatially and temporally localized for distances longer than the characteristic lengths of linear propagation.
Although the array of waveguides supports the stable light bullets, it also contributes to their eventual decay in the experiments of Minardi et al. Higher-order effects such as Raman scattering lead to a redshift of the pulse spectrum in propagation. The coupling between adjacent waveguides is quite sensitive to the wavelength, so the balance of linear and nonlinear processes is upset by the shift of the spectrum, and the light bullets decay abruptly.
Despite concerted efforts in the optical physics community, the generation of light bullets had been elusive until the report by Minardi and co-workers. Their work is a major step forward as the first demonstration of nonlinear propagation of a 3D localized optical wave packet. However, much remains to be done. It will be desirable to study bullet propagation over longer distances, as well as the interactions of light bullets. This work will presumably stimulate efforts to generate light bullets in other settings. Understanding of light bullets that is developed in this and future work will be relevant to other nonlinear phenomena, such as optical rogue waves, for example. In addition to the scientific interest in light bullets, such pulses offer potential for ultrafast optical digital logic, with switching rates of several terahertz, in the future [7].
References
- S. Minardi, F. Eilenberger, Y. V. Kartashov, A. Szameit, U. Röpke, J. Kobelke, K. Schuster, H. Bartelt, S. Nolte, L. Torner, F. Lederer, A. Tünnermann, and T. Pertsch, Phys. Rev. Lett. 105, 263901 (2010)
- Y. Silberberg, Opt. Lett. 22, 1282 (1990)
- X. Liu, L. Qian, and F. W. Wise, Phys. Rev. Lett. 82, 4631 (1999)
- P. Di Trapani et al., Phys. Rev. Lett. 91, 093904 (2003)
- F. Lederer et al., Phys. Rep. 463, 1 (2008)
- A. Aceves et al., Opt. Lett. 19, 329 (1994); L. Berge, Phys. Rep. 303, 259 (1998); D. Mihalache et al., Phys. Rev. E 70, 055603 (2004)
- R. Macleod, K. Wagner, and S. Blair, Phys. Rev. A 52, 3254 (1995)