How to turn a topological insulator into a superconductor

Noah Bray-Ali; Stephan Haas

Viewpoint

How to turn a topological insulator into a superconductor

Noah Bray-Ali

Department of Physics & Astronomy, University of Kentucky, Lexington, KY 40506, USA

Stephan Haas

February 1, 2010• Physics 3, 11

By doping the topological insulator bismuth selenide with copper to form copper layers, a topological superconductor is created.

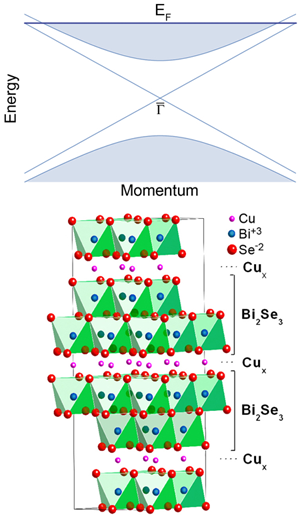
Figure caption — **Figure 1:** (Top) Idealized surface dispersion for doped topological insulator ${Cu}_{x} {Bi}_{2} {Se}_{3}$ . Shaded area corresponds to occupied bulk modes. Linearly dispersing surface modes meet at the time-reversal invariant momentum $k = 0$ . (Bottom) Crystal structure of ${Cu}_{x} {Bi}_{2} {Se}_{3}$ , showing intercalated copper layers.

Topological insulators are materials with a bulk electronic band gap and gapless, delocalized, surface states [1–3]. One such compound, bismuth selenide ( ${Bi}_{2} {Se}_{3}$ ), has received particular attention recently because it has a large band gap and a relatively simple surface band structure containing a single Dirac fermion mode with a lightlike, linear dispersion [4] (Fig. 1, top). This Dirac metal forms a conducting channel that is believed to be topologically protected by time-reversal symmetry, and hence robust to disorder, interactions, and thermal fluctuations, potentially leading to room-temperature device applications [5]. At an interface with a conventional superconductor, the surface modes of the topological insulator have been predicted to rearrange in an interesting fashion [6]. For example, in the region of the insulator underneath the core of a vortex excitation in the superconductor, the gapless surface modes may combine to create a Majorana fermion, a collective excitation that is its own antiparticle and is the basic element in a recent proposal for fault-tolerant quantum computing [7].

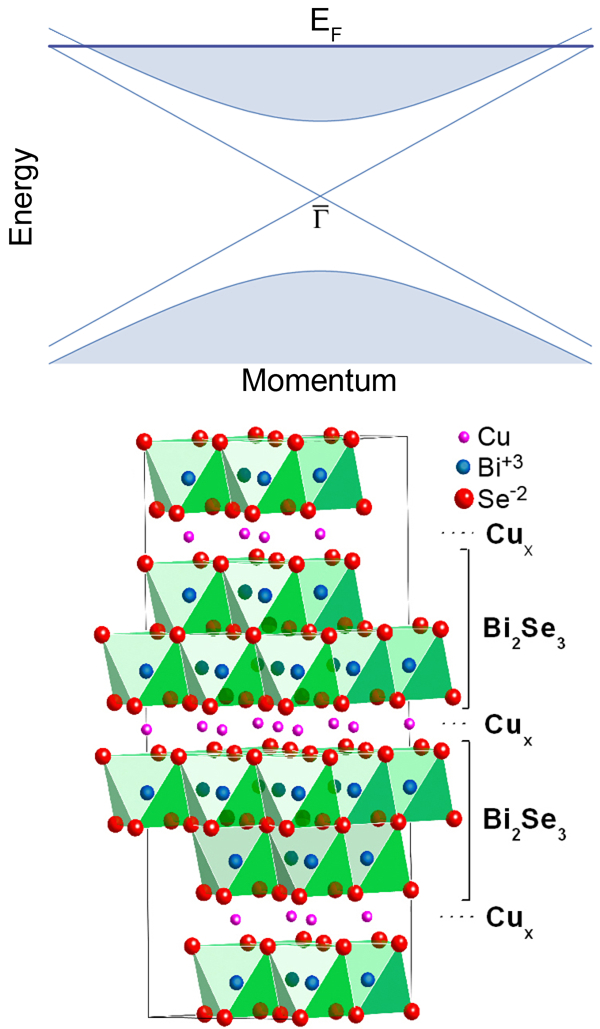
A new direction in the research on these materials is indicated in a recent publication by Yew San Hor and collaborators at Princeton University, US, and Delft Institute of Technology, in the Netherlands, who report in Physical Review Letters that, under certain conditions, topological insulators become superconducting [8]. This raises the possibility of creating a high-quality interface between a superconductor and a topological insulator, since the structural properties of the new superconductor are nearly identical to its parent insulator (Fig. 1, bottom).The transition temperatures observed so far are roughly comparable to elemental superconductors such as tin and niobium; however, while the transition temperatures may be similar, to make bismuth selenide superconduct requires the introduction of a large concentration of copper dopants.

Native bismuth selenide is a layered compound with rather weak van der Waals couplings between the layers. When doping this material with copper, the copper atoms can behave in two different ways with significant consequences. The copper either enters the $BiSe$ layers as substitutions for bismuth, in which case the result is a nonsuperconducting compound ${Bi}_{(2 - x)} {Cu}_{x} {Se}_{3}$ . If, however, the copper atoms populate the interlayer gaps, the resultant structure is copper-intercalated bismuth selenide, ${Cu}_{x} {Bi}_{2} {Se}_{3}$ , which superconducts in the doping regime $0.1 < x < 0.15$ . Using a fine-tuned growth process, Hor et al. were able to avoid copper substitution for bismuth and thus produce relatively pure samples of ${Cu}_{x} {Bi}_{2} {Se}_{3}$ .

Superconductivity in these compounds was observed with standard resistivity and magnetization measurements that indicate a maximum transition temperature of around $4 K$ , as well as a strongly anisotropic upper critical magnetic field of about $5 T$ for fields along the weakly coupled direction, and about $2 T$ for fields parallel to the layered planes. Scanning tunneling microscopy experiments reveal that the copper atoms enter the interlayer regions in random positions, leading to a noticeable upward shift of the lattice parameter along the layer stacking direction. (Fig. 1, bottom)

The most obvious questions raised by these observations are as follows: What is the origin and nature of superconductivity in this doped topological insulator, and why does it depend so delicately on the sample preparation? The experimental evidence suggests that the intercalated copper dopants provide $n$ -type charge carriers, which effectively raise the chemical potential of the native compound into the bulk conduction band (Fig. 1 top). Remarkably, the doped compound has hundreds of times fewer carriers than metals with a comparable transition temperature, indicating that the lightlike, Dirac dispersion of the conduction band is particularly susceptible to superconductivity. However, this may not be the whole story, since copper dopants substituting for bismuth atoms within the $BiSe$ layers also provide charge carriers, but do not yield a superconductor. The clue seems to be in the structure. The intercalated copper atoms are expected to introduce less disorder into the transport within the $BiSe$ planes than copper atoms that substitute for bismuth, and this may well be the reason why copper-intercalated ${Bi}_{2} {Se}_{3}$ is superconducting, whereas substitutional ${Bi}_{(2 - x)} {Cu}_{x} {Se}_{3}$ is not. It would be interesting to see if superconductivity can be achieved in other topological insulators, such as bismuth telluride or bismuth antimonide [9,10]. Furthermore, stoichiometric, impurity-free superconductivity may be within reach by applying pressure to the undoped compounds and would address the role that the structure plays.

This discovery of superconductivity in doped ${Bi}_{2} {Se}_{3}$ also causes one to pose questions related to the topological character of the parent compound, such as the following: Does the superconductor have gapless, delocalized surface states like the topological insulator does? If the new superconductor discovered by Hor et al. has gapless surface states itself, then the interface with its parent topological insulator may be even richer than previously thought. A further possibility raised by the work of Hor et al. is that one may be able to dope topological insulators with other transition metals besides copper. Introducing magnetic impurities, such as iron, just below the surface might open up a gap in the surface states, while preserving the band structure of the bulk [11,12]. If that is the case, then the surface-doped compound would be magnetoelectric: applying a magnetic field would induce an electric dipole moment in the material and applying an electric field would create a magnetic dipole moment [11,12]. If one dopes in magnetic impurities in the bulk, not just at the surface, one could make the material antiferromagnetic. The collective excitations would then couple to light in the same way that an axion (a leading dark matter candidate posited over thirty years ago to resolve the strong CP problem) does, giving the doped compound remarkable electro-optical properties in the far-infrared regime [13].

Concretely, Hor et al. have shown that topological insulators are promising materials, and that it is possible to grow high-quality samples even with large concentrations of dopants. Further, their discovery of superconductivity in ${Cu}_{x} {Bi}_{2} {Se}_{3}$ is a surprising result at a first glance because, while neither bismuth selenide nor copper superconduct, the combination does, and yet other subtly different combinations such as ${Bi}_{(2 - x)} {Cu}_{x} {Se}_{3}$ do not. Finally, their thorough characterization of the structural, transport, and magnetization properties of this interesting material provide a firm foundation for local probes, spectroscopy, and thermodynamic measurements, and raise the possibility for development of superlattices, thin films, and devices.

Correction (4 February 2010): Ref. 3, Phys. Rev. B published paper citation added.

References

L. Fu, C. L. Kane, and E. J. Mele, Phys. Rev. Lett. 98, 106803 (2007)
J. E. Moore and L. Balents, Phys. Rev. B 75, 123106 (2007)
R. Roy, arxiv:cond-mat/0607531; Rahul Roy, Phys. Rev. B. 79, 195322 (2009)
Y. Xia et al., Nature Phys. 5, 398 (2009)
J. E. Moore, Nature Phys. 5, 378 (2009)
L. Fu and C. L. Kane, Phys. Rev. Lett. 100, 096407 (2008)
A. Kitaev, Ann. Phys. 321, 2 (2006)
Y. S. Hor, A. J. Williams, J. G. Checkelsky, P. Roushan, J. Seo, Q. Xu, H. W. Zandbergen, A. Yazdani, N. P. Ong, and R. J. Cava, Phys. Rev. Lett. 104, 057001 (2010)
Y. L. Chen et al., Science 325, 178 (2009)
D. Hsieh, Science 323,919 (2009)
X.-L. Qi, R. Li, J. Zang, and S.-C. Zhang, Science 3231184 (2009)
Andrew M. Essin, Joel E. Moore, and David Vanderbilt, Phys. Rev. Lett. 102, 146805 (2009)
R. Li et al., arXiv:0908.1537(cond-mat)

About the Authors

Noah Bray-Ali is a lecturer in the Physical Sciences Department of Mount Saint Mary’s University-Los Angeles. He earned a PhD in physics from the University of California, Berkeley, in 2006 for work on low-dimensional and strongly correlated electron systems. He then held postdoctoral positions in condensed-matter physics, quantum information science, and atomic physics. Recently, he has worked on resolving long-standing tensions and large-scale discrepancies between the standard model of particle physics and precision measurements of fundamental particle properties using accelerated particle beams in colliders and storage rings.

Stephan Haas is a condensed matter theorist with research interests in quantum information theory, quantum magnetism, and unconventional superconductivity. His research group investigates microscopic models of interacting electronic systems, using numerical techniques such as Quantum Monte Carlo to study their phase diagrams, thermodynamics, and excitation spectra. He received his Ph.D. from Florida State University, followed by a postdoc at the Swiss Federal Institute of Technology. He is currently a professor at the University of Southern California.