Going eight separate ways

Shaffique Adam

Viewpoint

Going eight separate ways

Shaffique Adam

Center for Nanoscale Science and Technology, National Institute of Standards and Technology, 100 Bureau Drive, Gaithersburg, MD 20899-6202, USA

February 8, 2010• Physics 3, 12

A very high magnetic field splits the zero-energy Landau level of bilayer graphene revealing eight distinct levels.

Figure caption — **Figure 1:** Schematic of the eightfold symmetry breaking of the zero-energy Landau level in graphene bilayers. Vertical axis is energy, while offsets in the horizontal axis are used for visual clarity.

Symmetry is at the heart of all physics. Predicting the behavior of a material by studying underlying symmetries is one of the oldest and most powerful theoretical techniques, with quite impressive consequences: the symmetry of time invariance gives rise to energy conservation while rotational symmetry underlies the conservation of angular momentum. What then if symmetry is broken? Broken symmetry often hints at exciting new phenomena such as the emergence of the Higgs boson in particle physics, or ferromagnetism in condensed matter physics.

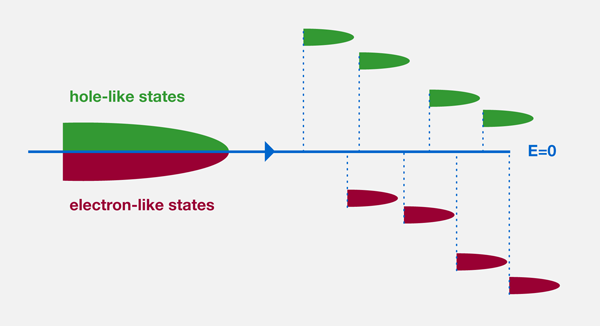
Very recently, two experimental groups—Yue Zhao, Paul Cadden-Zimansky, Zhigang Jiang, and Philip Kim at Columbia University in the US, reporting in the current issue of Physical Review Letters [1], and Harvard’s Benjamin Feldman, Jens Martin, and Amir Yacoby, also in the US [2]—have reported on the eightfold symmetry-breaking of the zero-energy Landau level in bilayer graphene systems (Fig. 1). The Columbia experiment used the typical setup of bilayer graphene on a ${SiO}_{2}$ substrate [3] and found that the unusual zero-energy quantum Hall octet, while intact at lower magnetic fields, splits up completely into eight separate Landau levels when exposed to $35 T$ (generated at the National High Magnetic Field Laboratory in Tallahassee, Florida, and close to the limit of what is currently possible for man-made static magnetic fields). The Harvard group used “suspended graphene,” an otherwise identical system, but where additional processing is used to remove the supporting ${SiO}_{2}$ substrate [4]. They report that the same symmetry breaking occurs at the more moderate magnetic field of about $3 T$ .

Before we can piece together what might be going on, we should first discuss what “bilayer graphene” is, and understand why one expects a quantum Hall octet state to occur at zero energy. Graphite is a well-known allotrope of carbon. Unlike diamond, its pricy cousin whose unit cell is an octahedron living in three spatial dimensions, graphite comprises a weakly coupled stack of two-dimensional carbon, with each layer being just one atom thick. The 2D carbon sheet is called graphene. In the plane, carbon naturally arranges itself into a honeycomb structure with single carbon atoms at the vertices, and strong $s p^{2}$ bonds along the edges.

In a strong magnetic field, the orbital motion of graphene electrons that are confined to a 2D plane becomes quantized into Landau levels and exhibits the quantum Hall effect [5]. Because the honeycomb is actually two identical, interpenetrating triangular lattices called $A$ and $B$ , the graphene Landau levels come in degenerate pairs with wave functions localized on the carbon atoms of either the $A$ or $B$ sublattice. This is known as “valley degeneracy” because in momentum space these wave functions are also localized around two distinct points (or valleys) in the hexagonal Brillouin zone. Further, since carbon is a light element, the electron spin and orbital motion in graphene are essentially decoupled, and different spin states are degenerate up to a small Zeeman splitting. Thus the spin and valley degrees of freedom give rise to the fourfold degeneracy of the monolayer graphene Landau levels in small fields.

Bilayer graphene is two electronically coupled graphene sheets. As a result one has two triangular lattices on the top layer and two on the bottom layer. The coupling between the layers is such that the atoms in one of the sublattices of the top layer interacts strongly with one of the sublattices in the bottom layer, pushing the corresponding energy bands out to higher energy. This leaves behind a low-energy system that is also described by two interpenetrating triangular lattices, except that one lattice is on the top layer and the other is on the bottom layer [6]. Therefore, in bilayer graphene, “layer degeneracy” is the same as “valley degeneracy.” However, quite unlike any other quantum Hall system, there is an additional degeneracy: the $n = 0$ and $n = 1$ Landau levels both have zero energy arising from the fact that the wave functions for both these states are localized in either the top or bottom layer. The zero-energy Landau level in bilayer graphene is therefore eightfold degenerate (spin, valley, Landau level) and is called a quantum Hall octet [3,6,7].

One could think of several mechanisms to break each of the individual degeneracies. For spin, just like for free electrons, a magnetic field distinguishes between spins that are parallel and antiparallel with the direction of the field. For layers, the top and bottom layers are not identical. For example, in suspended graphene, the bilayer sits over a trench etched out of the substrate, and a gate that lies below the substrate is used to change the carrier density. In this case, any applied gate voltage bends the layers into the trench (i.e., towards the gate) so that the curvature is always larger on the bottom layer. For nonsuspended graphene, the substrate itself obviously breaks the inversion symmetry. Finally, the weak hopping between carbon atoms that form the triangular lattice in the bottom layer and the atom in the top layer that lies in the center of a triangle breaks the Landau level degeneracy. But all of these mechanisms are expected to be very weak for noninteracting electrons and cannot by themselves explain the splitting of the quantum Hall octet.

The experiments [1,2] also suggest that the energy splitting of the eight new Landau levels is not directly related to any of these individual symmetry-breaking mechanisms, and that the splittings suddenly emerge at particular values of magnetic field, rather than a gradual transition. Moreover, just like in monolayer graphene, after a critical sample-dependent magnetic field, the new zero-energy quantum Hall plateau shows a diverging resistance as a function of both magnetic field and temperature [8]. All this hints that much richer physics is at play [6–10].

While it is fair to say that the nature of this symmetry breaking in bilayer graphene is still unknown, and indeed, other than the observation of the eightfold splitting, the two experiments themselves disagree in many important details [11], one could still speculate on its origin. Notably, suspended graphene is different in two important respects from graphene on a substrate. The substrate, being a dielectric material, effectively screens the Coulomb repulsion between electrons, implying that suspended graphene has much stronger many-body interactions. Secondly, the characteristic scale of disorder (charged impurities) in nonsuspended graphene is an order of magnitude larger since many of the trapped charges reside in the substrate.

One telling fact is that in both experiments, the emergent Landau level energy splittings are quite comparable to the energy scale that characterizes the disorder in the sample, estimated from zero-field transport studies [12]. The octet Landau level consists of both electronlike and holelike states, which would be broadened by this disorder energy scale (note the finite width of the levels shown in Fig. 1). In addition, disorder changes the local charge-neutrality point, breaking the sample up into a spatially inhomogeneous landscape of electronlike and holelike regions. One would then have local islands of quantum Hall metals (that are in different Landau level states) surrounded by insulating regions. Only when a percolating metallic path connects a single Landau level state from the source to the drain contacts would one then observe the transition from one quantum Hall plateau to another. The role of the (relatively large) Coulomb interaction between electrons in this inhomogeneous medium is an open problem and likely to be the key to understanding both the symmetry breaking of the zero-energy Landau level and the emergence of the highly resistive phase that was observed in both the monolayer and bilayer graphene experiments. As illustrated by these recent experiments, graphene research continues to deliver exciting new puzzles.

References

Y. Zhao, P. Cadden-Zimansky, Z. Jiang, and P. Kim, Phys. Rev. Lett. 104, 066801 (2010)
B. Feldman, J. Martin, and A. Yacoby, Nature Phys. 5, 889 (2009)
K. S. Novoselov et al., Nature Phys. 2, 177 (2006)
K. Bolotin et al., Solid State Commun. 146, 351 (2008); X. Du, I. Skachko, A. Barker, and E. Andrei, Nature Nanotech. 3, 491 (2008)
The Quantum Hall Effect, edited by R. Prange and S. Girvin (Springer-Verlag, New York, 1990)[Amazon][WorldCat]; Perspectives in Quantum Hall Effects, edited by S. Das Sarma and A. Pinzuk (John Wiley and Sons, New York, 1997)[Amazon][WorldCat]
E. McCann and V. Falko, Phys. Rev. Lett. 96, 086805 (2006)
Y. Barlas, R. Cote, K. Nomura, and A. MacDonald, Phys. Rev. Lett. 101, 097601 (2008)
J. Checkelsky, L. Li, and N. P. Ong, Phys. Rev. Lett. 100, 206801 (2008); Phys. Rev. B 79, 115434 (2009); S. Das Sarma and K. Yang, Solid State Commun. 149, 1502 (2009)
K. Yang, Solid State Commun. 143, 27 (2007)
D. A. Abanin, S. A. Parameswaran, and S. L. Sondhi, Phys. Rev. Lett. 103, 076802 (2009); R. Nankishore and L. Levitov, arXiv:0907.5395 (2009)
For example, the Columbia data show that the energy gaps scale as the square root of the magnetic field, while they scale linearly with field in the Harvard data
S. Adam and S. Das Sarma, Phys. Rev. B 77, 115436 (2008); S. Xiao et al., arXiv:0908.1329 (2009); S. Adam and M. D. Stiles, arXiv:0912.1606 (2009); S. Das Sarma et al., arXiv:0912.0403 (2009)

About the Author

Shaffique Adam is a NRC Postdoctoral Fellow at the Center for Nanoscale Science and Technology at the National Institute of Standards and Technology. He received a B.S. in physics from Stanford University, with departmental honors and a university distinction, and a Ph.D. in theoretical physics from Cornell University, where he studied the properties of nanoscale magnetic materials. Prior to joining NIST in 2009, Shaffique was a Postdoctoral Research Associate at the Condensed Matter Theory Center in the Department of Physics at the University of Maryland, College Park, investigating the transport properties of graphene.