First bounds on the Higgs boson from hadron colliders
In particle physics the interactions between particles are described by gauge symmetries that define the structure of the interactions and that are connected to exchange particles mediating the interaction. An elementary example familiar to everyone is the electromagnetic force mediated by photons. In the standard model of particle physics [1] this works beautifully, apart from the problem that all particles must be massless, which clearly contradicts experiment. This problem can be solved elegantly by the Higgs mechanism [2]. This mechanism gives mass to the particles by coupling them to a field that doesn’t vanish in the vacuum, but at the same time predicts the existence of a new particle, usually called the Higgs boson, which hasn’t been seen yet. Theory predicts all properties of this particle apart from its mass, which is a free parameter. In addition to giving mass to all particles, the Higgs is also responsible for keeping the interactions between massive gauge bosons—the W and Z bosons—at an acceptable level. To fulfill this second task the Higgs must be lighter than about 1TeV/c2.
To understand the mechanism of mass generation, we must either find the Higgs boson or exclude its existence (for a review, see Ref. [3]). The first searches for the Higgs were performed in the 1990s at LEP, an electron-positron collider at CERN near Geneva, Switzerland [4]. At LEP a Higgs boson would have been produced in association with a Z boson, which weighs around 90GeV/c2. With a center-of-mass energy of 205GeV, Higgs masses below 114.5GeV/c2 could be excluded. Further information about the Higgs mass comes from precision measurements. In quantum mechanics, the uncertainty principle allows that particles that are, in principle, too heavy to be produced can still exist for a very short time. At LEP and at the SLC in Stanford, the production of Z bosons has been studied with great precision. This makes the experiments sensitive to quantum effects coming from the Higgs. A similar sensitivity can be obtained from the precise measurements of the W mass, which has been done at LEP and at the Tevatron in Illinois. Taking all the precision measurements together in a global fit, it can be inferred that the Higgs must be lighter than around 200GeV/c2 [5].
At hadron colliders like the Tevatron, Higgs bosons are also produced at a significant rate [6]. A smaller fraction of them is produced in the same way as at LEP, by the annihilation of a quark-antiquark pair producing a Higgs together with a W or Z boson. The larger part of the Higgs boson production, however, comes from the annihilation of two gluons, the carriers of the strong force. In principle, the gluons are massless and thus should not couple to the Higgs. But even in this case, the uncertainty principle allows the production of intermediate particles that then couple to the Higgs. In the standard model these particles are usually top quarks, however, new, yet unknown particles can contribute as well.
The rate of Higgs boson production at the Tevatron is higher than at LEP. However, due to the huge backgrounds it is very difficult to find them. If the Higgs is lighter than about 130GeV/c2 it decays predominantly into a pair of bottom quarks. At higher masses, the decay into two W bosons takes over. The two experiments at the Tevatron, D0, and CDF have started to look for both decay modes. Since bottom-quark pairs are also produced by the strong interaction, the background in this channel is much larger, so that a longer running time is needed to find something. For this reason the experiments have now published first results in the WW channel in Physical Review Letters [7].
CDF and D0 search for both production channels, which means they either have two W bosons, two W bosons and one Z boson, or three W bosons in the final state. To get the background under control they require that two of the gauge bosons decay into a charged lepton and a neutrino, which is unseen, or two charged leptons in the case of a Z, so that the searched-for signature is two leptons and missing energy in the transverse plane.
There are still numerous backgrounds like W-pair production and top-quark-pair production, and to isolate a possible Higgs signal, sophisticated separation techniques must be used. Both experiments use neural networks trained at several Higgs masses. The neural networks are fed with many variables that carry some separation power between signal and background. With this procedure they manage to get a signal-to-background ratio of 1: 5 in the highest purity area if a Higgs with standard model properties exists. Great care is taken to model the backgrounds as accurately as possible, and when possible, data-Monte Carlo comparisons are used to constrain the background. The Higgs cross section is then fitted with a maximum likelihood technique, taking all systematic uncertainties into account.
The cross section turns out to be compatible with zero for all considered Higgs masses and the data are used to set a limit on the cross section, which is expressed as a scaling factor to the Higgs production cross section predicted by the standard model. A standard-model Higgs can then be excluded if a scaling factor of one is not compatible with the data. The results of the two experiments are then combined with statistical techniques that have been developed for the combination of the Higgs limits obtained by the four LEP experiments [8]. Although no experiment can individually exclude any Higgs mass, the combination of the two can exclude a region around MH=160GeV/c2. The limit is only strictly valid within the standard model. However, most extensions of the model predict a higher Higgs cross section, and the limit in those models would be even stronger.
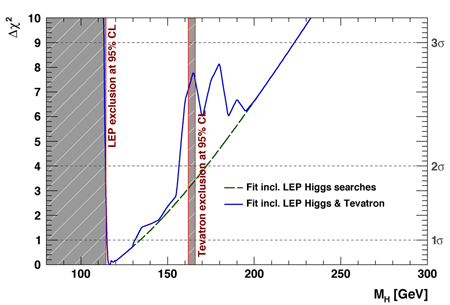
A global fit has been performed taking all information on the Higgs mass into account [9]. This comprises the electroweak precision data as well as the published Higgs limits from LEP and the Tevatron. Figure 1 shows the Δχ2 as a function of the Higgs mass with respect to the minimum χ2, with and without the Tevatron data. The low masses are excluded by LEP, the high masses by the precision data, and the region around 160GeV/c2 by the Tevatron. In the standard model, therefore, only the range between 115 and around 150GeV/c2 remains possible. For this region, preliminary analyses already exist at the Tevatron and it can be expected that D0 and CDF can exclude it or find a slight evidence if the Tevatron runs well for the rest of its lifetime. The LHC will then cover this region for sure. However, at the LHC energy range, it is experimentally even more difficult than at the Tevatron, so that we have to wait another couple of years. Moreover, if it turns out that there is physics beyond the standard model and the Higgs properties are not as predicted, the LHC should be able to say the final word about the existence of the Higgs. After 40 years of waiting, the search will end in the next decade.
References
- S. L. Glashow, Nucl. Phys. 22, 579 (1961); S. Weinberg, Phys. Rev. Lett. 19, 1264 (1967); A. Salam, in Elementary Particle Theory:Relativisitic Groups and Analyticity, Proceedings of the Eighth Nobel Symposium, Lerum, Sweden, 1968, edited by N. Svartholm (Almquist and Wiksells, Stockholm, 1968); M. Veltman, Nucl. Phys. B7, 637 (1968); B35, 167 (1971); G. ‘t Hooft and M. Veltman, B44, 189 (1972); B50, 318 (1972)
- P. W. Higgs, Phys. Lett. 12, 132 (1964); 13, 508 (1964); Phys. Rev., 145, 1156 (1966); F. Englert and R. Brout, Phys. Rev. Lett. 13, 321 (1964); G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble, 13, 585 (1964)
- G. G. Hanson, Physics 2, 106 (2009)
- ALEPH, DELPHI, L3, OPAL collaborations, and the LEP Working Group for Higgs Boson Searches, Phys. Lett. B 565, 61 (2003); arXiv:hep-ex/0306033
- ALEPH, DELPHI, L3, OPAL, SLD Collaborations, the LEP Electroweak Working Group, the SLD Electroweak, and Heavy Flavour Groups, Phys. Rep. 427 257 (2006); arXiv:hep-ex/0509008; ALEPH, DELPHI, CDF, D0, L3, OPAL, SLD Collaborations, the LEP Electroweak Working Group, the Tevatron Electroweak Working Group, the SLD Electroweak, and Heavy Flavour Groups, arXiv:0911.2604 (hep-ex)
- A. Djouadi, Phys. Rep. 457, 1 (2008); arXiv:hep-ph/0503172
- T. Aaltonen et al. (CDF Collaboration), Phys. Rev. Lett. 104, 061803 (2010); V. M. Abazov et al. (D0 Collaboration), 104, 061804 (2010)
- T. Aaltonen et al. (CDF and D0 Collaborations), Phys. Rev. Lett. 104, 061802 (2010)
- H. Flacher et al., Eur. Phys. J. C 60, 543 (2009); arXiv:0811.0009 (hep-ph)