Clean data with dirty surfaces in electrokinetics

Martin Z. Bazant

Viewpoint

Clean data with dirty surfaces in electrokinetics

Departments of Chemical Engineering and Mathematics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA

February 22, 2010• Physics 3, 18

Experiments now quantitatively confirm the standard model of electrokinetics, in which electric fields drive the flow of electrolytes, potentially leading to better sensors and biomedical diagnostic devices.

Figure caption — **Figure 1:** (a) The experimental setup, with a $50$ -micron-wide planar gold strip, coated with a silicon oxide film, on the floor of a elastomeric (polydimethylsiloxane-PDMS) microchannel, along which an alternating electric field is applied. (b) Simulation of the two rolls of induced-charge electro-osmotic flow generated above the gold strip, whose velocity along the surface is measured by image correlations observed with particle-image velocimetry (PIV). (Adapted from Ref. [6].)

Video 1: Fluid flow in an induced current electro-osmosis experiment with a

50

-micron-wide electrode covered with a

33 nm

silica coating. An ac electric field (

150 V/cm

,

500 Hz

) is applied horizontally in a solution of

10

micromolar

NaCl

. (Movie by A. Pascall and T. Squires, University of California, Santa Barbara.)

The field of electrokinetics, or electrically driven motion of particles and fluids, recently celebrated its $200$ th birthday [1,2] and yet it remains a frontier of theoretical physics. Stringent tests of the standard model used by workers in this field are now possible in microfluidic devices using alternating-current [3] or induced-charge electro-osmotic (ICEO) flows [4]. Unlike classical electro-osmosis, where the electric field acts on ions in the double layer screening a surface of fixed charge, ICEO flows involve electrically induced, rather than chemically derived, diffuse charge near polarizable (e.g., metal) surfaces, and this enables more direct tests of the theory. In most experiments, however, the model tends to under-predict observed velocities, sometimes by orders of magnitude [5]. Remarkably, the first quantitative agreement between theory and experiment, now reported in Physical Review Letters [6] by Andrew Pascall and Todd Squires at the University of California, Santa Barbara, involves the use of dirty metal surfaces, “controllably contaminated” by thin oxide films (Fig 1). Besides its fundamental significance, this work suggests that surface treatment may be the key to developing robust ICEO-based microfluidic devices.

Classical “fixed-charge” electrokinetic phenomena are linear in the applied voltage, since the electric field acts on pre-existing equilibrium double-layer charge to drive fluid flow. As such, Pascall and Squires describe the classical theory (developed by Helmholtz and Smoluchowski) as “interpretative” but not “predictive,” since the surface charge (or zeta potential) is a fitting parameter. In contrast, ICEO flows result from electrostatically induced charge, set by the applied voltage, and in the standard model for an ideally polarizable surface (at constant potential without passing current), there are no adjustable parameters, except for a parasitic surface capacitance, to represent a solvation (Stern) layer or dielectric coating. This model has predicted many new phenomena, such as flows around metallic particles [7], mixing by metallic posts [8], transverse electrophoresis of metal/dielectric Janus particles [9], and pumping by microelectrode arrays [10], but it lacks quantitative accuracy and fails to predict some features, such as flow reversal and solution dependence [5].

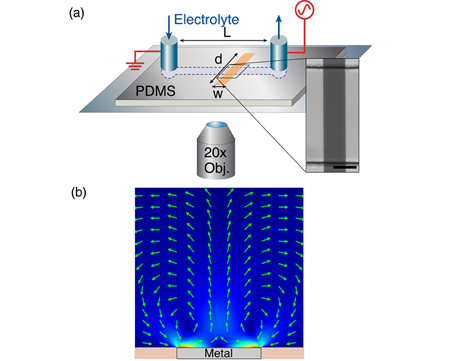
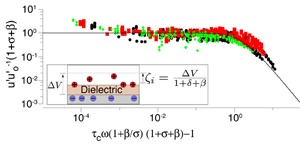
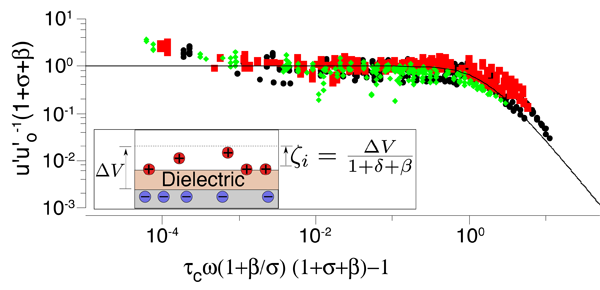
Pascall and Squires developed a new experimental platform to study ICEO flows with unprecedented control [Fig. 1, panel (a)]. Their setup is similar to that of Levitan et al. [11], who reconstructed the ICEO flow around a platinum cylinder by particle-image velocimetry, but with two crucial innovations: (i) They used a flat gold stripe on the floor of the channel, which has a much simpler, linear velocity profile in the microscope focal plane [Fig. 1, panel (b), and Video 1], and (ii) they coated the metal with evaporated silica films of precisely controlled thickness. The latter resulted in a known film capacitance in series with the double-layer capacitance, which allowed reasonable prediction of $987$ different conditions of film thickness, voltage, frequency, and (dilute) $NaCl$ or $KCl$ concentration. An even better collapse of the data (Fig. 2) resulted from also fitting a parallel “buffer capacitance,” representing the dissociation of protons from silanol groups on the silica surface.

The collapse of such a wide range of data with only two parameters, each of which can be estimated separately, convincingly establishes the validity of the standard model, at least for small diffuse-layer voltages. These results also show that more attention must be paid to electrochemical boundary conditions. The buffer capacitance is usually neglected, and a recent theoretical study has also demonstrated the importance of accounting for the surface adsorption of ions [12].

For both fundamental and practical reasons, the next steps should be to reduce the film thickness and explore other interfacial chemistries, which enable faster flows, by reducing the voltage drop across the surface coating. The observed flows are hundreds of times slower than the state of the art in ac electro-osmotic pumping by bare gold microelectrodes [13]. Such devices transmit much larger voltages ( $100$ times the thermal voltage, $25$ $mV$ ) to the double layer, which may lead to ion crowding and other electrochemical processes, not described by the standard model [5]. These effects may be responsible for the practical limitation of ICEO flows to dilute solutions ( $< 10 mM$ of simple salts in water), which does not seem to be overcome by the silica coating. Arguably, the ”holy grail” would be a surface treatment that allows robust, fast ICEO flows in $1 M$ physiological solutions, since this could enable portable or implantable biomedical lab-on-a-chip devices. What the field needs now is equally clean data for less dirty surfaces.

References

F. F. Reuss, Memoires de la Societe Imperiale des Naturalistes de Moscou 2, 327 (1809)
J. Lyklema, Colloids Surf. A 222, 5 (2003)
A. Ramos, H. Morgan, N. G. Green, and A. Castellanos, J. Colloid Interface Sci. 217, 420 (1999)
M. Z. Bazant and T. M. Squires, Phys. Rev. Lett. 92, 066101 (2004)
M. Z. Bazant, M. S. Kilic, B. Storey, and A. Ajdari, Adv. Colloid Interface Sci. 152, 48 (2009)
A. J. Pascall and T. M. Squires, Phys. Rev. Lett. 104, 088301 (2010)
V. A. Murtsovkin, Colloid J. 58, 341 (1996)
C. K. Harnett, J. Templeton, K. A. Dunphy-Guzman, Y. M. Senousya, and M. P. Kanou, Lab Chip 8, 565 (2008)
S. Gangwal, O. J. Cayre, M. Z. Bazant, and O. D. Velev, Phys. Rev. Lett. 100, 058302 (2008)
V. Studer, A. Pépin, Y. Chen, and A. Ajdari, Analyst 129, 944 (2004)
J. A. Levitan, S. Devasenathipathy, V. Studer, Y. Ben, T. Thorsen, T. M. Squires, and M. Z. Bazant, Colloids Surf. A 267, 122 (2005)
Y. K. Suh and S. Kang, Phys. Rev. E 79, 046309 (2009)
C. C. Huang, M. Z. Bazant, and T. Thorsen, Lab Chip 10, 80 (2010)

About the Author

Martin Z. Bazant is an Associate Professor of Chemical Engineering and Applied Mathematics at the Massachusetts Institute of Technology. After completing a Ph.D. in condensed matter physics at Harvard University in 1997, he joined the MIT faculty in applied mathematics in 1998 and in chemical engineering in 2008. He has held the Paris Sciences Chair and Joliot Chair at Ecole Supérieure de Physique et Chimie Industrielles, he received an Early Career Award from the Department of Energy in 2002, and was among the “Brilliant Ten” scientists selected by Popular Science Magazine in 2007. His research focuses on electrokinetics, microfluidics, and electrochemical systems.