Taking the temperature of extreme matter

Charles Gale

Viewpoint

Taking the temperature of extreme matter

Department of Physics, McGill University, Montréal, QC H3A 2T8, Canada

March 29, 2010• Physics 3, 28

Researchers at the Relativistic Heavy Ion Collider have now measured the temperature of hot dense matter created in a nuclear collision.

Figure caption — **Figure 1:** The QCD phase diagram with a possible critical line: A first-order phase transition terminating at a critical endpoint. The temperature region deduced by the PHENIX collaboration appears in blue.

The study of hot dense matter defines a vast area of science that currently generates and enjoys tremendous theoretical and experimental activity in many fields. This palette of scientific enquiries comprises several disciplines in physics; condensed matter physics and plasma physics are good examples. Moving up in energy, we find nuclear and particle physics, astrophysics, and cosmology. At the top end of this scale, the physics of matter under extreme conditions of temperature and density involves the theory of the strong interaction—quantum chromodynamics (QCD)—and seeks to answer questions like the following [1]: What happens deep in the interior of a neutron star? What is the phase diagram of matter governed by QCD? As reported in Physical Review Letters [2] and Physical Review C [3], researchers at Brookhaven National Laboratory have now brought us closer to this goal by measuring a fundamental property—the temperature of extremely hot matter.

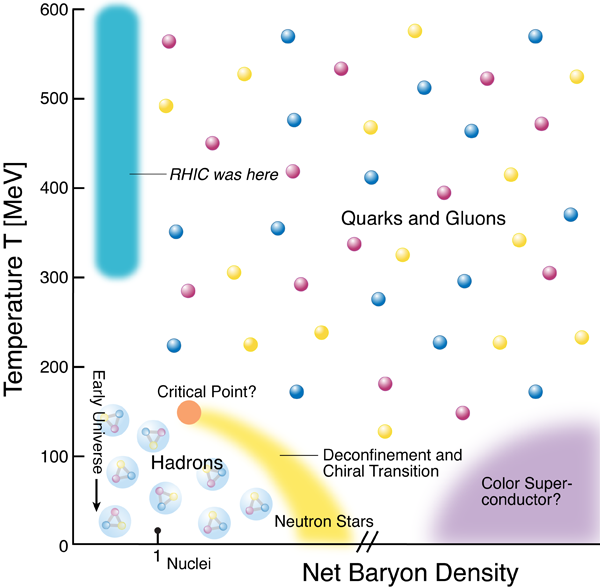
The Relativistic Heavy Ion Collider (RHIC), now finishing its first decade of operation at Brookhaven National Laboratory, is an accelerator complex devoted to studying the many facets of QCD. It has a research program that aims to quantitatively understand the individual contributions of the proton’s building blocks (quarks and gluons) to its spin, and a heavy-ion program. In the latter, large gold nuclei are accelerated to a speed very close to that of light, and collided to create a volume of hot and dense hadronic matter, larger and more energetic than the nucleons making up atomic nuclei. One of the goals of RHIC is to study the bulk, many-body, behavior of QCD and to elucidate its phase diagram (Fig. 1). In this context, numerical implementations of QCD on a spacetime lattice have predicted a transition from the physical phenomena associated with “ordinary” hadronic matter (nucleons, pions, etc.) to those of the constituent quarks, antiquarks, and gluons. It is also expected that this change should happen when the temperature approaches and exceeds $T_{c} \sim 170 MeV$ (recall that $1 MeV \approx 10^{10} K$ ).

In its goal of forming and characterizing this new and unusual form of matter, often called a “quark-gluon plasma,” RHIC has discovered a wealth of new phenomena that unambiguously signal exciting new physics. For example, the transverse momentum spectra of measured “soft” (low-energy) particles emitted from the nuclear collisions at RHIC, together with their azimuthal anisotropy, are remarkably consistent with simulations relying on ideal relativistic hydrodynamics (i.e., where the viscosity is essentially zero) [4]. For higher values of transverse momenta, the original expectations that the dynamics would be compatible with predictions of perturbative QCD (pQCD) were shown to be incorrect. At energy values similar to those accessed by RHIC, the perturbative version of quantum chromodynamics (pQCD) is found to work well in studies of nucleon-nucleon collisions. Defining an experimental variable for measured hadrons that is unity if nuclear collisions are simply a superposition of proton-proton collisions, $R_{AA} = (d N_{AA} / d p_{T}) / [N_{coll} (d N_{pp} / d p_{T}$ )] (where $N_{coll}$ is the number of binary collisions), RHIC has shown very convincingly that $R_{AA}$ remains low up to high values of transverse momentum $p_{T}$ . This very strongly suggests that energetic QCD jets are quenched by the strongly interacting medium and that they fragment into the measured hadrons with less energy [5]. These and other compelling discoveries made by RHIC have brought initial hopes and expectations into a sharper focus: Some early estimates predicted the QGP would behave as a weakly interacting gas. It now appears instead to be strongly coupled—an “sQGP”—that is, it is more like a “liquid” than a gas.

RHIC is now moving into an exciting characterization phase, and will further quantify the properties of the sQGP. In this task, the use of penetrating probes is an invaluable asset. Electromagnetic radiation plays a special role here: since the mean free path of photons is much larger than typical nuclear scales, the photons will leave the interaction zone unscathed and fly off to the detectors. This advantage, however, also has its drawbacks: The smallness of the electromagnetic coupling constant, $α_{EM} = 1 / 137$ , which sets the size of the signal, complicates the task of extracting information. In addition, photons (real and virtual) are emitted throughout the history of the nuclear interaction and theoretical modeling of the entire spacetime evolution is therefore necessary to interpret the measurements.

The PHENIX collaboration has carried out a measurement of the “direct” photons emitted in relativistic nuclear collisions of gold nuclei at RHIC, at a collision energy of ${\sqrt{s}}_{NN} = 200 GeV$ [2]. The direct photons are those not associated with the decay of hadronic particles; they are thus good clean probes of the thermal, strongly interacting medium. PHENIX observes a large excess of direct photons in Au-Au collisions over what is expected from appropriately scaled $p$ - $p$ results. This measurement represents a breakthrough on several fronts. First, it exploits a clever experimental technique that consists of extrapolating the results of virtual photon measurements (involving pairs of opposite charge leptons) to zero lepton pair invariant mass [6], and interpreting them as measurements of real photons [3]. This technique has been verified for consistency in proton-proton collisions. Second, by fitting the nucleus-nucleus photons to a thermal source, the PHENIX collaboration is able to get a temperature.

This temperature is an “effective temperature,” owing to at least two reasons: (1) Photons are emitted throughout the collision process, as the temperature evolves. Different phases at different values of temperature will then contribute to what is measured at low $p_{T}$ . (2) The hydrodynamic medium develops an outward flow [7], which can affect transverse momentum spectra and will therefore cause apparent temperatures to shift upwards. For central $Au-Au$ collisions (almost head-on), the PHENIX collaboration deduces an effective temperature of $T = 221 \pm 19$ (statistical) $\pm 19$ (systematic) $MeV$ . The “true” initial temperature, $T_{init}$ , is then obtained by relying on theoretical models. As those may differ in detail, this PHENIX result carries an uncertainty that can be attributed to theory. Models with $300 MeV \leq T_{init} \leq 600 MeV$ are in apparent agreement with the PHENIX data [2,3]. Note that even the lower bound largely exceeds the $T_{c}$ value deduced from lattice QCD.

It is fair to write that this temperature determination represents a definite milestone, if confirmed, in the quantification of the sQGP and in the determination of its precise properties. It also constitutes an invitation to theorists to further refine their own simulations, which will be applied to other exciting results still to come from RHIC and from the heavy-ion program beginning at the LHC. RHIC is now making progress in precise quantitative measurements of some of the most basic physical quantities needed to understand matter at the top of the temperature scale.

References

Joseph I. Kapusta and Charles Gale, Finite-Temperature Field Theory: Principles and Applications (Cambridge University Press, Cambridge, 2006)[Amazon][WorldCat]
A. Adare et al. (PHENIX Collaboration), Phys. Rev. Lett. 104, 132301 (2010)
A. Adare et al. (PHENIX Collaboration), Phys. Rev. C 81, 034911 (2010)
M. Gyulassy and L. McLerran, Nucl. Phys. A 750, 30 (2005)
K. Adcox et al., Phys. Rev. Lett. 88, 022301 (2002)
The invariant mass M is defined as M = √(E² - p²), where E and p are the total energy and momentum of the set of particles being considered. If the set contains only one particle, it is the rest mass
S. A. Voloshin, A. M. Poskanzer, and R. Snellings, arXiv:0809.2949 (nucl-ex)

About the Author

Charles Gale is James McGill Professor and Chair of the Department of Physics at McGill University. His research straddles nuclear and particle physics and concentrates mainly on the physics of hot and dense strong interacting matter. He has been elected Fellow of the American Physical Society, and Fellow of the American Association for the Advancement of Science.