Combing a qubit

Boris Blinov

Viewpoint

Combing a qubit

Boris Blinov

Department of Physics, University of Washington, Seattle, WA 98195, USA

April 5, 2010• Physics 3, 30

A trick for modulating optical frequency combs will enable more flexible control over trapped-ion qubits.

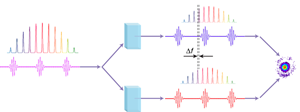
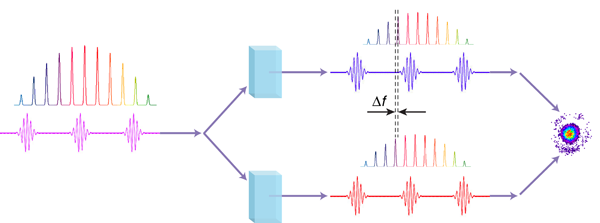
Figure caption — **Figure 1:** The spectrum of pulse trains from a mode-locked laser consists of a sequence of optical frequencies that are evenly spaced–an optical frequency comb. Pairs of frequencies formed from two “teeth” on the comb have a definite phase relationship with one another and the pair can control a spin qubit on a trapped ion via a stimulated Raman process. Hayes *et al.* extend this capability to any frequency by splitting the pulses and shifting each with an acousto-optic modulator.

Heralded as “millions of ultra-stable lasers in one,” ultrafast optical frequency combs [1] —the subject of the 2005 Nobel Prize in Physics—have become a ubiquitous tool in precision metrology labs. In simple terms, a frequency comb (Fig. 1) is the spectrum of equally spaced optical frequencies produced by the train of short laser pulses that emerge from a mode-locked laser. The distance between pulses determines the comb’s frequency spacing, while the length of the individual pulse sets the overall bandwidth of the comb (the shorter the pulse, the greater the bandwidth). In a new twist to the many applications of optical frequency combs, the possibility of using them to control the spin state of ion qubits is becoming highly attractive in the field of quantum information processing. Writing in Physical Review Letters, David Hayes and colleagues at the Joint Quantum Institute at the University of Maryland in the US, demonstrate a technique that gives optical frequency combs the flexibility to rotate and entangle ion-spin qubits over a wide frequency range [2].

The most essential ingredient for quantum information processing, be it based on atoms, molecules, quantum dots, or superconducting circuits, is, arguably, the ability to precisely control the quantum states of the qubits. The stable, narrow-band emission from continuous-wave lasers has been the master of this task in the study of trapped ion qubits for many years [3,4]. Consider, for example, a trapped ion qubit spanned by the hyperfine levels of the ion’s ground state. To control its spin state, one uses a stimulated Raman setup, where two phase-locked laser beams, whose frequencies differ by exactly the frequency splitting of the two spin states on the qubit, can both cause the bit to flip its spin and perform entangling operations. (The reason for using lasers, instead of microwaves that directly link the qubit states, is because they impart the necessary momentum kick to flip the ion’s spin.) To minimize spontaneous emission, the laser Raman frequencies are typically very far detuned from any optical transition in the qubit atom.

The key point is that the two laser beams must be phase locked in order to drive a coherent transition between the qubit states. There are two ways to do this: either modulate a single continuous-wave laser beam at the appropriate frequency, or lock two separate lasers to a common source. These systems work wonderfully, and produce beautiful results, but the effort that goes into generating a laser beam that can drive the Raman transition is not insignificant. Since the lasers are detuned from the atomic optical transitions and the rate of bit flips is inversely proportional to the detuning, they have to be very powerful to set the qubit states at a reasonable speed. In addition, to generate laser beams that effectively excite a typical trapped ion qubit, whose transitions lie in the ultraviolet spectrum, often involves shifting the laser’s frequency with nonlinear optical processes, such as second harmonic generation. The efficiency of such processes is quite low for continuous-wave light, so achieving these high power levels is challenging. Another problem arises if the frequency splitting between states on the qubit is large. In these cases, conventional techniques for modulating the laser beam are difficult or inefficient. For example, in the first demonstration of stimulated Raman control of a cadmium ion, where the qubit states were formed by a hyperfine splitting of approximately $14.5 GHz$ , it was necessary to use a high-frequency electro-optic modulator (EOM) in conjunction with a Mach-Zehnder interferometer [5]. Even then, in the best case scenario, only about $25 %$ of the laser beam power was available to drive the transition, the rest interfered destructively and gave rise to unwanted ac Stark shifts in the atoms.

Frequency combs provide a powerful alternative to these conventional techniques for producing two lasers with a set, phase-locked separation in frequency. A typical mode-locked laser produces a train of fast pulses formed by interference of thousands, or even millions, of longitudinal modes of the laser cavity and the typical pulse repetition rate is about $100 MHz$ . This sets the separation between the allowed frequencies—or “teeth”—in the frequency comb to 100 MHz. The spectrum of a picosecond pulse train contains over $10, 000$ comb teeth. To drive a stimulated Raman transition at, for example, $10 GHz$ , every comb “tooth” will work together with its 100th counterpart (exactly $100 \times 100 MHz = 10 GHz$ away) to form the effective Raman beam pair. The teeth from the frequency comb all come from the same laser cavity and are thus automatically phase-coherent with each other. In effect, one gets thousands of Raman lasers in a single beam.

But what if the qubit transition of interest is not at $10 GHz$ , or any integer number of comb intervals? Then one may, for example, change the laser repetition rate by carefully adjusting the length of the laser cavity so that the integer number of comb teeth would span the relevant transition frequency. The University of Maryland group presents another, more elegant way (Fig. 1 ). They split the ultrafast laser beam in two and each beam is then sent through an acousto-optic modulator (AOM). These modulators effectively add or subtract the same fixed frequency to each frequency in the comb, and since the two AOMs run at different frequencies, individual teeth from one beam form Raman pairs with the teeth in the other beam. Given a $100 MHz$ comb spacing, it is sufficient to detune the two AOMs by up to $50 MHz$ to hit any possible transition within the comb bandwidth.

The use of mode-locked lasers has advantages. The high instantaneous power of the short laser pulses makes all nonlinear optical processes very efficient. It is possible, for example, to produce Raman beams at visible and ultraviolet wavelengths with single-pass second-harmonic generation in nonlinear crystals. At the same time, the high intensity of the Raman beams may lead to large and potentially destructive (from the qubit coherence point of view) ac Stark shifts. With the University of Maryland group’s flexible frequency comb, this problem can be reduced and even eliminated by tuning the Raman beams to the “magic” wavelength in between the two fine structure lines in the first excited $P$ state. At that wavelength, the ac Stark shifts due to the lower and the upper fine structure level exactly cancel each other, while the Raman transition amplitudes add constructively. While Hayes and colleagues did not use this magic wavelength in their present work, the next step in their research project is to use a picosecond third-harmonic $Nd$ :YAG laser at $355 nm$ , which is almost exactly at the magic wavelength of the ytterbium ion they are studying now.

The broad bandwidth of mode-locked lasers ( $THz$ or more) makes this technique applicable to many systems, such as molecules, Rydberg atoms, and quantum dots. Coherent control with these frequency combs can be very fast, requiring only a few pulses per gate. In an extreme case of ultrafast laser control of trapped ion qubits, a single pulse can coherently transfer the population, and a few pulses can generate entanglement and quantum gates between ions [6,7]. Obviously, the physics of single-pulse coherent control is somewhat different since no comb is present in the frequency domain with just one pulse. However, the basic idea of controlling cold atoms and ions with ultrafast laser pulses remains, and the broader application of this idea seems natural. The University of Maryland group has made important contributions in developing these techniques to demonstrate laser cooling of trapped atoms with broadband pulses [8], and to impart a controlled phase shift on a trapped ion qubit [9]. More exciting physics is sure to come from the intersection of cold atoms and broadband pulses in the near future.

References

Femtosecond Optical Frequency Comb Technology: Principle, Operation, and Applications, edited by J. Ye and S. T. Cundiff (Springer, New York, 2005)[Amazon][WorldCat]
D. Hayes, D. N. Matsukevich, P. Maunz, D. Hucul, Q. Quraishi, S. Olmschenk, W. Campbell, J. Mizrahi, C. Senko, and C. Monroe, Phys. Rev. Lett. 104, 140501 (2010)
C. Monroe, D. Meekhof, B. King, W. Itano, and D. Wineland, Phys. Rev. Lett. 75, 4714 (1995)
H. C. Nägerl, Ch. Roos, D. Leibfried, H. Rohde, G. Thalhammer, J. Eschner, F. Schmidt-Kaler, and R. Blatt, Phys. Rev. A 61, 023405 (2000)
P. J. Lee, B. B. Blinov, K. Brickman, L. Deslauriers, M. J. Madsen, R. Miller, D. L. Moehring, D. Stick, and C. Monroe, Opt. Lett. 28, 1582 (2003)
J. J. García-Ripoll, P. Zoller, and J. I. Cirac, Phys. Rev. Lett. 91, 157901 (2003)
L.-M. Duan, Phys. Rev. Lett. 93, 100502 (2004)
B. B. Blinov, R. N. Kohn, Jr., M. J. Madsen, P. Maunz, D. L. Moehring, and C. Monroe, J. Opt. Soc. Am. B 23, 1170 (2006)
M. J. Madsen, D. L. Moehring, P. Maunz, R. N. Kohn, Jr., L.-M. Duan, and C. Monroe, Phys. Rev. Lett. 97, 040505 (2006)

About the Author

Boris Blinov graduated from Moscow State University in 1995 and received his Ph.D. from the University of Michigan in 2000, working on polarized beam storage and acceleration. In 2001 he joined Christopher Monroe’s group at the University of Michigan as a postdoctoral fellow, where he explored trapped-ion quantum computing. In September of 2005 he became an Assistant Professor of Physics at the University of Washington. (Photo by Aleksey Blinov.)