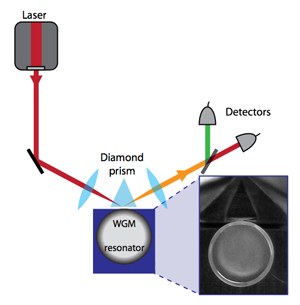
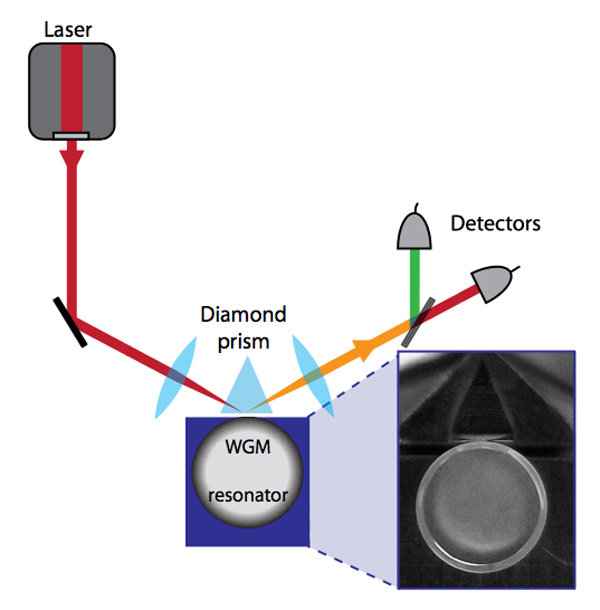
Second-harmonic generation in microresonators through natural phase matching

Tobias J. Kippenberg

Viewpoint

Second-harmonic generation in microresonators through natural phase matching

Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland

April 12, 2010• Physics 3, 32

Researchers have found a way to naturally double the frequency of laser light with an optical microresonator made from lithium niobate that supports “whispering gallery” modes.

Figure caption — **Figure 1:** Schematic of the experiment performed by Fürst *et al.* The inset shows the resonator. (Adapted from Ref. [2].)

Resonators are ubiquitous in physics, and recently much effort has gone into developing optical microresonators that offer strong spatial and long temporal confinement. The basic principle relies on the fact that light can be trapped inside a microresonator via continuous total internal reflection. The modes formed in this manner are also known as “whispering gallery modes” (WGM), since they are an optical analogy to the acoustical effect that was observed by Lord Rayleigh in Saint Paul’s cathedral in which sounds travel efficiently along a curved wall [1]. Now, in a paper published in Physical Review Letters, Josef Fürst, Dmitry Strekalov, Dominique Elser, Mikael Lassen, Ulrik Andersen, Christoph Marquardt, and Gerd Leuchs from the Max Planck Institute for the Science of Light (Erlangen), the University of Erlangen-Nuremberg, both in Germany, the Jet Propulsion Laboratory in Pasadena, US, and the Technical University of Denmark report a way to easily generate the second harmonic of laser light using such resonators [2] (see Fig. 1).

Optical WGM resonators have a natural “figure of merit”: their optical quality factor $Q$ , which expresses their ability to confine light for long amounts of time. While it has long been known that dielectric particles exhibit whispering gallery mode resonances, it was the observation of ultrahigh $Q$ modes that led to optical microresonators being widely employed [3]. Ultrahigh $Q$ modes at optical wavelengths were first demonstrated in 1989 by Braginsky and Gorodetsky [4] in silica microspheres, and remarkably high $Q$ values exceeding ten billion ( $10^{9}$ ) have been observed. In the last decade, several other varieties of ultrahigh $Q$ microresonators have emerged, which lead to a wide range of new microresonator applications in cavity quantum electrodynamics [5,6], nonlinear optics [7,8], cavity optomechanical studies [9], or cavity enhanced sensing schemes. On-chip silica microtoroids have been discovered [10] that allowed bringing this $Q$ factor into a chip scale. While microtoroids and microspheres employ fused silica as the material of the dielectric, a versatile method to extend ultrahigh $Q$ to other materials has been developed by the Jet Propulsion Laboratory in Pasadena, US. By simply polishing a cylinder blank [11] (such as pure ${CaF}_{2}$ crystals), $Q$ factors exceeding ten billion have been demonstrated, only limited by residual surface roughness.

In contrast to fused silica, crystalline materials have the distinct advantage of being extraordinarily transparent to frequencies from ultraviolet to the mid-infrared. In addition, these materials exhibit low mechanical dissipation [12], which make them appealing for optomechanical studies. The highest optical finesse (the power enhancement factor) demonstrated to date is $10^{7}$ [13], which implies that only $1 μ W$ of power gives rise to $10 W$ of circulating power inside the crystalline microresonator. Not surprisingly, at such power levels (and due to the small transverse confinement high intensity), a rich set of nonlinear phenomena have been observed in microresonators, for instance, Raman lasing [7], Brillouin scattering [14], parametric oscillations [15,16] and optical frequency comb generation [17,18]. A common feature of these nonlinear oscillations in microresonators is their exceptionally low threshold; threshold levels for nonlinear oscillation are regularly in the sub- $μ W$ regime, values that are traditionally associated with linear optics. In addition, radiation pressure interactions have been observed in both silica microresonators [19,20] as well as crystalline resonators [21], whereby the mechanical modes of the microresonators interact with the optical modes. So far, however, most of the nonlinear optical studies have relied on silica or crystalline resonators made out of materials that lack inversion symmetry and therefore only contain a third-order nonlinearity.

A natural extension has been the development of resonators with a second-order nonlinearity, a necessity for processes such as frequency doubling of laser light. Second-order nonlinear materials are particularly interesting from the perspective of quantum optics. The second-order process annihilates two pump photons and creates a photon with twice the frequency and hence twice the energy, which can give rise to optical squeezing [22]. A natural step would hence be to combine the ultralow-loss optical microresonators with a second-order nonlinearity to achieve second-harmonic generation. The paper by Fürst et al.—following pioneering work at the Jet Propulsion Laboratory [11]—the work makes a further important step in this direction. The challenge of making a resonator out of a second-order nonlinear material was relaxed with the advent of micropolishing techniques—by polishing a circular blank (with mm-scale size) of ${LiNbO}_{3}$ , high $Q$ resonators have been fabricated whose quality factor ( $Q$ of the order of $10^{7}$ ) is only limited by the material quality [23]. In order to generate a second-harmonic field, however, phase matching has to be obeyed.

For phases to be matched, the wave vectors for the two frequencies have to obey the law of conservation of momentum. The WGM resemble mathematically the solutions for the orbitals of a hydrogen atom, characterized by an azimuthal, angular, and radial mode number (as well as a polarization). Just as in the case of atomic transitions, selection rules apply to, and govern, the second-order nonlinear interaction. As the optical modes are angular momentum eigenstates, the second-order nonlinear interaction requires conservation of the angular momentum mode number. Hence for a given pump frequency, this fixes the angular mode number of the mode in which the second harmonic is converted. This condition means that the second-harmonic generation mode must carry twice as much angular momentum as the pump mode, implying that the mode number of the scattered mode is $2 l$ , when the pump mode has angular momentum $l$ . This condition can always be satisfied. However, the frequency of the second harmonic needs to also satisfy energy conservation—if the resonator is pumped at frequency $ω$ , the optical mode with twice the angular momentum ( $2 l$ ) must exist precisely at frequency $2 ω$ in order for second-harmonic generation to be able to take place. Due to the small size of the resonators and the high $Q$ , the latter is enormously challenging. In the past, phase matching in microresonators had been achieved using periodic poling of the ${LiNbO}_{3}$ , however, the method relied on accidental frequency matching [23].

The Letter by Fürst et al. takes a much more practical and reliable route to achieve phase matching. Using the fact that the crystal has two refractive indices associated with the ordinary and extraordinary direction of propagation, which, importantly, exhibit different temperature dependence, one can achieve a differential tuning of the pump mode with respect to the second harmonic. This thereby allows continuous tuning of the relative frequency between the pump and the second harmonic until the two satisfy the law of conservation of energy. In this manner, the authors observe efficient second-harmonic generation. This method therefore opens up to study these phenomena in a reliable manner.

The implications of this work are manifold. First, the resonators can serve as efficient doubling cavities, in particular when combined with efficient tapered optical fiber coupling. More fascinating, however, is the ability to generate squeezed states of light. Squeezing of the pump laser as well as the generated second-harmonic generation should be possible, which makes compact sources of squeezed light a tantalizing possibility. While it is yet not clear if other obstacles such as thermorefractive noise [24] may impede such studies, certainly one aspect is clear: the quest for ultrahigh $Q$ in microresonators continues to bring new advances in a wide range of fields, making them even more indispensible in the future.

References

L. Rayleigh, Scientific Papers (Cambridge University Press, Cambridge, 1912)
J. U. Fürst, D. V. Strekalov, D. Elser, M. Lassen, U. L. Andersen, C. Marquardt, and G. Leuchs, Phys. Rev. Lett. 104, 153901 (2010)
K. J. Vahala, Nature 424, 839 (2003)
V. B. Braginsky, M. L. Gorodetsky, and V. S. Ilchenko, Phys. Lett. A 137, 393 (1989)
T. Aoki et al., Nature 443, 671 (2006)
D. W. Vernooy et al., Phys. Rev. A 57, R2293 (1998)
S. M. Spillane, T. J. Kippenberg, and K. J. Vahala, Nature 415, 621 (2002)
A. A. Savchenkov et al., Phys. Rev. Lett. 93, 243905 (2004)
T. J. Kippenberg and K. J. Vahala, Opt. Express 15, 17172 (2007)
D. K. Armani et al., Nature 421, 925 (2003)
V. S. Ilchenko et al., Phys. Rev. Lett. 92, 043904 (2004)
V. B. Braginsky, V. P. Mitrofanov, and V. I. Panov, Systems with Small Dissipation (University of Chicago Press, Chicago, 1985)[Amazon][WorldCat]
A. A. Savchenkov et al., Opt. Express 15, 6768 (2007)
I. S. Grudinin, A. B. Matsko, and L. Maleki, Phys. Rev. Lett. 102, 043902 (2009)
A. A. Savchenkov, A. B. Matsko, D. Strekalov, M. Mohageg, V. S. Ilchenko, and L. Maleki, Phys. Rev. Lett. 93, 243905 (2004)
T. J. Kippenberg, S. M. Spillane, and K. J. Vahala, Phys. Rev. Lett. 93, 083904 (2004)
P. Del’Haye et al., Nature 450, 1214 (2007)
A. A. Savchenkov et al., Phys. Rev. Lett. 101, 093902 (2008)
T. J. Kippenberg and K. J. Vahala, Science 321, 1172 (2008)
Florian Marquardt and Steve Girvin, Physics 2, 40 (2009)
J. Hofer, A. Schliesser, and T. J. Kippenberg, arXiv:0911.1178v2
S. F. Pereira, Min Xiao, H. J. Kimble, and J. L. Hall, Phys. Rev. A 38, 4931 (1988)
V. S. Ilchenko et al., Phys. Rev. Lett. 92, 043903 (2004)
M. L. Gorodetsky and I. S. Grudinin, J. Opt. Soc. Am. B, 21, 697 (2004)

About the Author

Tobias J. Kippenberg is Associate Professor of Physics and Electrical Engineering at EPFL and leads the Laboratory of Photonics and Quantum Measurement. He obtained his B.A. at the RWTH Aachen, and M.A. and Ph.D. at the California Institute of Technology (Caltech in Pasadena, US). From 2005 to 2009 he led an Independent Research Group at the MPI of Quantum Optics. He is an alumnus of the Studienstiftung des Deutschen Volkes and winner of the 8th EU Contest for Young Scientists (1996) for his invention of an infrared-microwave radiation ice condition sensor for cars. For his invention of chip-scale frequency combs, he is co-recipient of the Helmholtz Price for Metrology (2009). Moreover, he is recipient of the EFTF Young Investigator Award (2010) and the EPS Fresnel Prize (2009).