Controlling the martensitic transition in Heusler shape-memory materials

Antoni Planes

Viewpoint

Controlling the martensitic transition in Heusler shape-memory materials

Departament d'Estructura i Constituents de la Matèria, Facultat de Física, Universitat de Barcelona, Diagonal 647, Barcelona, E-08028 Catalonia, Spain

April 26, 2010• Physics 3, 36

Understanding the electronic structure of shape-memory alloys promises magnetic control over their crystal structures and hence mechanical properties.

Figure caption — **Figure 1:** Crystal structures and phase diagram of $Ni-Mn-Sn$ . The shadowed area in the phase diagram is the region where $Ni-Mn-Sn$ , on cooling, first becomes ferromagnetic and later transforms martensitically. (A) The $L 2_{1}$ structure showing also the relationship with the tetragonal unit cell. (B) Tetragonal ( $L 1_{0}$ ) unit cell. (C) The tetragonal unit cell viewed from top. (D) The martensitic structure constructed from nanotwinned variants of the $L 1_{0}$ structure.

Magnetic shape-memory properties occur in magnetic materials undergoing a martensitic transition, which is a transition from a cubic atomic structure to a layered structure that is dominated by strain. These materials show a strong change of shape in response to an applied magnetic field. The shape change is caused either by inducing a structural martensitic transition, or by rearranging twin related domains in the martensitic state. In 1996, O’Handley and collaborators at MIT first suggested the possibility of magnetic control over the shape-memory effect in a ferromagnetic ${Ni}_{2} MnGa$ “Heusler” alloy [1]. Heusler alloys are ferromagnetic alloys based on a Heusler phase, which is an intermetallic phase (a solid phase containing two or more metals) with face-centered-cubic structure. O’Handley et al. were able to induce reversible deformations of $0.2 %$ by application of magnetic fields below $1 T$ . Since then, the study of Heusler alloys with magnetic shape-memory properties has become an active field of research with great richness of basic physics, together with technologically interesting possibilities for applications, such as sensors and actuators.

Only a few years after the effect was proposed, giant deformations of about $10 %$ were obtained in similar compounds of a slightly different, nonstoichiometric composition [2], and currently, much effort is expended in search of new Heusler materials with improved properties. At present, it is known that almost any $Ni-Mn$ -based Heusler alloy will show a martensitic transition at an appropriate off-stoichiometric composition. In addition, these materials show other interesting functional properties such as magnetoresistance [3] or magnetocaloric effects [4]. The complex behavior displayed by these materials is, to a large extent, a consequence of the strong coupling between magnetism and structure that arises from the martensitic transition as the sample is cooled. Now, in a paper published in Physical Review Letters, Mao Ye and Akio Kimura at Hiroshima University, together with collaborators at Tohoku University, the National Institute for Materials Science, and Tohoku Gakuin University, all in Japan, study the case of ${Ni}_{2} {Mn}_{1 + x} {Sn}_{1 - x}$ alloys to elucidate the role of excess $Mn$ ions in driving the martensitic transition [5].

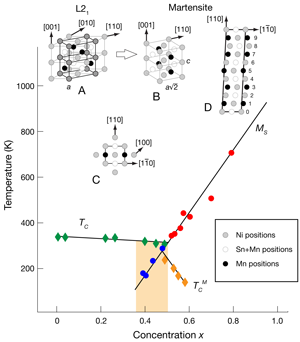
Stoichiometric Heusler alloys have a generic formula $X_{2} Y Z$ and display an $L 2_{1}$ structure at high temperature (see structure A, Fig. 1). The magnetism is due to $3 d$ electrons from $X$ and/or $Y$ elements. The martensitic transition is a first-order, diffusionless transition that occurs via a dominant shear mechanism. The actual final martensitic structure depends on the alloy composition. The observed structures can be described as modulated phases that, to a good approximation, can be constructed from nanotwinned variants of a tetragonal $L 1_{0}$ phase (resulting in crystal structure D in Fig. 1, after twinning) [6]. In $Ni-Mn$ - $Z$ (where $Z = Ga, In, Sn, Sb$ , …), there is a composition range where, on cooling, the system first becomes ferromagnetic, and at a lower temperature undergoes the martensitic transition. Unless the $Z$ chosen is $Ga$ , this range is very narrow and is located in the $Mn$ -rich region. For $Ni-Mn-Ga$ , the range is very broad and extends from the $Mn$ -poor to the $Mn$ -rich regions (see, for instance, Ref. [7]). ${Ni}_{2} MnGa$ is so far the only known stoichiometric Heusler alloy that shows a martensitic transition in the ferromagnetic state.

In $Ni-Mn$ -based alloys, it can be assumed that magnetic moments are localized at $Mn$ atoms that are magnetically coupled through an oscillatory interaction via conduction electrons. Consequently, the magnetic behavior of these alloys is extremely sensitive to the distance between $Mn$ atoms [8,9] and shows some dependence on the $Z$ constituent. In general, however, for compositions with excess $Mn$ , the magnetic moment decreases at the transition on cooling due to closer-neighbors $Mn-Mn$ positions (Fig. 1), which become antiferromagnetically coupled [10]. Furthermore, for some compositions a re-entrance into a paramagnetic martensitic phase has been observed [11]. The significant decrease in magnetization at the transition favors the possibility of inducing the reverse transition magnetically, thus enabling the occurrence of magnetic superelasticity [12,13].

A good control of the parameters that govern phase stability is necessary to optimize materials design and to improve their functional properties. This requires an in-depth knowledge of the complex microscopic mechanism driving the martensitic transition in these ferromagnetic Heusler alloys, and thus a deep understanding of the behavior of the electronic structure in the vicinity of the transition. While several theoretical approaches have been reported, experimental work lags behind. Recently, uv-photoemission measurements in a nearly stoichiometric ${Ni}_{2} MnGa$ single crystal have been reported [14]. At the intermediate premartensitic transition, results confirm a depletion of electronic states (formation of a shallow pseudogap) located slightly below the Fermi energy ( $0.3 eV$ ) associated with the reconstruction of $Ni 3 d$ minority spin-electron states, as predicted by theory [15]. On further cooling, at the martensitic transition, the peak associated with the $Ni 3 d$ minority spin-electrons disappears and the spectral weight shifts to slightly higher energies ( $0.8 eV$ ). This shift reflects $Ni 3 d$ and $Mn 3 d$ electronic contributions to the spin-up density of states. This is usually understood as a band Jahn-Teller mechanism and suggests a charge-density wave mechanism from Fermi surface nesting [15].

The paper by Ye et al. has extended the study of the role of electronic structure in martensitic transition of ferromagnetic Heusler systems to the case of ${Ni}_{2} {Mn}_{1 + x} {Sn}_{1 - x}$ alloys by combining hard x-ray photoelectron spectroscopy and first-principle calculations [5]. The interest in these new results arises from the fact that the authors have explicitly considered the relevance of the excess $Mn$ in driving the martensitic instability by investigating systems of selected compositions. The obtained temperature-dependent photoemission spectra show an abrupt decrease of the peak associated with minority $Ni 3 d$ states at the martensitic transition (which occurs for $x \geq 0.36$ ). This is associated with a band splitting that decreases the total energy, thus stabilizing the lattice distortion associated with the transition. This corroborates the expectation that the martensitic instability is related to a band Jahn-Teller mechanism.

Perhaps more interesting is the fact that the high-temperature peak associated with $3 d$ minority spins shows a systematic shift towards the Fermi energy when the excess $Mn$ concentration increases from $x = 0$ to $0.42$ . This shift nicely correlates with a decrease of lattice parameter of about $2 %$ . The first-principle calculations of Ye et al. attribute the shift of the peak to the hybridization of $Ni 3 d$ and $3 d$ states of antiferromagnetically coupled $Mn$ atoms located at $Sn$ sites. These results demonstrate that excess $Mn$ enables hybridization of electronic states that strongly affect the stability of the martensitic phase in $Ni-Mn-Sn$ Heusler alloys. In contrast, it is worth noticing that the excess $Mn$ has very little effect on the temperature at which the $L 2_{1}$ phase becomes ferromagnetic.

Comparison of the results obtained in ${Ni}_{2} MnGa$ and $Ni-Mn-Sn$ clearly reveals the importance of the $Z$ constituent on the behavior of these Heusler shape-memory alloys. The relevance of the $Z$ element on the stability range of the martensitic phase in $Ni-Mn$ -based Heusler alloys has also been pointed out in Ref. [16]. From present photoemission results, one can speculate that the extent of hybridization between $Mn$ and $Ni$ electronic states that establishes the range of stability of the martensitic phase depends crucially on the choice of $Z$ element. It is only in the case of $Z$ as $Ga$ that off-stoichiometry composition is not needed for the transition to occur. For compositions close to the $2$ - $1$ - $1$ stoichiometry, when hybridization does not play a role, the instability towards the martensitic phase occurs in a two-step process through an intermediate martensitic phase at which a pseudogap is formed in the density of states. This requires Fermi surface nesting effects that seem to be optimized for a given high enough value of the magnetization [17]. Indeed, recent finite temperature first-principle calculations suggest that this premartensitic instability is only possible thanks to a delicate interplay between magnetic excitations that overcompensate vibrational entropy [18].

The latest results from Ye et al. are likely to open new avenues of investigation of the basic physics underlying magnetic shape-memory phenomena as well as other complex functional materials where electronic instabilities are usually responsible for emergent functionalities. Moreover, these results are expected to provide insight into the more general phenomenon of magnetoelasticity.

References

K. Ullakko, J. K. Huang, C. Kantner, R. C. O’Handley, and V. V. Kokorin, Appl. Phys . Lett. 69, 1966 (1996)
A. Sozinov, A. A. Likhachev, N. Lanska, and K. Ullakko, Appl. Phys . Lett. 80, 1746 (2002)
C. Biswas, R. Rawat, and S. R. Barman, Appl. Phys . Lett. 86, 202508 (2005)
A. Planes, L. Mañosa, and M. Acet, J. Phys. Condens. Matter 21 233201 (2009)
M. Ye, A. Kimura, Y. Miura, M. Shirai, Y. T. Cui, K. Shimada, H. Namatame, M. Taniguchi, S. Ueda, K. Kobayashi, R. Kainuma, T. Shishido, K. Fukushima, and T. Kanomata, Phys. Rev. Lett. 104, 176401 (2010)
S. Kaufmann, U. K. Rößler, O. Heczko, M. Wuttig, J. Buschbeck, L. Schultz, and S. Fälher, Phys . Rev. Lett. 104, 145702 (2010)
P. Entel, V. D. Buchelnikov, M. E. Gruner, A. Hucht, V. V. Khovailo, S. K. Nayak, and A. T. Zayak, Mater. Sci. Forum 583, 21 (2008)
E. Sasioglu, L. M. Sandratskii, and P. Bruno, Phys . Rev. B 70, 024427 (2004)
V. D. Buchelnikov, V. V. Sokolovskiy, H. C. Herper, H. Ebert, M. E. Gruner, S. V. Taskaev, V. V. Khovaylo, A. Hucht, A. Dannenberg, M. Ogura, H. Akai, M. Acet, and P. Entel, Phys. Rev. B 81, 094411 (2010)
S. Aksoy, M. Acet, P. P. Deen, L. Mañosa, and A. Planes, Phys. Rev. B 79, 212401 (2009)
R. Y. Umetsu, R. Kainuma, Y. Amako, Y. Taniguchi, T. Kanomata, K. Fukushima, A. Fujita, K. Oikawa, and K. Ishida, Appl. Phys. Lett. 93, 042509 (2008)
R. Kainuma, Y. Imano, W. Ito, Y. Sutou, H. Morito, S. Okamoto, O. Kitakami, A. Fujita, T. Kanomata, and K. Ishida, Nature 439, 957 (2006)
T. Krenke, E. Duman, M. Acet, E. F. Wassermann, X. Moya, L. Mañosa, A. Planes, E. Suard, and B. Ouladdiaf, Phys . Rev. B 75, 104414 (2007)
C. P. Opeil, B. Mihaila, R. K. Schulze, L. Mañosa, A. Planes, W. L. Hults, R. A. Fisher, P. S. Riseborough, P. B. Littlewood, J. L. Smith, and J. C. Lashley, Phys . Rev. Lett. 100, 165703 (2008)
A. Ayuela, J. Enkovaara, and R.M. Nieminen, J. Phys . Condens. Matter 14, 5325 (2002)
T. Krenke, X. Moya, S. Aksoy, M. Acet, P. Entel, L. Mañosa, A. Planes, Y. Elerman, A. Yücel, and E. F. Wassermann, J. Magn. Magn. Mater. 310, 2788 (2007)
Y. Lee, J. Y. Rhee, and B. N. Harmon, Phys . Rev. B 66, 054424 (2002)
M. A. Uijttewaal, T. Hickel, J. Neugebauer, M. E. Gruner, and P. Entel, Phys. Rev. Lett. 102, 035702 (2009)

About the Author

Dr. Antoni Planes is a Professor of Physics in the Department d’Estructura i Constituents de la Matèria at the Universitat de Barcelona, Catalonia, where he leads a group in phase transitions. His recent research has focused on the study of phase transitions in systems with interplay between structure and magnetism, such as magnetic shape-memory and magnetocaloric materials. He is also active in the study of the influence of disorder in phase transitions, with the aim of understanding precursor phenomena and avalanche criticality in externally driven systems.

Role of Electronic Structure in the Martensitic Phase Transition of ${Ni}_{2} {Mn}_{1 + x} {Sn}_{1 - x}$ Studied by Hard-X-Ray Photoelectron Spectroscopy and Ab Initio Calculation

M. Ye, A. Kimura, Y. Miura, M. Shirai, Y. T. Cui, K. Shimada, H. Namatame, M. Taniguchi, S. Ueda, K. Kobayashi, R. Kainuma, T. Shishido, K. Fukushima, and T. Kanomata

Phys. Rev. Lett. 104, 176401 (2010)

Published April 26, 2010

Read PDF