Ultrafast computing with molecules

Ian Walmsley

Viewpoint

Ultrafast computing with molecules

Clarendon Laboratory, Department of Physics, University of Oxford, Oxford OX1 3PU, UK

May 3, 2010• Physics 3, 38

Vibrations of the atoms in a molecule are used to implement a Fourier transform orders of magnitude faster than possible with devices based on conventional electronics.

Figure caption — **Figure 1:** (a) Phase space dynamics of a molecular vibrational harmonic oscillator. Time evolution is equivalent to a rotation of the phase space. The Wigner function representing the vibrational quantum state is shown at two different times differing by a quarter of the vibrational period. Measurement of the position of the vibrational wave packet is equivalent to projection of the Wigner function onto the coordinate axis. The two marginal distributions shown (lines) indicate the origin of the Fourier transform, since they are proportional to the initial probability distributions of the position and momentum probability of the wave packet. (b) The diatomic molecule is excited from the ground to the first excited electronic state by a shaped optical program pulse (P) that prepares the initial quantum state of the vibrational mode—effectively programming the distribution to be Fourier transformed. A quarter vibrational period later, a reference pulse (R), generates a second vibrational wave packet that interferes with the first, converting the accumulated phase into populations of vibrational levels in the excited state. A measurement laser (M) reads out the populations by inducing transitions to a higher-lying electronic state, from which fluorescence (f) is detected. The fluorescence intensity is proportional to the population in the vibrational level to which the measurement laser is tuned.

The intimate connection between information and physics has received considerable emphasis in the past two decades, in large part due to the stunning successes of quantum information science (QIS). This has led to the exploration of a wide variety of physical platforms that may be adapted for implementing useful information-processing protocols. Among these are atoms, ions, molecules, photons, superconductors, and semiconductors.

The focus of QIS is on capabilities for computing, communications, and metrology that transcend those of devices designed using principles of classical physics. The emergence of this field has led, in addition, to considerations of whether classical information processing may be enhanced by making use of new physical instantiations, even when the full power of multiparticle quantum correlations are not used [1,2]. Writing in Physical Review Letters, Kouichi Hosaka [3] and collaborators from several institutions in Japan illustrate how quantum interference may be used to execute a common classical algorithm very rapidly—within a few tens of femtoseconds. Hosaka et al. demonstrate that the dynamics associated with the vibrations of the atoms in a molecule can be used to implement a Fourier transform. The rapidity of the molecular oscillations means that this protocol can be executed very quickly—much quicker, as the authors point out, than any conceivable device based on conventional electronics.

The physics underlying the algorithm is simple and elegant. The vibrational mode of a diatomic molecule, when excited close to equilibrium, approximates an isolated harmonic oscillator. If the molecule is well isolated from its environment, and at a low temperature, the oscillator experiences very little decoherence either from collisions, or by the coupling of the vibrational and rotational motion, so that the unitary evolution necessary for the effect is dominant.

A remarkable feature of the quantum harmonic oscillator is that the dynamical evolution of a wave packet is exactly that of a fractional Fourier transform, with the complete transform occurring periodically at times $t = t_{0} + (2 n + 1) π / 2 ω$ , ( $n = 0, 1, 2 \dots$ ), where $t_{0}$ is an initial reference time. Therefore the wave packet one-quarter period after initial preparation is the Fourier transform of the original wave packet:

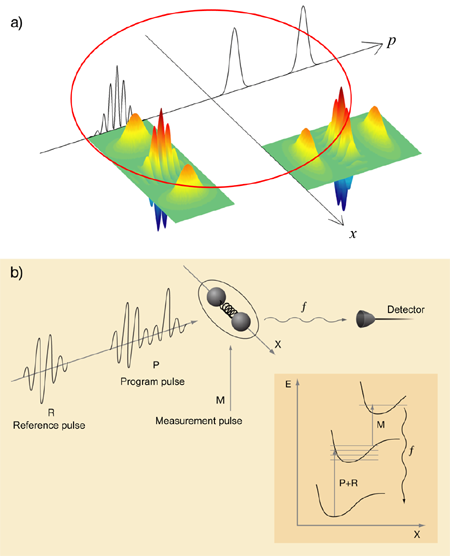
An alternative way to see this is in terms of a phase-space picture of the motion, as illustrated in Fig. 1 (a).

The Wigner function $W_{ψ} (x, p; t)$ of the wave packet provides a convenient representation of its quantum state, simultaneously encoding joint information about the position $x$ and momentum $p$ of the oscillator. It is a joint quasiprobability density function, the marginals of which are the probability distributions of the particle’s position or momentum. This function follows a circular trajectory through the phase space of the oscillator, as indicated in the Fig. 1, and the dynamics are simply described by rotations of the Wigner distribution about the origin.

It is clear from this picture that a measurement of the position of the oscillator, indicated by the projection of the Wigner function onto the position axis of the phase space, will transform between that of the initial position distribution and the initial momentum distribution every quarter period. This feature has been recognized as enabling a number of useful applications. For example, the fractional Fourier transform implemented at times between $t$ and $t = t_{0} + π / 2 ω$ suggests that sufficient information can be obtained to completely reconstruct the quantum state of the oscillator [4,5].

In the present paper, the authors now use these dynamics to effect a discrete Fourier transform. A vibrational wave packet is generated in an iodine molecule by exciting the electronic transition to which the vibrational mode is coupled. With the electron in the excited state, the atoms are no longer in equilibrium and begin to oscillate. The vibrational quantum state can be adjusted by changing the temporal shape of the optical pulse that excites the electron—shaking the electron in a carefully controlled way enables the shape of the molecular vibrational wave packet to be sculpted.

The transformed wave packet is measured by means of a two-step process [see Fig. 1 (b)]. First, a reference wave packet, generated in a similar manner to the program pulse by a separate reference laser pulse, is added. This has the effect of changing the amplitudes of the vibrational eigenstates making up the wave packet in proportion to the phase they have accumulated in their free evolution. The particular mechanism for this is that the molecular states may be excited or de-excited, depending on the relative phase of the electronic dipole excited by the first pulse with respect to the electric field of the second pulse. Once this phase-to-amplitude transfer has occurred, the amplitudes of the individual vibrational states are measured by exciting them to a higher electronic state using a separate narrow band probe laser. The fluorescence from these states is measured as a function of the wavelength of the probe laser and as a function of the phase of the reference laser pulse. This gives the eigenstate populations as the probe laser is tuned through the appropriate energy level, from which the phases may be inferred and the wave packet evolution determined.

The authors point out the important feature that the molecular motion executes the Fourier transform in a mere $145 fs$ . This is several orders of magnitude faster than devices based on silicon electronics are likely to be able to achieve. This observation provokes an enticing proposition—the idea of high-speed, nondissipative logic operations and algorithms would make for a revolution in physical instantiations of computational devices.

However, there are a number of important barriers that will need to be overcome if such devices are to displace current high-speed electronics. First, the programming and readout of the device necessarily require significant resources, both in actual implementation and in principle. This overhead would need to be reduced dramatically for such an approach to be feasible in practice. Second, the connectivity required for implementing large-scale processors is missing. It is not yet possible to string together a sequence of these Fourier transformers with other operations in between in a way that enables a real programmable device to be constructed. Third, this approach does not embrace the favorable scaling of the device that is the hallmark of quantum information processors. This is because the protocol makes use of single-particle interference—a quantum effect to be sure, but one which has analogs in classical wave physics. The use of a molecular valence electron to control and to readout the vibrational state means that the approach lacks the multiparticle entanglement needed to realize exponential improvements on current computational capacity. Recognizing the key element involved as single-particle quantum interference raises the question as to whether a process based on wave interference might well be simulated entirely optically in an equally efficient manner [6,7].

Nonetheless, the notion of a classical processor with such a dramatic speed-up suggests that it is worth continuing to explore new ways to use physical systems to encode and manipulate information, and that this connection may reveal new insights into both physics and into information processing.

References

J. Ahn, T. C. Weinacht, and P. H. Bucksbaum, Science 287, 463 (2000)
M. N. Leuenberger and D. Loss, Nature 410, 789 (2001)
K. Hosaka, H. Shimada, H. Chiba, H. Katsuki, Y. Teranishi, Y. Ohtsuki, and K. Ohmori, Phys. Rev. Lett. 104, 180501 (2010)
T. Dunn, I. A. Walmsley, and S. Mukamel, Phys. Rev. Lett. 74, 884 (1995)
U. Leonhardt and M. G. Raymer, Phys. Rev. Lett. 76 1985 (1996)
E. Brainis et al., Phys. Rev. Lett. 90, 157902 (2003)
P. Londero, C. Dorrer, M. Anderson, S. Wallentowitz, K. Banaszek, and I. A. Walmsley, Phys. Rev. A. 69, 0103029 (2004)

About the Author

Ian Walmsley is the Hooke Professor of Experimental Physics at the University of Oxford, where he is also the Pro-Vice Chancellor for Research. He was formerly the Head of Atomic and Laser Physics at Oxford, and served as Director of the Institute of Optics at the University of Rochester in the US. His research is in the area of optical science and engineering, and he is particularly interested in the applications of quantum optics to novel photonic technologies, as well as the control of quantum systems. He has contributed particularly to the development of methods for quantum tomography and in a different sphere to methods for the complete characterization of ultrashort optical pulses, inventing the SPIDER technique. He is a fellow of the Optical Society of America, the American Physical Society, and the UK Institute of Physics, and leads a number of research collaborations, including an EU Integrated Project on Qubit Applications. In 2008, Dr. Walmsley was named an Outstanding Referee by the American Physical Society.