Is there a true supersolid phase transition ?
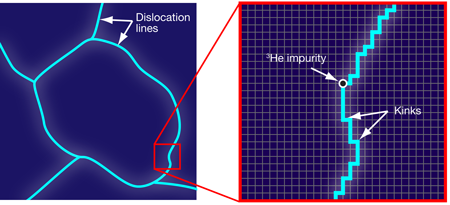
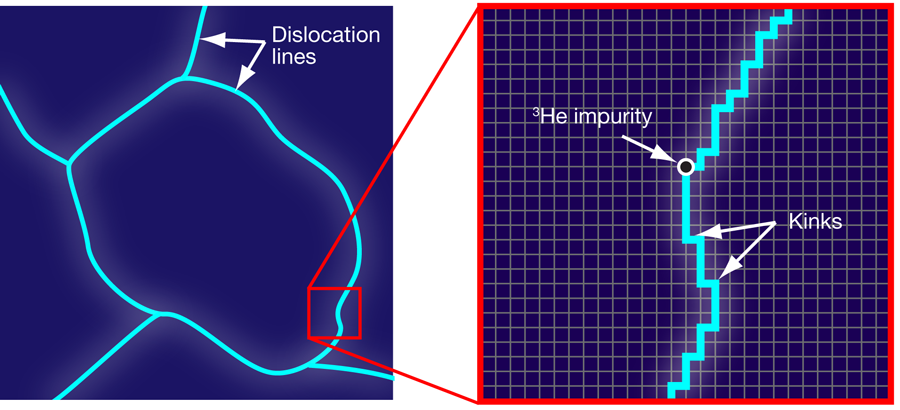
Six years have passed since Kim and Chan [1,2] discovered supersolidity when they found that solid 4He does not rotate like a classical solid. Despite substantial effort, however, this phenomenon is not yet understood [3]. Some probably think that the research on this puzzling issue is too slow. Others, including myself, enjoy every new controversy and every new advance as if they were reading a detective story. In this tale, the latest twist is a study reported in Physical Review Letters by Oleksandr Syshchenko, James Day, and John Beamish at the University of Alberta, Canada [4], of the shear modulus of solid 4He in the temperature range where it becomes supersolid. They confirm that the observed change in stiffness is associated with a binding of dislocations to 3He impurities (Fig. 1) when the solid is cooled down (then unbinding when warming up, of course) and they show now that this binding is gradual because there is a rather wide distribution of binding energies. Why is this so important?
As is now well known, supersolidity means a coexistence of superfluid and solid behaviors. This is surprising but possible, especially if the solid under consideration has disorder, for example, dislocations [5]. Even more surprising was probably the discovery by Day and Beamish [6] in 2007 that solid helium is stiffer in its supersolid phase than in its normal phase. Moreover, the variation of the elastic shear modulus as a function of temperature was shown to be exactly the same as that of the rotational inertia. The two properties must be consequences of a single phenomenon, but which one? This is what all of the researchers in this field are trying to understand.
Day and Beamish had also shown that, near the transition, the elastic modulus has a much larger variation than the rotational inertia. The typical variation of the modulus is 10% in polycrystalline samples instead of only 1% for the inertia. Now, Syshchenko et al. [4] show that the elastic properties can also be studied in a wide range of frequencies—from 0.5 Hz to 8 kHz—while the study of the rotational inertia in torsional oscillators is restricted to a few hundred hertz around 1 kHz. They took advantage of that to study the nature of the transition from the normal to the supersolid state. Some authors had tried to fit variations as a function of temperature with power laws and critical exponents, as is usually done close to phase transition temperatures [7]. But this work shows that the latter approach is not appropriate. The onset of the transition is broad because the binding energies of dislocations to 3He impurities are distributed around a temperature of 0.73 K with a large width ( 0.45 K). It is a crossover in a thermally activated process and, according to Syshchenko et al.: “if there is a true phase transition … it must be at lower temperature.”
Is there a “true phase transition” then? Syshchenko, Day, and Beamish probably have their own thoughts on the matter, but they are careful and do not answer this fundamental question. However, I will attempt an answer of my own. One needs to understand first why there is a coupling between rigidity and supersolidity. The reason why helium crystals are stiffer at low temperature, say 20 mK, than at higher temperature, say 200 mK, is that a crystal with fixed dislocations is stiffer than a crystal with mobile dislocations. This is actually well known in materials science [8]. So I propose the following scenario: Inside the core of dislocations, the atoms are not densely packed, and that is actually why atom exchange is much easier there than in the bulk of the crystal, something which may lead to quantum coherence and superfluidity. But if the dislocations are mobile, they have transverse fluctuations, that is, fluctuations of their position and consequently of their total length if their ends are fixed. As a result, there should be fluctuating mass currents. In a quantum coherent system, mass currents are proportional to the gradient of the phase of the wave function so that these fluctuations should induce phase fluctuations and this should kill the quantum coherence that is necessary for supersolidity.
My intuition is that a fluctuating dislocation cannot be supersolid. On the contrary, if a dislocation is supersolid, the phase of the wave function must be locked and the dislocation a fixed line. This is how I understand that the stiffness transition in helium crystals is closely linked to their supersolid transition. When the dislocations are pinned by 3He impurities, that is, at low temperature, they form a network of supersolid lines throughout the whole solid, but if the dislocations unpin, they fluctuate and supersolidity disappears. If my physical intuition is correct, the dislocation pinning controls the whole phenomenon. In this picture, the onset of the phenomenon may be broad, as observed by Syshchenko et al., but as the temperature is lowered, all dislocations progressively stop fluctuating and a quantum coherence should set in and percolate through the whole network of dislocations, ending with a “true phase transition” to a supersolid state. This must be the origin of the peak in the specific heat that has been measured by Lin et al. [9]. Now how to check this picture?
Last year, my colleagues and I had shown that it is possible to suppress all 3He impurities [10], but we doubt that this is sufficient to free all dislocations at all temperatures and suppress supersolidity. Indeed, we have also found that, in ultrapure samples, the “crossover” to a stiff state—I do not call it a transition anymore—is displaced to lower temperature (less than 40 mK) but perhaps not suppressed [11]. One possible interpretation of this can be found in an article by Aleinikava et al. [12] who explained in 2010 that the dislocations could be pinned not only by 3He impurities but also by the crystal lattice itself (its so-called “Peierls potential”). There should be a roughening transition of the dislocations lines, which should depend on the presence of impurities but is not suppressed in their absence. Given all these other results and in order to check the dislocation scenario for supersolidity, the thing to do is to suppress not only impurities but also dislocations in single crystals and see if supersolidity disappears. It should—except if a totally different scenario is at work, for example, the proliferation of vortices, which is proposed by Anderson [13] and was recently presented as supporting their study of relaxation times by Kim et al. [14]. We will see. I actually expect another controversy to come up as a result of a very recent article by Reppy [15] in which he presents measurements in a highly disordered sample that are incompatible with supersolidity. In view of this, I am afraid that our detective story is far from finished.
References
- E. Kim and M. H. W. Chan, Nature 427, 225 (2004)
- E. Kim and M. H. W. Chan, Science 305, 1941 (2004)
- For a recent review and see S. Balibar, Nature 464, 176 (2010)
- O. Syshchenko, J. Day, and J. Beamish, Phys. Rev. Lett. 104, 195301 (2010)
- M. Boninsegni, A. B. Kuklov, L. Pollet, N. V. Prokof’ev, B. V. Svistunov, and M. Troyer, Phys. Rev. Lett. 99, 035301 (2007)
- J. Day and J. Beamish, Nature 450, 853 (2007)
- A. C. Clark, J. West, and M. H. W. Chan, Phys. Rev. Lett. 99, 135302 (2007)
- J. Friedel, Dislocations (Pergamon Press, Oxford, 1964)
- X. Lin, A. C. Clark, and M. H. W. Chan, Nature 449, 1025 (2007); X. Lin, A. C. Clark, Z. G. Cheng, and M. H. W. Chan, Phys. Rev. Lett. 102, 125302 (2009)
- C. Pantalei, X. Rojas, D. O. Edwards, H. J. Maris, and S. Balibar, J. Low Temp. Phys. 159, 452 (2010)
- X. Rojas, C. Pantalei, H. J. Maris, and S. Balibar, J. Low Temp. Phys. 158, 478 (2010)
- D. Aleinikava, E. Dedits, A. B. Kuklov, and D. Schmeltzer, Europhys. Lett. 89, 46002 (2010)
- P. W. Anderson, Nature Phys. 3, 160 (2007)
- H. Choi, S. Kwon, D. Y. Kim, and E. Kim, Nature Phys. 6, 4 April (2010)
- J. D. Reppy, arXiv:1004.1129