Blurry vision belongs to history
The classical view that lens-based optical microscopes cannot resolve details separated by less than half the wavelength of light is increasingly becoming a dated one. Several microscopy techniques, used either alone or in combination, can now beat the diffraction limit by at least a factor of 2. Now, in a paper appearing in Physical Review Letters, Claus Müller and Jörg Enderlein at Georg August University in Göttingen, Germany, add to this arsenal of techniques a method that essentially involves modifying an existing bench-top confocal-laser scanning microscope [1]. This type of microscope—called a CLSM for short—is already a fundamental tool for research, particularly in the biological sciences, and Müller and Enderlein’s proposal could influence a broad community.
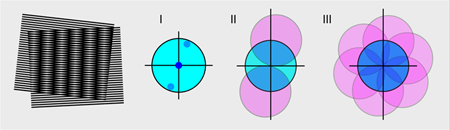
Müller and Enderlein’s technique is built on the method of structured illumination microscopy [2]. When two fine patterns—like that of two combs with different teeth spacing—superimpose multiplicatively, they create moiré fringes (Fig. 1, left). In the case of structured illumination, one pattern is the fluorescence of an unknown sample, while the other pattern comes from the “structured illumination” source, which has a known spatial dependence. The product of the sample and the illumination patterns generates an image that has spatial frequencies that are both sum and difference frequencies between those contained in the original patterns. The difference frequencies, which make up the moiré fringes, have a lower spatial frequency than either of the original patterns and it is these fringes that can often be resolved by a microscope, even if the spatial frequencies of the original patterns themselves are too high to be resolved (see the sequence of panels on the right of Fig. 1).
To extract the unknown sample pattern, one needs to do the Fourier back-transformation from frequency space to real space, including a “filter function” that takes the illumination pattern into account. Structured illumination can resolve objects a factor of 2 better than expected from the classical optical resolution limit and, experimentally, the approach is relatively straightforward. The main challenge lies in the Fourier analysis of the image.
When a wide area of the sample is illuminated, the structured illumination approach is conceptually clear and well established [2]. Müller and Enderlein’s insight was to realize that a diffraction-limited laser focus is itself a special type of structured illumination, containing all possible Fourier modes allowed by the confocal microscope. In order to image the entire spatial pattern of the fluorescence generated by such a laser excitation, that is, the convoluted image of the laser focus and the sample, Müller and Enderlein use a CCD camera in place of the point detector found in conventional confocal-laser microscopes. At each point in the laser’s scan across the sample, an image is captured on the CCD camera, which, like the moiré fringes in Fig. 1, contains the information of the spatial distribution of the illumination (the laser focus) and the local sample pattern. Now, if one knows the spatial distribution of the laser focus, it is possible to filter out the unknown sample pattern from the CCD image, improving the resolution by up to a factor of 2. Although this gain in resolution is moderate, it is enough to enter dimensions where important biological questions await answers. Müller and Enderlein’s technique is also, in contrast to some others, simple. In principle, most confocal-laser scanning microscopes could be adapted to take advantage of the intrinsic structured illumination in the laser focus.
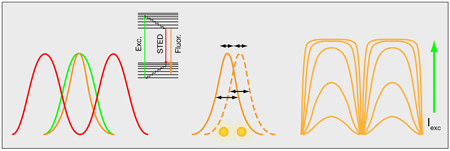
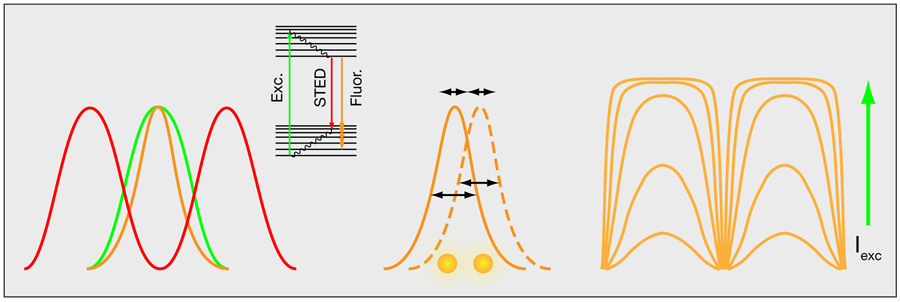
In a more general perspective, structured illumination microscopy—either in the wide-field approach or that proposed by Müller and Enderlein—is just one out of several tricks that have proven extremely useful for enhancing far-field optical resolution. An important example is the resolution enhancement that comes from combining controlled photoswitching of fluorescent molecules with the nonlinear fluorescent response of molecules to high-intensity light. This is the principle behind stimulated emission by depletion (STED) microscopy [3]. In STED microscopy, an additional irradiance field is applied in the peripheral parts of the excitation field to drive fluorescent molecules into a dark ground state by stimulated emission (Fig. 2, left). Similar effects can be accomplished by using other photo-induced states [4].
Another way to improve the resolution takes advantage of the fact that the intensity profiles of single fluorescent molecules can be determined with high precision. Optical resolution limits the width of these profiles, but their peak intensities can be determined with a precision far beyond the classical resolution limit [5]. By switching the fluorescent molecules on and off with light, the location of a few, spatially well-separated, individual molecules can be determined at a time (Fig. 2, middle). Repeating this process and overlapping images of many individual molecules can generate an image of even densely labeled samples [6,7].
Finally, there is a way to enhance the resolution of structured illumination (at least theoretically) by an unlimited amount. The idea takes advantage of the nonlinear photophysical response of fluorescent molecules [8,9]. At low intensities, the pattern of fluorescence in the sample will follow that of the illumination, but as the illumination intensity increases, molecules experiencing the most intense illumination will saturate (Fig. 2, right). For example, a sinusoidal illumination pattern will produce a squarelike pattern of fluorescence in the sample, which basically contains all Fourier frequencies, from the most fundamental frequencies to frequencies far beyond those that are observable. Although these latter frequencies cannot be detected, their contribution is known from the saturation behavior of the fluorophores and it is possible to reconstruct images over a wider spatial frequency range and with a correspondingly increased spatial resolution.
Müller and Enderlein point out that one could also take advantage of saturation effects in their approach. Moreover, it should be possible to adapt any existing confocal-laser scanning microscope to follow their technique, even incorporating standard features on the microscope, such as multicolor imaging and a three-dimensional sectioning.
Müller and Enderlein’s method is one out of several important recent contributions to the very active development of ultrahigh resolution far-field optical imaging. This development, based on the interplay between optics and photophysical spectroscopy, has still not come to an end. Simultaneously with this work, the use of laser scanning microscopy for structured illumination has also been suggested for high-resolution two-photon fluorescence microscopy [10]. Indeed, spatially varying illumination patterns of a laser focus for resolution enhancement could possibly also be based on other nonlinear spectroscopic transitions, not necessarily involving fluorescence generation, for instance, stimulated Raman spectroscopy or photothermal spectroscopy. Overall, the ongoing development in high-resolution optical microscopy will virtually open, or rather sharpen, the eyes of the observers in many research fields, most notably in biology, where a wealth of relevant structures and interactions fall beyond the classical resolution limits of light microscopy.
References
- C. B. Müller and J. Enderlein, Phys. Rev. Lett. 104, 198101 (2010)
- M. G. L. Gustafsson, J. Microsc. 198, 82 (2000)
- S. W. Hell and J. Wichmann, Opt. Lett. 19, 780 (1994)
- S. W Hell, Science 316, 1153 (2007)
- W. Heisenberg, The physical principles of the quantum theory (Dover Publications, New York, 1930)[Amazon][WorldCat]
- M. J. Rust et al., Nat. Methods 3, 793 (2006)
- E. Betzig et al., Science 313, 1642 (2006)
- R. Heintzmann et al., J. Opt. Soc. Am. A 19, 1599 (2002)
- M. G. L. Gustafsson, Proc. Natl. Acad. Sci. USA 102, 13081 (2005)
- J. Lu et al., Nano Lett. 9, 3883 (2009)