Supersolidity or quantum plasticity?

John Beamish

Viewpoint

Supersolidity or quantum plasticity?

Department of Physics, University of Alberta, Edmonton, Alberta T6G 2G7, Canada

June 21, 2010• Physics 3, 51

New torsional oscillator experiments with plastically deformed helium show that what was thought to be defect-controlled supersolidity at low temperature may in fact be high-temperature softening from nonsuperfluid defect motion in the crystalline structure.

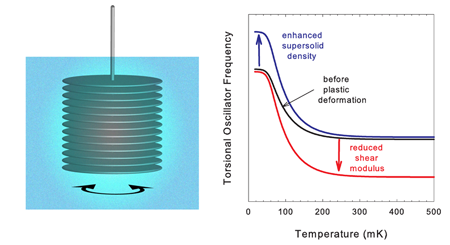
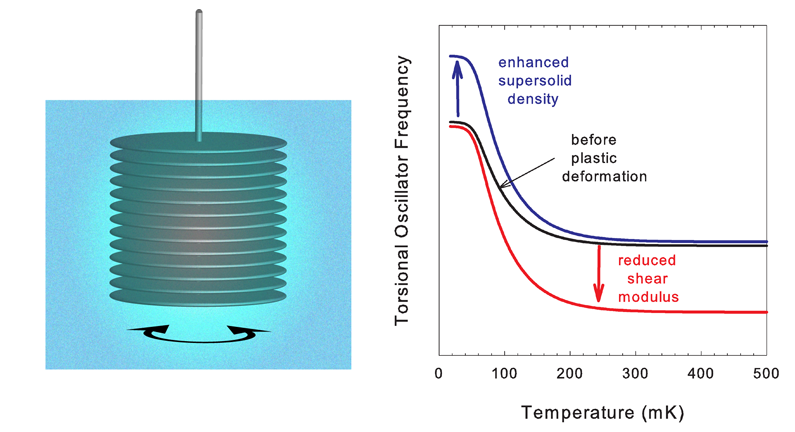
Figure caption — **Figure 1:** (Left) Andronikashvili torsional oscillator. Viscous fluid is dragged by the moving disks, increasing the moment of inertia and reducing the oscillation frequency. In the superfluid phase, there is a frictionless component that does not move with the disks. The decoupling of this mass raises the oscillator frequency, giving a direct measurement of the superfluid density. (Right) What happens when solid helium is plastically deformed? Black curve: torsional oscillator frequency before deforming the helium. The increase at low temperatures suggests decoupling of some of the solid helium, i.e., supersolidity. Blue curve: the expected behavior if the defects produced by deformation enhance the supersolid fraction. Red curve: the behavior if the effect of the new defects is to elastically soften the crystal.

Superfluidity—the frictionless flow of a liquid analogous to lossless current flow in a superconductor—is well known in liquid $^{4} He$ , but “supersolidity”—coexistence of crystalline order and superflow—seems counterintuitive. However, quantum mechanics allows atomic exchange even in a solid, especially if the atoms are light and the interatomic potential is weak. This makes helium the most quantum of solids and the possibility of supersolidity in helium was suggested more than 40 years ago [1]. Despite earlier searches, it was not until 2004 that Kim and Chan’s torsional oscillator experiments [2,3] provided convincing evidence of supersolidity. The torsional oscillator technique has been a cornerstone of our understanding of superfluidity since Andronikashvili’s classic experiment [4] in which he attached immersed disks in liquid $^{4} He$ and set them into torsional oscillation (Fig. 1, left) . Liquid moving with the discs contributed to the oscillator’s moment of inertia and so reduced its frequency (increased its period). Since a frictionless fluid is not dragged along with the disks, the oscillator frequency provided a direct measurement of the superfluid density in liquid helium. During the 1970s, John Reppy and co-workers at Cornell University in the US refined the “high $Q$ torsional oscillator” into an exquisitely sensitive tool for studying superfluids. Now, Reppy reports new experiments in Physical Review Letters [5] that throw into question our current understanding of supersolidity.

Reppy describes the first experiments in which solid helium is plastically deformed inside a torsional oscillator. Shearing the crystal parallel to the walls of the oscillator changes its frequency, but only at high temperatures, casting doubt on current ideas that associate defects with supersolidity. Reppy proposes that the observed behavior might be due to elastic softening of crystals by defect motion at high temperatures, rather than to decoupling of a supersolid component at low temperatures. This interpretation is intriguing, but leaves a number of puzzles. As Reppy points out, it does not explain the behavior of helium confined in small pores [2] nor the dependence on quantum statistics [6] ( $^{4} He$ vs $^{3} He$ ). Most importantly, the “blocked annulus” experiment [3], which provides the strongest evidence of long range flow in solid helium, seems to require either superflow or extraordinary elastic properties.

In 2004, Kim and Chan [2,3] repeated the Andronikashvili experiment with solid helium. Using a torsion cell filled with $^{4} He$ at high pressures, they observed an increase in the torsional oscillator frequency below about $200 mK$ , which they interpreted as a superfluidlike decoupling of about $1 %$ of the solid—the “non-classical rotational inertia” (NCRI) that characterizes a supersolid. Two other observations provided important support for this interpretation. First, the apparent decoupling decreased at high oscillation amplitudes, suggesting a critical velocity for superflow, like that seen in superfluid helium. Second, blocking the annular channel eliminated the decoupling, confirming that long range flow was involved. It soon became clear that such supersolidity must involve defects. Rittner and Reppy showed [7] that annealing (which removes defects) dramatically reduced the fraction of the helium that decoupled. Their later experiments [8] showed that the NCRI fraction could be enhanced by growing crystals in narrow channels and by rapid thermal quenching to increase defect densities. Dislocations are created during crystal growth and by plastic deformation and much recent work has focused on the possibility of superflow associated with a dislocation network.

A supersolid might be expected to exhibit other phenomena that characterize superfluids: superleaks, persistent currents, new sound modes, and quantized vortices. Despite much effort, experiments have not yet found such a “smoking gun” and the essential evidence for supersolidity still comes from torsional oscillators. However, elastic measurements [9,10] also show unusual effects that are clearly related to the oscillator behavior. The shear modulus decreases by about $10 %$ upon warming to $200 mK$ , with the same dependence on temperature, amplitude, frequency, and $^{3} He$ impurity concentration as the NCRI. These elastic effects have a natural interpretation in terms of dislocation motion and pinning, but this does not directly involve supersolidity.

An obvious question is raised: are the two phenomena properties of a supersolid state or could changes in the helium’s shear modulus produce the observed torsional oscillator effects without invoking supersolidity? Numerical modelling of several realistic oscillator geometries [11] has shown that the effects of the observed shear modulus changes are much too small—extraordinary softening would be required to account for the apparent NCRI. Nonetheless, the new experiments by John Reppy suggest a nonsupersolid interpretation of the torsional oscillator behavior (Fig. 1, right). Plastic deformation creates dislocations and the higher defect density would be expected to produce a larger supersolid fraction in the helium. The additional mass decoupling would raise the oscillator frequency at low temperature, but would have no effect at high temperatures where there is no supersolid. Reppy’s experiments do not show this behavior. Deformation leaves the frequency unchanged at low temperature but reduces it at high temperatures. Annealing, which removes some defects, has the opposite effect, but again, it is only the high-temperature behavior which changes. Similar behavior is seen in the shear modulus—large strains and annealing both change the shear modulus at high temperatures, but not at low temperature [10]. This is expected for the modulus, since the effect of dislocations is to elastically weaken the crystal when they are mobile (at high temperatures), but not at low temperatures (where they are pinned).

Reppy is the first to plastically deform helium inside a torsional oscillator, but annealing has also been studied by others [12]. Why were the effects of annealing in those experiments interpreted as changes in a supersolid fraction? It is important to realize that the helium makes only a small contribution to the oscillator’s moment of inertia and that the apparent decoupling involves only a small fraction of the helium. The frequency changes associated with the NCRI are typically a few parts per million and must be extracted from a background that depends on temperature. Growing crystals at constant volume (as in most torsional oscillator experiments, including Reppy’s) introduces pressure and density gradients, as well as defects, into the solid helium. Annealing reduces these gradients by redistributing mass within the cell, with corresponding changes in the moment of inertia and oscillator frequency. Annealing also reduces the pressure in the oscillator (by as much as $7$ bar in some of Rittner and Reppy’s earlier work [8]). Depending on how rigid its walls are, these pressure changes can deform the oscillator and affect its frequency. It is not surprising that annealing produces frequency shifts and these have been noted by other groups. Given the focus on supersolid decoupling at low temperatures, it was natural for researchers to compare data by shifting their oscillator frequencies to make the background coincide at high temperatures. Reppy’s measurements suggest that instead it is the low-temperature frequencies that should coincide. However, this does not appear to be the case in all torsional oscillator measurements. In other experiments [13–15], annealing did not change the apparent NCRI but rather shifted the frequency uniformly at all temperatures (up in some experiments, down in others). In other cases, annealing lowered the frequency and also reduced the NCRI.

So what is special about Reppy’s measurements? Is it the design of his cell? His torsional oscillator results differ from measurements by other groups in some other ways. He has seen much larger NCRI fractions ( $6 %$ in this cell, up to $20 %$ in other experiments) and annealing produced more dramatic NCRI and pressure changes than other groups have observed [7,8]. In his current measurements, the narrowness of the annulus ( $0.32 mm$ gap) may ensure that pressure and density gradients are primarily in the vertical direction. Reppy’s experiments also involve a particularly simple plastic deformation—pure vertical shear within the annular gap. Perhaps the deformation and annealing produce very little of the radial mass redistribution that would change the moment of inertia (and shift the overall torsional oscillator frequency), allowing the intrinsic behavior to be seen. This paper will certainly spur new torsional oscillator measurements to see how the effects it describes depend on details of cell design.

By plastically deforming helium within a torsional oscillator, Reppy has introduced a new tool to study the unusual properties of solid helium. If the behavior he sees proves to be universal, it could shift the focus of research to the unusual effects of defects on the elastic behavior of solid helium. We still don’t understand this quantum solid, but this paper poses a crucial question: are we dealing with supersolidity at low temperatures or some remarkable form of quantum plasticity that leads to extraordinary softening at high temperatures?

References

A. F. Andreev and I. M. Lifshitz, Sov. Phys. JETP 29, 1107 (1969); D. J. Thouless, Ann. Phys. 52, 403 (1969); G. V. Chester, Phys. Rev. A 2, 256 (1970); A. J. Leggett, Phys. Rev. Lett. 25, 1543 (1970)
E. Kim and M. H. W. Chan, Nature 427, 225 (2004)
E. Kim and M. H. W. Chan, Science 305, 1941 (2004)
E. L. Andronikashvili, Sov. Phys JETP 18, 424 (1948)
J. D. Reppy, Phys. Rev. Lett. 104, 255301 (2010)
J. T. West, O. Syshchenko, J. Beamish, and M. H. W. Chan, Nature Phys. 5, 598 (2009)
A. S. C. Rittner and J. D. Reppy, Phys. Rev. Lett. 97, 165301 (2006)
A. S. C. Rittner and J. D. Reppy, Phys. Rev. Lett. 98, 175302 (2007)
J. Day and J. Beamish, Nature 450, 853 (2007)
J. Day, O. Syshchenko, and J. Beamish, Phys. Rev. B 79, 214524 (2009)
A. C. Clark and M. H. W. Chan, Phys. Rev. B 77, 184513 (2008)
A. C. Clark, J. T. West, and M. H. W. Chan, Phys. Rev. Lett. 99, 135302 (2007)
M. H. W. Chan (private communication)
K. Shirahama (private communication)
H. Kojima (private communication)

About the Author

John Beamish began studying solid helium and dislocations as a graduate student at the University of Alberta, where he received his Ph.D. in 1982. His interest in quantum solids continued while he was a post-doctoral fellow at Brown University, a faculty member at the University of Delaware, and after he returned to the University of Alberta in 1991, where he is now a professor of physics. He also spent time as a visiting professor at the Pennsylvania State University and at Cornell University. In addition to supersolidity and quantum solids, his research interests include acoustics, freezing, and other phase transitions in confined liquids, superfluidity, and the low-temperature properties of aerogels and other porous glasses.