Keeping atoms synchronized for better timekeeping

Kurt Gibble

Viewpoint

Keeping atoms synchronized for better timekeeping

Kurt Gibble

Department of Physics, The Pennsylvania State University, University Park, PA 16802, USA

July 6, 2010• Physics 3, 55

In a new regime for atomic clocks, strong interactions between atoms dramatically increase the clock’s coherence time.

Figure caption — **Figure 1:** (a) Bloch sphere representation of two atomic coherences that are described by fictitious red and blue spins. The spins dephase by precessing in the horizontal plane with opposite dephasing torques $D$ . (b) Triplet and singlet energy eigenstates for two interacting spins. In this picture, dephasing is a precession between the triplet state $| t 〉$ and the singlet $| s 〉$ . The precession is inhibited when the spins interact strongly, $ω_{ex} ≫ D$ , shifting the energy of the singlet state. (c) The interactions exert a torque $ω_{ex}$ on the spins about their mean spin. When $ω_{ex} ≫ D$ , the precession of the spins about the vector sum of the two torques $ω_{ex}$ and $D$ , so they no longer precess about the equator, giving extraordinarily long coherence times for a clock.

Atomic clocks often have a limited coherence time due to the interactions between the constituent atoms. While it is usually very easy to use fewer atoms to reduce the interactions, this leads to lower signal-to-noise and less precise measurements. This tension between strong interactions and noise seems unavoidable and limits the accuracy of the world’s best cesium clocks, the keepers of international atomic time [1,2]. As reported in a paper in Physical Review Letters, Christian Deutsch and coworkers at three laboratories in Paris, France, have circumvented this seemingly unavoidable compromise by showing that a clock’s coherence can actually be enhanced by strong atomic interactions [3]. Even better, strong atomic interactions might also reduce the clock’s systematic frequency shifts. The authors demonstrated long coherence times with an “atom chip,” but their key requirements can also be satisfied in optical lattice clocks [4].

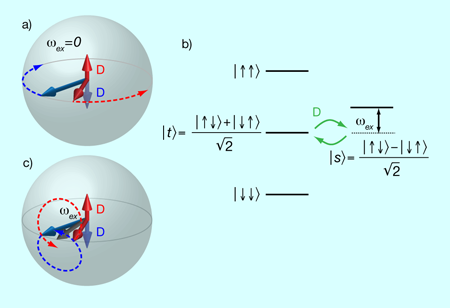
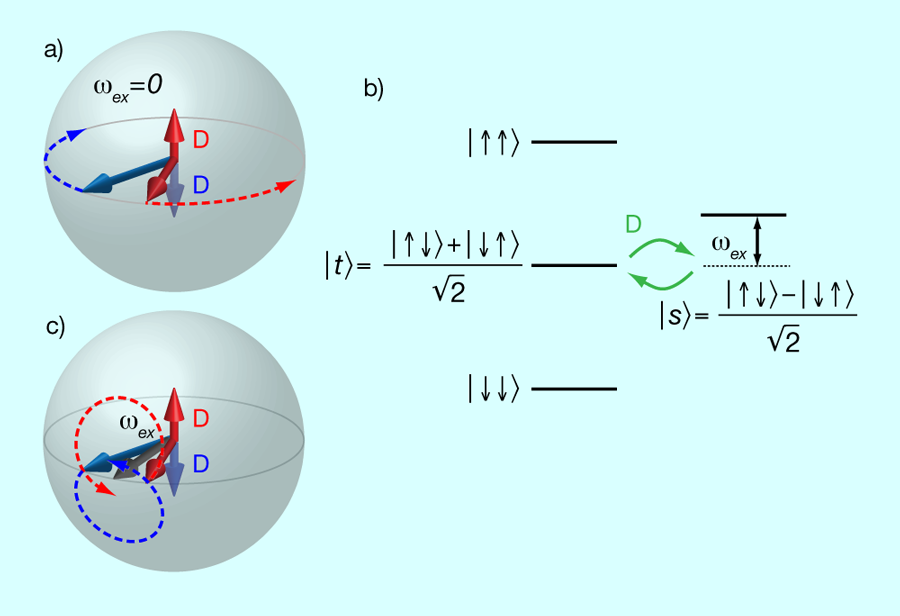
The tick rate or frequency $ν$ of an atomic clock is given by the energy difference between two atomic eigenstates, $ν = Δ E / h$ . Clocks based on trapped atoms can suffer from a lack of coherence if the trap strength is different for the two atomic eigenstates. The tick rate of atoms in higher energy trap states can be faster than for those in lower energy trap states, limiting the coherence time. Researchers in this field often represent the coherence of a system of two-level atoms with a geometric tool called the Bloch sphere: vectors pointing to the north and south poles represent the pure states $| ↑ 〉$ and $| ↓ 〉$ , while vectors on the equator represent equal superpositions of $| ↑ 〉$ and $| ↓ 〉$ . In Fig. 1(a), the dephasing of the atomic coherences is depicted as the red and blue arrows precessing in opposite directions on the equator of the Bloch sphere. Dephasing is a torque $D$ acting in opposite directions on the fictitious spin vectors that represent the superposition of the two atomic eigenstates. The dephasing broadens the linewidth of the clock and often degrades the clock’s stability. Although there are techniques for some clocks that make the trap strengths nearly equal for the two eigenstates, such as magic wavelengths for optical lattice clocks [4], other effects, including atomic interactions, also limit the maximum coherence time. Even when traps are delicately tuned [5], the coherence times are still limited, as this tuning is not very robust.

The essential trick of Deutsch et al. is to increase the atomic interactions so that they are much greater than the dephasing rates in their trap. However, while the interactions have to be strong enough to overcome dephasing, they also have to be weak enough so that the atoms do not rapidly scatter between different trap states. This is the Knudsen gas regime, accessible at low energies where the de Broglie wavelength is much longer than the atomic scattering length. A second essential feature is to use fermions, or “fermionic-like” atoms. The mechanism can already be seen when there are as few as two particles in the trap. The energy eigenstates of a two-particle system are shown in Fig. 1(b). At low temperatures, the Pauli principle ensures that identical fermions have no interactions, a desirable regime for making good clocks. In Fig. 1(b), there are no interactions for the three states with spin wave function that are symmetric under particle exchange—both fermions in the lower or upper states, or the symmetric combination of both spin states, $| t 〉$ . On the other hand, the antisymmetric spin combination, the pseudo spin singlet state $| s 〉$ , has a symmetric spatial wave function and therefore can have strong interactions at low temperature. Deutsch et al., in fact, use a boson, $^{87} Rb$ —it has the unique property that all three of the relevant scattering lengths, $a_{↑ ↑}$ , $a_{↓ ↓}$ , and $a_{↑ ↓}$ , are very nearly identical. This shifts all of the spin-symmetric triplet states by the same energy, but not the singlet state. Thus this special boson has the same energy spectrum as fermions [6,7].

In the singlet-triplet basis of Fig. 1(b), dephasing is a precession of the atoms between the singlet state $| s 〉$ and the triplet state $| t 〉$ . The different tick rates of the two atoms is precisely a different phase evolution of the two coherences, giving a precession from the triplet state $| t 〉$ to $| s 〉$ , back to $| t 〉$ , and so on. When strong interactions split the energy levels of singlet and triplet states by much more than the dephasing rate, the precession from $| t 〉$ to $| s 〉$ becomes energetically forbidden. In this way, Deutsch et al. robustly inhibit dephasing and observe long coherence times. Pairs of atoms do populate both the singlet and the triplet states, but the coupling $D$ between them becomes negligible for strong interactions $ω_{ex}$ . When the interactions are weak, the atoms rapidly dephase in $100 ms$ , but for strong interactions, the coherence decays negligibly in $5 s$ , suggesting coherence times as long as a minute!

Deutsch et al. analyze the precession of individual spins due to the interactions, whereas the basis set in Fig. 1(b) is comprised of the eigenstates of the atomic interactions [7]. Both basis sets offer insight. In Fig. 1(c), the individual spins precess about one another at a frequency given by the atomic interaction energy $ω_{ex}$ , and the dephasing is a torque in the $z$ direction, opposite for each spin. If the precession of each spin about the other is much larger than the dephasing rate, the smaller dephasing torque does not deflect the spin significantly throughout the cycle. They offer an analogy to rephasing in a spin-echo. For those familiar with detuned Rabi flopping, it is a mathematically exact analogy, as can be seen from Fig. 1(b). Rotating Fig. 1(c) so that $ω_{ex}$ points downward gives the usual Bloch sphere representation for detuned Rabi flopping. The Rabi frequency of the electromagnetic field $Ω$ is analogous to the dephasing torque $D$ , and the detuning for Rabi flopping is analogous to $ω_{ex}$ . The total torque on each spin is given by the vector sum of $ω_{ex}$ and $D$ for each spin. Thus, when $ω_{ex} ≫ D$ , the total torque is nearly along $ω_{ex}$ and the spins precess about it, never dephasing significantly.

In addition to long coherence times, Deutsch et al. also observe revivals of the coherence when the interactions are more moderate and allow some dephasing. At first, the transition contrast goes down as the spins precess for a fraction of a cycle because the light that excited the atoms no longer couples to them in the same way. But, waiting a little longer, the spins precess through one full cycle and are back to where they started. If a second pulse of light is applied at this time, the transition can be observed with a large contrast, giving the revival. Indeed, Deutsch et al. convincingly observe the oscillation of the contrast, seeing that the spin precession rate is proportional to the interactions. In the singlet-triplet basis, the revival occurs when the singlet state acquires phase factors $exp (- i ω_{ex} t)$ where the phase $ω_{ex} t$ is a multiple of $2 π$ . Subsequent revivals are smaller since they may be washed out by scattering to other trap states and also by the distribution of interaction strengths when the atoms populate many trap states.

This suppression of dephasing is fairly general. It should be directly applicable to optical lattice clocks. Rapid spin exchange for room-temperature atoms behaves similarly and has also yielded long coherence times, leading to more sensitive atomic magnetometers [8]. Further, recent work suggests that strong interactions might also eliminate the systematic clock error due to collisional frequency shifts [9]. Thus, with strong interactions, chip and lattice clocks might be able to have both long coherence times, giving higher stability, and potentially improved accuracy. However, an important future question is how can we establish the accuracy of a clock with strong interactions? Conventionally, the clock’s frequency is linearly proportional to the atomic density, allowing an extrapolation of the clock’s frequency to that of a single atom. But here, reducing the density will degrade the clock’s stability and its accuracy, so some new understanding or tricks may be needed to prove the accuracy of such a clock. Nonetheless, many important clock applications require only stability and not accuracy. Deutsch et al. have shown extraordinarily long coherence times with a robust mechanism that should be highly immune to small drifts of the clock’s parameters. They realize an important step towards miniature atomic chip clocks with high stability.

References

K. Gibble and S. Chu, Phys. Rev. Lett. 70, 1771 (1993)
See R. Wynands and S. Weyers, Metrologia 42, S64 (2005) and references therein
C. Deutsch, F. Ramirez-Martinez, C. Lacroûte, F. Reinhard, T. Schneider, J. N. Fuchs, F. Piéchon, F. Laloë, J. Reichel, and P. Rosenbusch, Phys. Rev. Lett. 105, 020401 (2010)
H. Katori et al., Phys. Rev. Lett. 91, 173005 (2003)
D. M. Harber, H. J. Lewandowski, J. M. McGuirk, and E. A. Cornell, Phys. Rev. A 66, 053616 (2002)
J. N. Fuchs, D. M. Gangardt, and F. Laloë, Phys. Rev. Lett. 88, 230404 (2002)
K. Gibble, Phys. Rev. Lett. 103, 113202 (2009)
W. Happer and H. Tang, Phys. Rev. Lett. 31, 273 (1973); M. P. Ledbetter and M. V. Romalis, 89, 287601 (2002)
M. D. Swallows, Michael Bishof, Yige Lin, Sebastian Blatt, Michael J. Martin, Ana Maria Rey, and Jun Ye, arXiv:1007.0059; A. M. Rey, A. V. Gorshkov, and C. Rubbo, Phys. Rev. Lett. 103, 260402 (2009); K. Gibble, Proc. 2010 IEEE Int. Freq. Control Symp. (to be published)

About the Author

Kurt Gibble is Professor of Physics at The Pennsylvania State University. After obtaining a Ph.D. from JILA at the University of Colorado, Boulder, he was a postdoc at Stanford University, and faculty at Yale University before moving to Penn State in 2001. His research addresses a range of topics on microwave, optical, and space-based atomic clocks, and the scattering of ultracold atoms. He is a fellow of the American Physical Society.