Suppressed fluctuations in Fermi gases

Christoph I. Westbrook

Viewpoint

Suppressed fluctuations in Fermi gases

Laboratoire Charles Fabry de l'Institut d'Optique, Centre National de la Recherche Scientifique, 91127 Palaiseau Cedex, France

July 19, 2010• Physics 3, 59

Sometimes experimental noise is actually signal. Two groups have shown how density fluctuations in a gas of identical fermions can be used as a nanokelvin thermometer.

Figure caption — **Figure 1:** A schematic illustration of the relationship between density, density fluctuations, and temperature in a one-dimensional Fermi gas. The three grids represent a 1D phase space, with axes $x$ and $p_{x}$ . Each box represents a phase-space cell (with volume = $h$ ). At most, one particle is permitted per box. The density corresponds to the number of atoms per column. The temperature is related to how the number of atoms per row decreases with $p_{x}$ . A higher temperature means more population in high momentum states. (a) A cold dense gas. (b) A cold but less dense gas. (c) A dense but hotter gas. The density fluctuations (that is, the variance in the number of particles per column) are lowest in (a). If the absolute density is known, a measurement of the density fluctuations gives information about the absolute temperature. This relationship is embodied in the fluctuation and dissipation theorem.

Suppose you have a large volume of an ordinary gas and you examined a small subvolume within it that contains a mean number of particles $N$ . You would expect that the variance of that number, $δ N^{2}$ , resulting from repeated measurements, is also equal to $N$ . By “ordinary,” I mean two things. First, the gas is ideal, i.e., composed of particles with negligible interactions, and second, the gas is “classical,” i.e., composed of distinguishable particles. We often refer to this behavior of the variance as shot noise. A common example of this noise is what we hear when rain drops hit a tin roof, although in that example, $N$ is the number of hits within a time interval, rather than particles within a sub-volume.

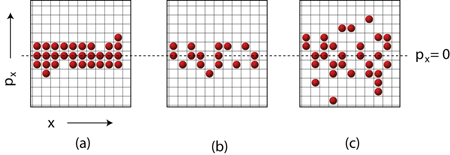
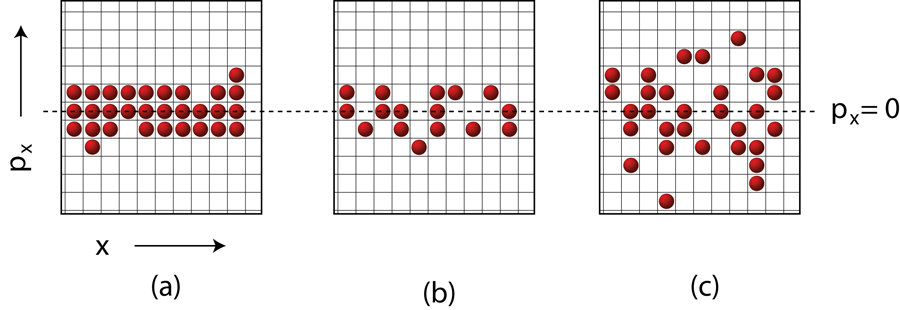
But if the particles are quantum mechanically identical (that is, are subject to quantum mechanical exchange symmetry), the above expectation is incorrect. Ensembles of identical particles can be either bosons or fermions and their fluctuation properties are very different. Most statistical physics textbooks show that $δ N^{2} = N \pm N^{2} / Z$ , where $Z$ is the number of elementary phase-space cells occupied by the small volume $Z =$ $Δ$ $x$ $Δ$ $y$ $Δ$ $z$ $Δ$ $p_{x}$ $Δ$ $p_{y}$ $Δ$ $p_{z} / h^{3}$ , where $h$ is Planck’s constant, and the plus and minus signs refer to bosons and fermions, respectively [1]. This formula, at least for the case of bosons, was already demonstrated by Einstein in 1925 in one of his famous papers on the theory of the ideal quantum gas [2]. Thus the number of particles in a small subvolume of a gas will exhibit fluctuations either above or below shot noise, depending on whether it is composed of bosons or fermions (Fig. 1). Now, two groups, one at the Eidgenössische Technische Hochschule (ETH) in Zurich, Switzerland [3], and the other at the Massachusetts Institute of Technology [4] in the US have beautifully demonstrated the statistical properties of fermions by measuring the fluctuations in ultracold atomic gases.

Most of us heard about this difference in statistical behavior of bosons and fermions as students. But many of us have forgotten it, partly because the phenomenon is difficult to observe directly. The reason is that in most circumstances, the number of phase-space cells involved is very large. This suppresses the $N^{2}$ term and makes the variance look very close to that of a classical gas. In order to observe such fluctuations in space, it is important to have a very low temperature since that will reduce the size of $Δ$ $p_{x}$ $Δ$ $p_{y} Δ$ $p_{z}$ . It is also favorable to have a high density because that means that for the subvolume in question, $N$ will be large and the $N^{2}$ term will make itself felt. High density and low temperature mean approaching quantum degeneracy—a high occupation of the individual phase-space cells. For fermions, the highest occupation is unity, and indeed, in a Fermi gas at zero temperature, the number variance vanishes. The idea is illustrated in Fig. 1.

The work of Torben Müller and colleagues at ETH [3] and Christian Sanner and colleagues at MIT [4] has come close to this ideal, using trapped degenerate Fermi gases. Thus they have given us a striking illustration of the fluctuation properties of ideal quantum gases. Both experiments use optically trapped $^{6} Li$ atoms. After cooling the cloud to degeneracy, the researchers capture an image of the atomic clouds on CCD cameras, using resonant light. The observation volume corresponds to the resolution of the imaging system and the thickness of the cloud along the imaging beam propagation direction. The number of atoms in this volume is related to the amount of light detected in the corresponding optical resolution element. To obtain the variance, the measurement is repeated many times. The experiment is delicate in part because corrections must be made for other fluctuating quantities, particularly those due to the photon shot noise—the same number of atoms does not always scatter the same number of photons during a given exposure. It is also desirable to absolutely calibrate the number of atoms, as will be shown in the next paragraph. Both papers show the atomic density as a function of position and of its variance. (The density varies with position because the clouds are trapped in approximately harmonic potentials.) For degenerate clouds, the densest parts of the clouds show a decidedly smaller relative variance $δ$ $N^{2} / N$ than the less dense ones. For nondegenerate clouds the relative variance remains close to unity.

In a slightly more sophisticated interpretation of the data, one can invoke the fluctuation dissipation theorem, which relates the fluctuations of a given quantity to the temperature and the corresponding susceptibility [5]. The appropriate susceptibility for the density is the isothermal compressibility. For an ideal Fermi gas, the compressibility is known, and thus density fluctuation measurements amount to temperature measurements. Absolute fluctuation measurements give absolute temperatures. This fact may prove extremely useful in the future because measuring the temperature of a degenerate gas can be difficult. For example, the momentum profile of a Fermi gas becomes nearly independent of temperature when the gas is highly degenerate. Fluctuations in a degenerate Fermi gas, however, decrease linearly with temperature.

As can be seen in the list of references of the two papers, other examples of exploring fluctuation properties of low-temperature gases exist—mostly for Bose gases. Most of these experiments also involved ideal or weakly interacting gases. An important issue in this field is the understanding of strongly interacting systems, such as Mott insulators, Tonks Girardeau gases (dilute 1D Bose gases in which interactions cause strong anticorrelations), paired superfluids (such as the BCS superconductor phase), and other quantum correlated phases. The study of fluctuations in these systems is just beginning, and promises to lead to new insights. As we begin to understand these more complex phenomena, fluctuation measurements could very well end up as the thermometer of choice for further studies.

References

L. Landau and E. Lifschitz Statistical Physics, Part 1 (Pergamon, Oxford, 1980)[Amazon][WorldCat]
A. Einstein, Sitz. Ber. Preuss. Akad. Wiss. 3 (1925)
T. Müller, B. Zimmermann, J. Meineke, J-P. Brantut, T. Esslinger, and H. Moritz, Phys. Rev. Lett. 105, 040401 (2010)
C. Sanner, E. J. Su, A. Keshet, R. Gommers, Y-i. Shin, W. Huang, and W. Ketterle, Phys. Rev. Lett. 105, 040402 (2010)
K. Huang, Introduction to Statistical Physics (Taylor and Francis, London, 2001)[Amazon][WorldCat]

About the Author

Chris Westbrook earned a Ph.D. in physics from the University of Michigan in 1987. He then spent five years at the National Institute of Standards and Technology in Gaithersburg, MD, before accepting a position with the French CNRS at the Laboratoire Charles Fabry de l’Institut d’Optique near Paris. His main research interests have been the development of laser cooling, the study of degenerate quantum gases, and atom optics.