Laminar, turbulent, or doubly turbulent?

Carlo F. Barenghi

Viewpoint

Laminar, turbulent, or doubly turbulent?

Carlo F. Barenghi

School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK

July 19, 2010• Physics 3, 60

Though often ignored, the normal component of a superfluid reveals much about turbulence in a two-fluid system.

Figure caption — **Figure 1:** Schematic of an experiment for observing counterflow between the normal and superfluid components of helium. (Left) At the closed end of the channel, a resistor (A) dissipates heat into the liquid helium. Heat is carried by the normal fluid with velocity $V_{N}$ toward the helium bath (B) at the other end of the channel. The superfluid flows with velocity $V_{S}$ toward the heater. If the heat flux is large enough, the superfluid becomes turbulent and forms a tangle of quantized vortex lines (C). Sharp tungsten needles (D) near the heater produce metastable helium molecules, which are transported by the normal fluid and detected by the probe laser (E) further down the channel. (Right) Fluorescent images of ${He}_{2}$ molecules at different times show that an initial line of molecules remains a line, proving that the normal fluid has a flat velocity profile (F) consistent with turbulent flow, rather than a laminar parabolic profile (G).

In a paper appearing in Physical Review Letters [1], Wei Guo, Sidney Cahn, James Nikkel, and Dan McKinsey at Yale University, US, and Joe Vinen at the University of Birmingham, UK, describe the new flow visualization technique they have developed to solve a decade-old puzzle of the two-fluid model of superfluid helium [2].

The two-fluid model was invented by Laszo Tisza and Lev Landau in the late 1930s to account for the remarkable flow properties of liquid helium when cooled below $2.17 K$ . These properties include the fluid’s ability to perfectly conduct heat and to flow without friction. This latter property, called superfluidity, is akin to superconductivity.

To describe the two-fluid model it is useful to recall Bose-Einstein condensation of an ideal gas of bosons. At a temperature $T$ below the critical temperature $T_{c}$ , the number $n_{0}$ of particles in the ground state, the condensate, is $n_{0} = n [1 - (T / T_{c})^{3 / 2}]$ , where $n = n_{0} + n'$ is the total number of particles and the $n'$ particles are in excited states. If $T$ is raised from absolute zero to $T_{c}$ , the ground-state fraction $n_{0} / n$ decreases from unity to zero. Since all ground-state particles are in the same state, the entropy of this fraction of the gas is zero. Entropy and other thermal properties of the system depend entirely on the particles in the excited states: let us call them the “normal fluid” fraction.

The interaction between particles slightly complicates things—liquid helium is not an ideal gas and an ideal gas is not a superfluid. But we can apply similar ideas to liquid helium below its critical temperature $T_{c} = 2.17 K$ , and model it as the mixture of two interpenetrating fluids: the superfluid component, which has zero viscosity, and the normal fluid component, which is viscous (like ordinary air or water). Since all helium atoms are the same—the normal fluid and superfluid components cannot be separated—this mixture of two fluids may seem more a mathematical model than a physical reality, but in practice, this model is a convenient way to describe what we see experimentally.

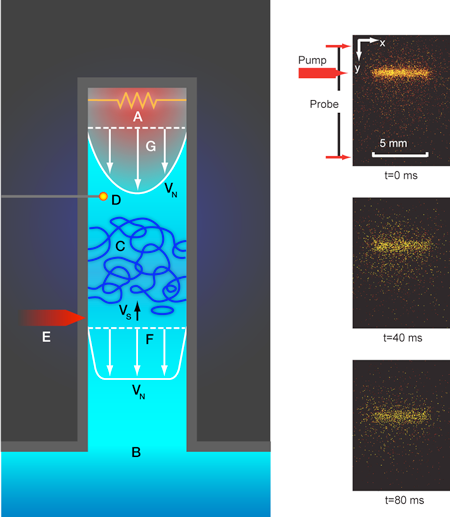
In particular, the two-fluid model predicts exactly what happens if heat is dissipated into the liquid helium by an electrical resistor (see Fig. 1, left): zero-entropy superfluid flows toward the heater, where it is converted into an entropy-carrying normal fluid that then flows away from the heater. In this way, a relative velocity difference (or counterflow) between the two fluids occurs that is proportional to the applied heat flux.

Counterflow is a mechanism of heat conduction in which the relative motion of two fluids prevents the formation of any hot spot and explains why bubbles don’t form in boiling liquid helium below $T_{c}$ . This (apparently) ideal heat transfer makes liquid helium very useful to engineers: lacking any other usable fluid (below $4 K$ , all other materials would be frozen), liquid helium can cool devices of any kind, from infrared detectors on board orbiting satellites, to the powerful superconducting magnets that accelerate elementary particles or that form the heart of medical imaging equipment.

There is, however, a limit to the ability of counterflow to perfectly iron out thermal differences—a fact that Joe Vinen discovered 50 years ago [3]. If the applied heat flux exceeds a critical value, the smooth flow of the superfluid breaks down into a disordered tangle of quantized vortex filaments, which induce thermal gradients and dissipate kinetic energy. The turbulence of the superfluid component, called quantum turbulence, consists of tiny quantized tornadoes, and is currently studied not only in liquid helium ( $^{4} He$ ) [4] but also in other quantum fluids, including $^{3} He$ [5] and, since last year, in atomic Bose-Einstein condensates [6].

Quantum turbulence is an exciting research area. There are, for example, intriguing similarities between quantum and ordinary turbulence, such as the fact that they have the same (Kolmogorov) energy spectrum [7]. But there are subtle differences too, such as the fact that the velocity statistics of quantum turbulence follow a power-law distribution, rather than the Gaussian distribution found in ordinary turbulence [8].

Overshadowed by its quantum fluid partner, the normal fluid component has, in some sense, been forgotten. With their recent work, Guo et al. [1] have just put the normal component back on center stage. They started with what is known about the velocity profile of viscous fluids like water. When these fluids flow slowly along a channel, the profile is parabolic (Poiseuille flow): the maximum speed at the apex of the parabola occurs at the channel’s center, while viscous forces slow down the water and bring it to rest near the walls. If the flow if fast enough, this parabolic laminar profile becomes unstable and breaks up into a jumbled mess of turbulent time-dependent eddies. A time-average of the turbulent velocity of such a liquid reveals a profile that is flat across the channel, with the exception of thin boundary layers near the walls where the velocity becomes zero.

The natural question is the following: What happens if the water is replaced by liquid helium, which contains viscous and nonviscous components? Shouldn’t we expect the normal fluid, which is also viscous, to behave in the same way? Until Guo et al.’s experiment, nobody knew the answer for sure, because, although the concept of a normal fluid was invented seventy years ago, nobody had seen it until very recently.

This perhaps surprising lack of progress is a result of how difficult it is to visualize flow at temperatures near absolute zero. Fluid dynamicists know many tricks to make turbulence visible: ink, smoke, reflective “Kalliroscope” flakes, hydrogen bubbles, hot wire and laser Doppler wind-speed detection (anemometry), particle image velocimetry, particle tracking, pH indicators, etc. In contrast, low-temperature physicists have had a paltry supply of techniques, and those few that were available could only measure quantities averaged over a large region, often missing the details of fluctuations and flow patterns.

A few years ago, recognizing this problem, researchers at the Universities of Florida and Maryland developed particle imaging and tracking methods based on micron-sized polymer spheres [9] and solid hydrogen particles [10], respectively. With these techniques, it was confirmed, for example, that during heat transfer, normal fluid and quantized vortices move in opposite directions [10].

The tendency of micron-sized tracers to become trapped in quantized vortices, however, greatly complicates the interpretation of the results [11], so Dan McKinsey’s group at Yale developed a radically new method. They applied a large negative voltage to sharp tungsten needles in a helium counterflow channel to create helium molecules ( ${He}_{2}$ ) in the metastable triplet state with a typical decay time of about $13 s$ . They were then able to image the molecules with cyclic laser induced fluorescence. Since the ${He}_{2}$ molecules are only $1 nm$ , they are much smaller than tracer particles and do not fall into quantizes vortices. Rather, they behave as free impurities, tracing the motion of the normal fluid.

In their new experiments, the Guo et al. optically excited a line of helium molecules across the channel and imaged these “tagged” molecules as they drifted with the normal fluid away from the heater. They observed the expected relation between the heat flux and the average normal fluid velocity. For large heat flux, the initially straight line of molecules remained straight, indicating a flat normal fluid velocity profile across the channel. This would be consistent with either a laminar profile flattened by the mutual friction force between the excited states and the quantized vortices, or with a turbulent normal fluid scenario that was predicted years ago by David Melotte and me [12]. The observed broadening of the line of molecules with increasing time, too rapid to be explained by diffusion, suggests that the normal fluid is turbulent.

In a second control experiment, the group tagged and imaged a cluster of molecules in the middle of the channel with the heater low enough that both normal fluid and superfluid were expected to be laminar. While this did not permit them to image the velocity profile as they did with the first experiment, they did observe that the drift velocity of this cluster was consistent with the speed one would expect if the cluster were moving at the apex of the laminar parabolic profile.

Guo et al.’s results demonstrate that, in the turbulent heat transfer of liquid helium, the normal fluid can undergo a transition and become turbulent alongside the turbulent superfluid. What are the prospects of this experiment? Turbulence is still a major challenge of classical physics, and many practical applications (from jet engines to weather forecast) require better control or mastering of it. Questions that drive this field include: Is ordinary turbulence the classical limit of quantum turbulence? Can the complexity of eddies and swirls in a turbulent stream be better understood in terms of the dynamics of a large number of discrete vortex filaments, each carrying one unit of circulation? In the last few years there has been much progress in interpreting quantum turbulence experiments in terms of classical turbulence theory [13], using tools and ideas such as Reynolds number [14], Kolmogorov energy spectra [7], velocity statistics [8], cascades [15,16], and fractals [16]. The beauty of physics is its unity: one feels almost a sense of awe when a concept that used to be limited to one discipline (in this case fluid dynamics) suddenly becomes relevant to other areas (atomic physics and condensed matter physics). In this spirit, Guo et al.’s experiment provides both a new experimental tool to study turbulence and raises a theoretical challenge for understanding a double-turbulent system!

References

W. Guo, S. B. Cahn, J. A. Nikkel, W. F. Vinen, and D. N. McKinsey, Phys. Rev. Lett. 105, 045301 (2010)
R. J. Donnelly, Quantized Vortices in Helium II (Cambridge University Press, Cambridge, 1991)[Amazon][WorldCat]
W. F. Vinen, Proc. R. Soc. London A 240, 114 (1957)
P. M. Walmsley and A. I. Golov, Phys. Rev. Lett. 100, 245301 (2008); M. Blazkova, D. Schmoranzer, L. Skrbek, and W. F. Vinen, Phys. Rev. B 79, 054522 (2009); P.-E. Roche, P. Diribarne, T. Didelot, O. Francais, L. Rousseau, and H. Willaime, Europhys. Lett. 77, 66002 (2007)
D. I. Bradley, S. N. Fisher, A. M. Guenault, R. P. Haley, S. O’Sullivan, G. R. Pickett, and V. Tsepelin, Phys. Rev. Lett. 101, 065302 (2008); V. B. Eltsov, A. I. Golov, R. de Graaf, R. Hanninen, M. Krusius, V. S. L’vov, and R. E. Solntsev, 99, 265301 (2007)
E. A. L. Henn, J. A. Seman, G. Roati, K. M. F. Magalhaes, and V. S. Bagnato, Phys. Rev. Lett. 103, 045301 (2009)
J. Maurer and P. Tabeling, Europhys. Lett. 43, 29 (1998)
A. C. White, C. F. Barenghi, N. P. Proukakis, A. J. Youd, and D. H. Wacks, Phys. Rev. Lett. 104, 075301 (2010); M. S. Paoletti, M. E. Fisher, K. R. Sreenivasan, and D. P. Lathrop, 101, 154501 (2008)
T. Zhang and S.W. Van Sciver, Nature Phys. 1, 36 (2005)
G. P. Bewley, D. P. Lathrop, and K. R. Sreenivasan, Nature 441, 588 (2006)
Y. A. Sergeev, C. F. Barenghi, and D. Kivotides, Phys. Rev. B 74, 184506 (2006)
D. J. Melotte and C. F. Barenghi, Phys. Rev. Lett. 80, 4181 (1998)
W. F. Vinen and J. J. Niemela, J. Low Temp. Phys. 128, 167 (2002)
C. F. Barenghi, Physica D 237, 2195 (2008)
E. Kozik and B. Svistunov, J. Low Temp. Phys. 156, 215 (2009); V. S. L’vov and S.V. Nazarenko, arXiv:0911.2065 (2010)
A.W. Baggaley and C. F. Barenghi, arXiv:1006.2934 (2010)

About the Author

Carlo F. Barenghi obtained a doctorate in theoretical physics at the University of Milan in Italy and a Ph.D. in experimental physics at the University of Oregon at Eugene, US. He is currently professor of applied mathematics at Newcastle University, in the United Kingdom. His main interest is vortices in quantum fluids (superfluid helium and Bose-Einstein condensates). He is also keen on vortices and turbulence in ordinary fluids, including astrophysical fluids. Carlo Barenghi is a Fellow of the American Physical Society and a Fellow of the Institute of Physics.