Berry’s phase and quantization in topological insulators

M. Zahid Hasan

Viewpoint

Berry’s phase and quantization in topological insulators

Joseph Henry Laboratories, Department of Physics, Princeton University, Princeton, NJ 08544, USA

July 26, 2010• Physics 3, 62

The exactly quantized magneto-optical response of a topological insulator is a direct result of the Berry phase protected states on its surface.

Figure caption — **Figure 1:** The energy vs momentum of the states on the surface of a 3D topological insulator forms a Dirac cone. The red curve is a slice through this cone, measured with photoemission from the surface of the topological insulator ${Bi}_{2} {Se}_{3}$ . (Inset) Schematic of the full Dirac cone and the circulation of the spin states (yellow arrows) associated with each momentum state. The spin circulation pattern leads to a Berry’s phase of $π$ .

The most well-known example of a topological phase is a 2D electron gas at low temperatures and in a high-magnetic field, which has a quantized Hall conductance. However, the conducting states on the surface of a 3D topological insulator, while bearing some similarities to those in the 2D case, are a new state of matter [11–17]. Theorists are therefore keen to describe the exotic physical properties of 3D topological insulators, which should exhibit new quantization rules, and predict the ways in which they can be observed in experiments.

The distinction between topological insulators and conventional band insulators is evident in the space that contains their allowed wave functions, i.e., the Hilbert space. In some sense, topological insulators are defined by the fact that their Hilbert space topology cannot be easily perturbed to destroy the wave functions on the surface. Hence the surface electron modes are protected.

In the simplest description, the surface electron modes of a topological insulator are arranged in a single Dirac cone—the linear dispersion that describes massless particles—with a vortexlike spin arrangement (Fig.1). The circulating structure of the spins contributes a Berry’s phase of $π$ to the electronic (or hole) wave function [3–6] (recall that a spin- $1 / 2$ particle must undergo two complete rotations to acquire a phase of $2 π$ ). The Berry’s phase protects these surface states against backscattering from disorder and impurities and dictates new topological quantization rules [15,16].

The spin vortexlike pattern on the surface of a topological insulator exists in the presence of time reversal symmetry, but when this symmetry is broken—say, due to the presence of a magnetic field—a gap will open in the Dirac spectrum that disrupts the spin-texture. This can lead to unusual electromagnetic and magnetotransport effects in a topological insulator.

These effects can be quite spectacular when a magnetic field is applied perpendicular to the surface of a topological insulator. A magnetic field will induce Landau levels—the quantized states that give rise to the quantum Hall effect—to appear in the surface’s electronic spectrum. The Landau levels for Dirac electrons are special, however, because a Landau level is guaranteed to exist at exactly zero energy. Since the Hall conductivity $σ_{x y}$ increases by a conductivity quantum of $e^{2} / h$ when the Fermi energy crosses a Landau level, the presence of a Landau level at zero energy means the conductivity must be half-integer quantized: $σ_{x y} = (n + 1 / 2) e^{2} / h$ .

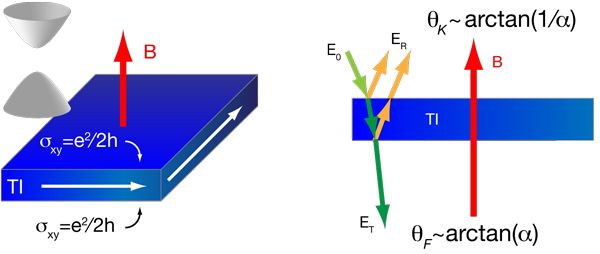
This behavior has been famously demonstrated in experiments on graphene, except that the Dirac points in graphene have a fourfold spin and valley degeneracy, which means the observed Hall conductivity is still integer quantized. At the surface of a bulk topological insulator, however, there is only a single spin-polarized Dirac cone (i.e., one that circulates in a particular direction) that carries $π$ Berry’s phase (Fig. 1). This “fractional” integer quantized Hall state $[σ_{x y} = (1 / 2) e^{2} / h$ for $n = 0]$ on the surface should be a cause for concern because the integer quantized Hall effect is always associated with chiral edge states (as opposed to helical surface states) and can only be integer quantized. The resolution is the mathematical fact that a surface cannot have a boundary. If the topological insulator is shaped like a slab (Fig. 2), the top surface and bottom surface are necessarily connected to each other, and will always be measured in parallel in transport, doubling the $1 / 2$ . The top and bottom can share a single chiral edge state, which carries the integer quantized Hall current.

A similar surface quantum Hall effect, known as the anomalous quantum Hall effect, can be induced with the proximity to a magnetic insulator. A magnetic field—say, from a nearby thin magnetic film—on the surface of a topological insulator lifts the spin degeneracy at the surface Dirac point. If the Fermi energy is in this induced energy gap, this leads to a half-integer quantized Hall conductivity $σ_{x y} = (1 / 2) e^{2} / h$ (Fig. 2) due to the Berry’s phase of $π$ on the topological surface.

To induce such a gap, Tse and MacDonald propose to place a thick film of a topological insulator between two ferromagnets. They then consider the electromagnetic response of a helical (spin-momentum locked) Dirac gas in a half-integer quantized Hall state. They showed that under such conditions, the polarization of light transmitted through a 3D topological insulator would always be rotated by a fixed angle of $arctan (α)$ : rotation by any arbitrary angle is not possible. The flipside of this transmission or “Faraday effect” is a quantized “Kerr effect,” where light reflected from the surface has its polarization rotated by a fixed amount of $arctan (1 / α)$ . The only requirement is that the light be at a frequency lower than the topological insulator band gap and the induced magnetic gap on the Dirac states.

This unusual optical response of 3D topological insulators comes from a combination of cavity confinement and the Hall conductivity of spin-helical Dirac modes on the surface: The incident light can only induce quantized currents with a certain spin helicity, which in turn affects the reflected and transmitted light. The fine structure constant $α$ dictates the coupling between the quantized currents and the electromagnetic wave. The Kerr rotation of $arctan (1 / α) \sim arctan (137) \sim π / 2$ suggests that polarization of the reflected light should exhibit a striking full-quarter rotation relative to the incident polarization direction of the light beam (Fig. 2).

The effect Tse and MacDonald predict is effectively insensitive to the precise value of the gap as long as it is finite, since one can always choose a lower frequency of the incident light. Working with far infrared light, these conditions are adequately met in the topological insulator ${Bi}_{2} {Se}_{3}$ [4,5]. This highly tunable material features almost ideal Dirac quasiparticle helical spin modes that are locked in by the Berry’s phase of $π$ , as in Fig. 1. The surface modes are well protected within a large band gap ( $\sim 0.3 eV$ ). To measure the magneto-optical effects directly, a film of ${Bi}_{2} {Se}_{3}$ would have to be thick enough that the surface electrons do not tunnel between the top and bottom surfaces, but films of this thickness could, in principle, be grown using molecular beam epitaxy.

Tse and MacDonald’s proposal for measuring topological quantization in units of the vacuum fine structure constant $α = e^{2} / ħ c$ could lead to a new metrological standard for fundamental physical constants [13–17]. In addition, observing topological quantization in ${Bi}_{2} {Se}_{3}$ would be confirmation, independent of spin-resolved photoemission, that topological order can exist in “ordinary” bulk solids. In the long run, classifying bulk solids in terms of topological quantization may turn out to be a more powerful method of identifying phases of matter beyond the standard Landau paradigm, which is based on the idea of spontaneously broken symmetry. Perhaps the most significant “effect” is that which the discovery of topological insulator states has had on research itself: physicists can now study the interplay of “topological order” and “broken-symmetry order” in real experiments and with real materials that are, in principle, accessible to anyone [12].

References

W-K. Tse and A. H. MacDonald, Phys. Rev. Lett. 105, 057401 (2010)
D. Hsieh, Y. Xia, L. Wray, Y. Hor, D. Qian, R. J. Cava, and M. Z. Hasan, Nature 452, 970 (2008)
For the Berry’s phase sensitive measurements, see, D. Hsieh, et al., Science 323, 919 (2009)
Y. Xia et al., Nature Phys. 5, 398 (2009); arXiv:0812.2078v1 (2008)
D. Hsieh et al., Nature 460, 1101 (2009)
P. Roushan et al., Nature 460, 1106 (2009)
A. Nishide et al., arXiv:0902.2251 (2009)
D. Hsieh et al., Phys. Rev. Lett. 103, 146401 (2009)
Y. L. Chen et al., Science 325, 178 (2009)
H. Lin et al., Phys. Rev. Lett. 105, 036404 (2010)
J. E. Moore, Nature 464, 194 (2010)
M. Z. Hasan and C. L. Kane, arXiv:1002.3895 (2010); Rev. Mod. Phys. (to be published)
X.-L. Qi and S.-C. Zhang, Phys. Today 63, No. 1, 33 (2010)
L. Fu and C.L. Kane, Phys. Rev. B 76, 045302 (2007)
X.-L. Qi, T. Hughes, and S.-C. Zhang, Phys. Rev. B 78, 195424 (2008)
A. Essin, J. E. Moore, and D. Vanderbilt, Phys. Rev. Lett. 102, 146805 (2009)
C. Day, Phys. Today 62, No. 4, 12 (2009)

About the Author

M. Zahid Hasan is an Associate Professor of Physics at Princeton University. He obtained his Ph.D. in 2002 from Stanford University, working at SLAC and Brookhaven National Laboratory. He was then a Robert H. Dicke Fellow in fundamental physics at Princeton and held several extended visiting appointments at Bell Laboratories (Murray Hill) and Lawrence Berkeley National Laboratory before joining the Faculty at Princeton. His research has focused on quantum Hall-like topological phases, exotic correlated superconductors, quantum phase transitions, and topological quantum computing physics. In recent years, he, along with his team, has experimentally discovered topological-order in bulk solids (3D topological insulators) including the single-Dirac-cone series using spin-resolved and phase-sensitive spectroscopic measurements.