Quantized topological surface states promise a quantum Hall state in topological insulators

Jacob W. Linder

Viewpoint

Quantized topological surface states promise a quantum Hall state in topological insulators

Department of Physics, Norwegian University of Science and Technology, N-7491 Trondheim, Norway

August 9, 2010• Physics 3, 66

The first experimental observation of Landau levels in the surface states of a three-dimensional topological insulator confirms the levels obey unconventional quantization rules.

Figure caption — **Figure 1:** (a) Illustration of the conventional integer quantum Hall effect found, e.g., in 2D semiconductor systems. (b) Illustration of the unconventional half-integer quantum Hall effect found, e.g., in a graphene layer. (c) The experimentally observed Landau quantization of the topological surface states in ${Bi}_{2} {Se}_{3}$ for several magnetic field strengths. Curves are offset vertically for clarity. Note in particular the peak occurring at the Fermi level (around $- 200 mV$ sample bias), which is independent of the field strength. This serves as a hallmark of the unconventional quantization form shown in (b). (d) STM picture of a ${Bi}_{2} {Se}_{3}$ surface in the presence of triangular-shaped defects (bright white spots). By selecting one point in such a map and plotting the $d I / d V$ curves as a function of bias voltage, one is able to probe the density of states similarly to (c).

The prediction [1] and experimental discovery [2,3] of a class of materials known as topological insulators is a major recent event in the condensed matter physics community. Why do two- and three-dimensional topological insulators (such as $HgTe / CdTe$ [2] and ${Bi}_{2} {Se}_{3}$ [3], respectively) attract so much interest? Thinking practically, these materials open a rich vista of possible applications and devices based on the unique interplay between spin and charge. More fundamentally, there is much to enjoy from a physics point of view, including the aesthetic spin-resolved Fermi surface topology [3], the possibility of hosting Majorana fermions (a fermion that is its own antiparticle) in a solid-state system [4], and the intrinsic quantum spin Hall effect, which can be thought of as two copies of the quantum Hall effect for spin-up and spin-down electrons [5]. Now, an exciting new addition to the above list comes from two teams that are reporting the first experimental observation of quantized topological surface states forming Landau levels in the presence of a magnetic field. The two papers - one appearing in Physical Review Letters by Peng Cheng and colleagues at Tsinghua University in China, and collaborators in the US, the other, appearing as a Rapid Communication in Physical Review B, by Tetsuo Hanaguri at Japan’s RIKEN Advanced Science Institute in Wako and scientists at the Tokyo Institute of Technology - pave the way for seeing a quantum Hall effect in topological insulators.

An ideal topological insulator is electrically insulating in its bulk, but has conducting electronic states that are formed on its surface (or edges in a two-dimensional material). These electronic states reside on a massless Dirac cone, a relativistic energy-momentum dispersion in reciprocal space. Dirac cones also appear in graphene, but there are essential differences between topological insulators and graphene. In a topological insulator, as opposed to the case for graphene, the surface states display a remarkable robustness against any type of disorder or perturbation that is invariant under time-reversal symmetry, even though the surface states in both of these systems are Dirac fermions. The reason for this is the seemingly trivial fact that the Brillouin zone in topological insulators features a single Dirac cone, thus an odd number, whereas in graphene the number of Dirac cones is even. This can be probed experimentally, e.g., via photoemission spectroscopy [3] to reveal how many Dirac cones exist in the Brillouin zone. In an environment with a single Dirac cone, Kramers’ theorem of degeneracy guarantees that the energy bands of the surface states in topological insulators must cross at the time-reversal invariant $Γ$ point at $k = 0$ . As a result, no disorder or perturbation that respects this time-reversal invariance can induce a gap in the surface-state spectrum.

Let us extend this reasoning to a three-dimensional topological insulator, in which the surface can be thought of as a two-dimensional metal, with carriers that will feature different spins depending on their direction of propagation. In such a two-dimensional electron system, the much-celebrated phenomenon known as the quantum Hall effect (QHE) is known to occur under appropriate circumstances. The QHE [8] was originally discovered in the context of two-dimensional electron gases at low temperatures, and under the application of a strong magnetic field perpendicular to the sample. In such a scenario, quantized orbits of motion are formed and the electrons in the sample can only occupy energy states belonging to quantized energy eigenvalues. More recently, the QHE was experimentally demonstrated to occur in graphene [9], but with a twist compared to the two-dimensional electron gas case. The special properties of the Dirac fermions in graphene cause the quantized conductance to form its characteristic plateaus at half-integer values of $e^{2} / h$ [10], in contrast to the integer values of $e^{2} / h$ observed in conventional two-dimensional electron gases. To understand this, it is instructive to consider the analytical expression for the Landau energy levels for the linear dispersion,

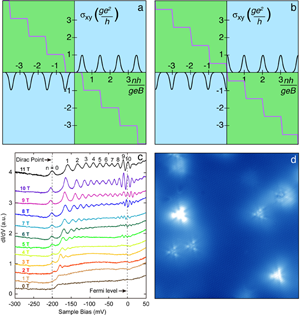
Here, $E_{F}$ is the Fermi level, $n$ is an integer, $v_{F}$ is the Fermi velocity, $e$ is the unit electric charge, $B$ is the field strength, and $ħ$ is Planck’s reduced constant. The most remarkable aspect of the above equation is the fact that there exists a Landau level that is completely independent of the magnetic field strength, namely, at $n = 0$ , $E_{0} = E_{F}$ . Compare this with the case of a conventional two-dimensional electron gas system with a parabolic dispersion (nonzero mass of the charge carriers), where such a zeroth Landau level is not permitted. How, then, is this related to the half-integer quantum Hall effect? The key observation here is that the conductance plateaus, serving as the hallmark of the QHE, occur whenever the chemical potential falls between two Landau levels. For a conventional QHE system, there is no zeroth Landau level, and thus a plateau appears at $σ_{x y} = 0$ . In contrast, if a zeroth Landau level exists, a plateau should exist right before and right after the Fermi level. When particle-hole symmetry holds in the system, the conductance is an odd function of energy, measured relative to the Fermi level. It therefore follows that the first conductance quantization plateaus must occur precisely at values $\pm (1 / 2) g_{s} e^{2} / h$ , thus being separated by $g_{s} e^{2} / h$ as they should. Both of the above scenarios are illustrated in Fig. 1(a) and (b).

Since the surface states in topological insulators are Dirac fermions, it follows from the above discussion that 3D topological insulators should feature such a unique zero-energy Landau level, just like graphene, and thus display the unconventional quantum Hall effect. But do they? The papers by Cheng et al. [6] and Hanaguri et al. [7] answer this question in the affirmative. Both research teams utilized a scanning tunneling microscopy/spectroscopy (STM/STS) technique to probe the current-voltage characteristics on the surface of high-quality ${Bi}_{2} {Se}_{3}$ samples. The STM provides information about the density of states of the surface electrons, as shown in Fig. 1(d), where the density of states and the triangular defects in ${Bi}_{2} {Se}_{3}$ are shown.

In their work, Cheng et al. [6] demonstrate an indisputable signature of Landau levels forming at the surface of the topological insulator ${Bi}_{2} {Se}_{3}$ under the influence of a strong external magnetic field, namely, a well-defined series of peaks in the conductance spectrum as a function of the bias between the STM/STS tip and the surface of the sample [see Fig. 1(c)]. Most interestingly, a peak is consistently observed right at the Fermi level and does not change with increasing field strength. This is precisely the famous zeroth Landau level. Cheng et al. then proceed to confirm further the two-dimensional nature of the Landau states in three-dimensional topological insulators by adding impurity silver atoms directly on the ${Bi}_{2} {Se}_{3}$ surface by means of evaporation. With increasing concentration of impurities, the Dirac point shifts in energy due to the electron transfer between silver atoms and the substrate and, more importantly, the Landau quantization eventually disappears. This does not mean that the surface states disappear, only the quantization.

Hanaguri et al. [7] also verify the presence of Landau levels using similar experimental techniques to those used in Ref. [6]. But in addition to this, they also develop of a clever strategy to probe explicitly the energy-momentum dispersion of the topological surface states. As quasiparticle interference modulations are absent in the Dirac cone on a topological insulator, due to the above-mentioned robustness of these states, this conventional tool for probing the $k$ -space structure of electronic states is rendered ineffective. Instead, Hanaguri et al. derive the $E$ − $k$ dispersion directly from the Landau-level spectroscopy by making use of the fact that the Landau orbits are quantized in $k$ space, and also employing a Bohr-Sommerfeld quantization condition which results in the formula $k_{n} = \sqrt{(2 e | n | B / ħ)}$ . In this way, a set of energy levels $E_{n}$ and belonging momenta $k_{n}$ can be obtained once $n$ and $B$ are specified, since $E_{n}$ scales with $\sqrt{| n | B}$ .

These experiments have established that the surfaces of topological insulators support Landau levels with an unconventional (half-integer) quantization. The next step to actually seeing the resulting quantum Hall effect will be transport measurements. However, important questions remain to be answered. For instance, what is the role of a possible Zeeman splitting with regard to these unconventional Landau levels? It is known that an out-of-plane exchange field will induce a mass gap in the surface-state spectrum of the topological insulators, thus destroying the surface states in a limited energy regime. If the Zeeman coupling to the external field is weak, an appreciable mass gap will only occur at high field strengths. But the profoundly different response of the topological surface states with respect to a Zeeman-field, because of the single Dirac cone compared to a conventional parabolic dispersion, suggests that more exciting effects than a mere spin-splitting of the Landau levels should occur. Such questions and more remain to be explored in this developing field of research, in addition to a direct experimental observation of the quantized conductance plateaus pertaining to the quantum Hall effect.

References

B. A. Bernevig, T. L. Hughes, and S.-C. Zhang, Science 314, 1757 (2006)
M. König et al., Science 318, 766 (2007)
D. Hsieh et al., Nature 452, 970 (2008); Y. Xia et al., Nature Phys. 5, 398 (2009)
N. Read and D. Green, Phys. Rev. B 61,10267 (2000); D. A. Ivanov, Phys. Rev. Lett. 86, 268 (2001); S. Das Sarma et al., Phys. Rev. B 73, 220502 (2006)
B. A. Bernevig and S.-C. Zhang, Phys. Rev. Lett. 96, 106802 (2006)
P. Cheng et al., Phys. Rev. Lett. 105, 076801 (2010)
T. Hanaguri, K. Igarashi, M. Kawamura, H. Takagi, and T. Sasagawa, Phys. Rev. B 82, 081305 (2010)
T. Ando, Y. Matsumoto, and Y. Uemura, J. Phys. Soc. Jpn 39, 279 (1975); K. Klitzing, G. Dorda, and M. Pepper, Phys. Rev. Lett. 45, 494 (1980)
Y. Zhang, Y.-W. Tan, H. L. Stormer, and P. Kim, Nature 438, 201 (2005)
V. P. Gusynin and S. G. Sharapov, Phys. Rev. Lett. 95, 146801 (2005)

About the Author

Jacob Linder obtained his Ph.D. in physics from the Norwegian University of Science and Technology (NTNU) in 2009. In 2010, he received awards from the Royal Norwegian Society of Sciences and Letters and from ExxonMobil for his work on quantum transport and proximity effects in unconventional superconducting hybrid systems. He is now an Associate Professor at NTNU, Norway. His research addresses a variety of topics related to proximity effects and quantum transport in hybrid structures, magnetization dynamics and spin-transfer torque, and properties of unconventional superconductivity.

Landau Quantization of Topological Surface States in ${Bi}_{2} {Se}_{3}$

Peng Cheng, Canli Song, Tong Zhang, Yanyi Zhang, Yilin Wang, Jin-Feng Jia, Jing Wang, Yayu Wang, Bang-Fen Zhu, Xi Chen, Xucun Ma, Ke He, Lili Wang, Xi Dai, Zhong Fang, Xincheng Xie, Xiao-Liang Qi, Chao-Xing Liu, Shou-Cheng Zhang, and Qi-Kun Xue

Phys. Rev. Lett. 105, 076801 (2010)

Published August 9, 2010

Read PDF