A new source of CP violation?
Scientific results are sometimes noteworthy because of the “wow” factor that captures the imagination: even David Letterman noticed the news that the expansion of the universe was accelerating. Other times, it may be the process of doing science that makes people take note: how sure are we that man-made global warming is really proven, given those stolen emails? Unfortunately, the process stories we encounter are too often sensationalist, as with the climate change example, and fail to illustrate how research is really conducted. While not without fits and starts, the real story of science is in the “how” that is behind the “wow.”
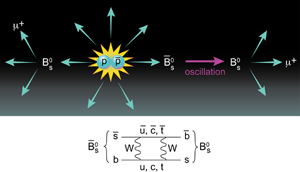
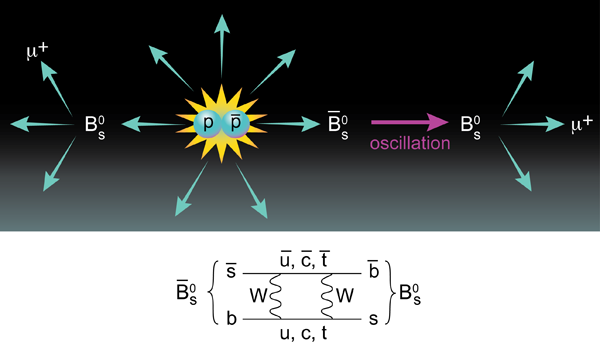
A recent high-energy physics result published in Physical Review Letters and Physical Review D from the D0 collaboration working at the Fermilab Tevatron accelerator may offer us a chance to watch both of these facets unfold together [1,2]. It may indeed be a “wow” discovery, heralding new physics, and is also a chance to watch the machinery of science confront a new result and vet it. The result in question? Abazov et al. report an unexpectedly large value of the same-sign dimuon charge asymmetry. This means that they see pairs of positive muons, μ+μ+, among the debris of their proton-antiproton collisions more often than they see pairs of negative muons, μ-μ- (Fig. 1). The key point is that their measurement violates CP symmetry, which relates the behavior of matter and antimatter particles.
CP violation is one of the three “Sakharov conditions” [3] required to explain the baryon asymmetry of the universe—that is, the puzzle of why there is so much matter and so little antimatter. While CP violation has been observed in several different ways since its surprising debut in 1964 [4], all current observations are consistent with a single root cause in the current standard model of particle physics. But detailed considerations lead experts to conclude that this known CP violation is not sufficient to explain the cosmic overabundance of matter. This is one of many reasons that high-energy physicists are pursuing signs of “new physics” beyond the standard model: what new source of CP violation is capable of producing the puzzling imbalance of matter that countenances our very existence?
CP violation was first observed in weak interactions of neutral kaons containing the strange quark. It was not until 2001 that a second system, the neutral B mesons, consisting of bottom quarks, also displayed this elusive effect [5,6]. The dimuon asymmetry reported by Abazov et al. is believed to also originate from these same B mesons. But it is not the mere presence of an effect, but the unexpectedly large size that caught their attention.
The type of CP violation relevant to the new D0 result involves oscillations of a B0s meson ( a ˉb quark bound to an s quark) into an anti- B0s meson ( b bound to ˉs), and also the analogous process with the B0d ( ˉbd) meson. That is, between the times of production and decay, the particle may transform into its antiparticle, with a different quark content. Fascinating as they are, the matter-antimatter oscillations of B0 mesons, either s or d type, do not by themselves imply that CP symmetry is violated. That happens only if the amplitude for a B0 meson to oscillate into a ¯B0 meson is unequal to the reversed process.
How can we hope to observe such an oscillation asymmetry? One way of monitoring the oscillations of B mesons is to observe decays that involve leptons, such as an electron or muon ( μ). We know that b quarks emit only μ- when they decay, while ˉb emit only μ+. The pˉp collision produces a matched pair of b and ˉb quarks, which may form a B0¯B0 pair, but never B0B0 or ¯B0 ¯B0. Thus, seeing two muons with the same charge is a sign that an oscillation has occurred prior to decay (see Fig. 1, top). The asymmetry of interest is simply [N(μ+μ+) − N(μ-μ-)]/[N(μ+μ+)+N(μ-μ-)].
The D0 detector is known for excellent muon detection, and the authors concentrate on this lepton only. Unfortunately, there are many other sources of background muons in the data, in addition to those from the desired B decays. Adding in many other μ+μ+ and μ-μ- pairs in equal numbers will “dilute” (reduce) the asymmetry due to the B0 oscillation and decay. An even more insidious effect is that these background muons can also have a CP asymmetry of their own. But this asymmetry is an uninteresting form of “environmental” CP violation, caused by the fact that the detector is made of matter and not antimatter. The systematic uncertainties associated with removing both the shift and the re-scaling between the raw measured asymmetry and the desired one are at the heart of this measurement.
The theoretical underpinning of the dimuon asymmetry in B decays is quite solid. The predicted excess of two positive muons over two negative muons, normalized to the sum, is Absl(SM)=(-2.3+0.5-0.6)×10-4. The raw asymmetry observed is A=(+56.4±25.1±5.3)×10-4. After corrections, the undiluted nonenvironmental asymmetry attributed to B mesons is Absl=(-73.6±26.6±30.5)×10-4. Tantalizing, perhaps, but this is not inconsistent with the standard model given the uncertainties. However, Abazov et al. have one final trick up their sleeves.
There should also be a charge asymmetry between single muons due to CP violation in the B mesons. Compared to the dilepton asymmetry, the B-physics effects in this single-lepton asymmetry are much more diluted and also even more sensitive to the “environmental” systematic shifts caused by the all-matter detector. The key argument is that the bulk of the systematic uncertainty caused by the detector effects is correlated between the dimuon and single-muon asymmetries. Thus, the authors create a linear combination of the two raw asymmetries, dimuon and single muon, that cancels much of the systematic shift and increases sensitivity to the B-physics effect of interest. After this manipulation, Abazov et al. obtain their final result: Absl=(-95.7±25.1±14.6)×10-4. This is 3.2 standard deviations removed from the standard model expectation. It is quite possible for new physics to alter the standard model prediction for B0 oscillations (see Fig. 1, bottom).
Abazov et al. present a number of cross-checks and consistency tests, which all lend support to pieces of the analysis. The longer Physical Review D article contains much detail. But there is no denying this is a complicated analysis that takes some study to appreciate. Evaluating systematic uncertainties is still partly an art form, with results that can depend on various inputs and assumptions. The authors include everything they believe is relevant, but independent confirmation is still essential.
There will be many opportunities for other experiments to weigh in on this physics. The CDF detector operating at the same accelerator has similar data to analyze. A new accelerator, the LHC at CERN in Geneva, Switzerland, will supply even more data in the near future; not only are there general purpose detectors, ATLAS and CMS, similar to D0 and CDF, but there is a B-physics detector as well: LHC-b. And plans are underway for a second generation of e+e- colliders dedicated to the study of b quarks.
If this intriguing hint of new physics holds up to scrutiny and is confirmed elsewhere, it will join other significant milestones of high-energy physics. Even if it fades away, it can still live on as part of a testament to the proper workings of empirical science. Indeed, the advent of modern scientific methodology, which forms the root of all our work, is the greatest milestone of all.
References
- V. M. Abazov et al. (D0 Collaboration), Phys. Rev. Lett. 105, 081801 (2010)
- V. M. Abazov et al. (D0 Collaboration), Phys. Rev. D 82, 032001 (2010)
- A.D. Sakharov, Pis’ma Zh. Eksp. Teor. Fiz. 5, 32 (1967)
- J. H. Christenson, J. W. Cronin, V. L. Fitch, and R. Turlay, Phys. Rev. Lett. 13, 138 (1964)
- B. Aubert and et al., Phys. Rev. Lett. 87, 091801 (2001)
- K. Abe and et al., Phys. Rev. Lett. 87, 091802 (2001)