The 5/2 enigma in a spin?
When a magnetic field pierces a (mostly) clean, two-dimensional electron system at very low temperatures, a plot of the Hall resistance of the electrons versus magnetic field looks like a staircase. The Hall resistance on each of the steps in the staircase—now famous as the manifestation of the integer and fractional quantum Hall effects—is precisely quantized at h/e2 divided by either an integer or a simple fraction. More than 70 fractions have so far been observed.
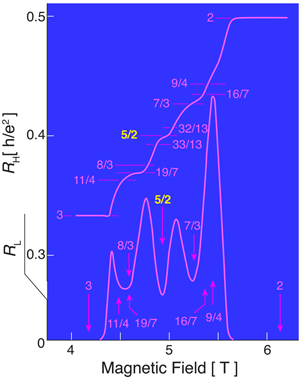
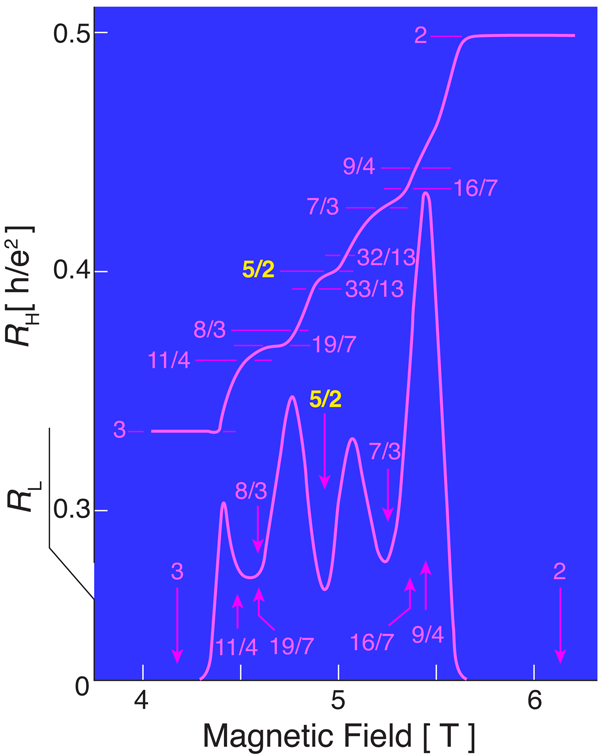
In this zoo of fractions, it may seem odd that the discovery in 1987 of a resistance plateau (Fig. 1) centered at filling factor ν=5/2 [1] could spark a more than twenty year effort to explain it. (The filling factor ν denotes the number of quantized Landau levels, formed by the magnetic field, that are filled.) Why all the hubbub about a single fraction? To appreciate this, we recall how the observation of more and more fractions has led to realizing the existence of quasiparticles with bizarre properties.
In the first report of what came to be known as the fractional quantum Hall effect, the Hall resistance plateau was quantized at h/e2 divided by 1/3. The theory explaining this effect led to the concept of “fractionalized” excitations that no longer behave like particles with a charge e but instead like complex particles with fractional charge e/3. They are also thought to provide a realization of particles obeying fractional statistics, called “anyons.” Anyons do not follow the normal commutation rules of Fermi or Bose particles, which are, respectively, odd or even under exchange. Instead, their exchange introduces a complex phase factor.
Subsequent experiments demonstrated a more extensive phenomenology, producing Hall resistance plateaus corresponding to long sequences of fractions given by the expression ν=n/(2pn±1), n and p being integers. Their theoretical explanation revealed that electrons capture quantized vortices to form particles known as “composite fermions.” Composite fermions do not see the external magnetic field but rather a much reduced effective magnetic field—they have, in a manner of speaking, swallowed up part of the external magnetic field. The integer quantum Hall effect for these composite fermions manifests as fractional quantum Hall effect for electrons at these fractions.
The model that takes composite fermions as weakly interacting does not produce fractional Hall states with an even denominator fraction, and new conceptual input is required. The leading theoretical contender for the ν=5/2 state, first put forth in 1991 by Gregory Moore (now at Rutgers University) and Nicholas Read (at Yale), predicts that the quasiparticles in this state obey non-Abelian braid statistics [2–4], and thus are even more complex than the Abelian anyons of the odd denominator states. While an esoteric concept, non-Abelian particles could have a real application in constructing qubits for fault tolerant topological quantum computation [5].
Moore and Read’s theory describes the ν=5/2 state in terms of a p-wave paired state of fully spin polarized composite fermions. This means that a test of whether this model is applicable could be found in an experiment that measures the spin polarization of the 5/2 state. Writing in Physical Review Letters, Michael Stern and colleagues at the Weizmann Institute of Science in Israel, with collaborators at the CNRS in Grenoble, France [6], probe the spin polarization by photoluminescence spectroscopy and find that, for their experimental conditions, the results are consistent with a state that is not spin polarized. This suggests that the physics of the 5/2 state may be even richer than previously thought, with a phase diagram containing both spin polarized and spin singlet states.
At filling factor ν=5/2, the lowest Landau level is fully occupied (contributing 2 to the filling factor) and the remaining electrons can occupy half of one spin band of the second Landau level. The physical picture that, over the years, has been developed to describe this state is based on several concepts [2–4]. The picture assumes that the ν=5/2 state arises from a Fermi sea of composite fermions, as is the case at the half-filled lowest Landau level. While no quantized Hall resistance plateau is seen at ν=1/2, there is a fractional quantum Hall effect at the filling of ν=5/2. To explain this difference, theory postulates that a pairing instability at 5/2 opens a gap in the composite fermion sea. If composite fermions are fully spin polarized, they must undergo a p-wave pairing. In the weak pairing phase, the Abrikosov vortices of the paired state support zero energy solutions that are symmetric combinations of the composite fermion creation and annihilation operators, called Majorana composite fermions. These particles obey non-Abelian statistics [2–4], and the Pfaffian wave functions of Moore and Read [2], which were motivated by conformal field theory, provide a concrete representation of this physics. The conceptual novelty of these ideas and the implications they may have on future technology have inspired a great deal of theoretical and experimental work aimed at finding definitive evidence for pairing of composite fermions as well as for the non-Abelian character of the excitations at ν=5/2.
Stern et al. directly determined the spin polarization of the 5/2 state (which occurs at a magnetic field of B∼4.3T for the electron density in their sample) with the technique of photoluminescence spectroscopy. This involves measuring the energy of the photon emitted by a conduction band electron in the lowest Landau level when it recombines with a valence band hole. The difference between the energies of the spectral lines for σ+ and σ- polarizations is given by the sum of the Zeeman energies of the electron in the conduction band and the hole in the valence band, plus a term ΔΣ that denotes the interaction of the lowest Landau level hole with the rest of the electrons. The term ΔΣ can be shown to be proportional to the spin polarization n↑-n↓ of the fermions in the fractional quantum Hall state. The principal finding of Stern et al. is that ΔΣ is vanishingly small at ν=5/2; that is, the fermions are not polarized.
Other experiments have searched for the spin polarization of the ν=5/2 state. For example, inelastic light scattering can detect the long wavelength spin wave mode at the Zeeman energy, which indicates a broken symmetry state with nonzero spin polarization. Rhone et al. [7] recently used this technique to investigate the 5/2 state, but the tell-tale spin wave was absent, indicating, like Stern et al.’s experiment, that the ν=5/2 state is not fully polarized.
Another approach is to apply a magnetic field within the plane of the two-dimensional electron gas, without changing the perpendicular field from satisfying the ν=5/2 condition. This additional parallel field increases the Zeeman energy of the spins, and if the composite fermions are spin polarized, the gap is expected to either increase or stay constant, depending on whether the excitation involves a spin flip or not—an effect that transport measurements should be able to detect. Several experiments have found, instead, that the transport gap of the 5/2 state decreases in a parallel field [8,9]. While initially taken as evidence that the ν=5/2 state is not spin polarized, the decay of the 5/2 fractional quantum Hall effect in these experiments is now understood as being caused either by a competing stripe phase or by physics related to the transverse thickness of the quantum wells.
In a recent unpublished work, Wei Pan and collaborators [10] at Sandia National Laboratories, the University of Florida, and Princeton University have taken an alternative approach: they vary the Zeeman energy by changing the magnetic field, but keep the two-dimensional system at ν=5/2 by controlling the sample density through a capacitive coupling to a frontgate electrode. They have found that the dependence of the gap, which increases with increasing magnetic field, in the magnetic field range of 2– 6.5T is consistent with a fully spin-polarized state. A significant observation in their earlier work, and by others, is that the ν=5/2 state persists at fields of up to B=10.4T [11] and 12.6T [12]. This is relevant because the Zeeman energy at these fields is large compared to the 5/2 gap, strongly suggesting that the 5/2 state here is fully spin polarized.
The issue of spin polarization is clearly of relevance to the physics of the 5/2 state. When it occurs at sufficiently high magnetic fields, the 5/2 state must surely be fully spin polarized. Even for small fields, numerical calculations make a good case for full spin polarization [13], but different experimental methods appear to lead to different conclusions. Certain open issues regarding Stern et al.’s experiment ought to be noted, however. The polarization maxima and minima are slightly offset from integer fillings, the origin of which is unclear. More importantly, the valence hole can be a strong perturbation, and may produce skyrmionlike excitations, as proposed by Wójs [14], thereby leading to a local spin depolarization. If true, it is possible that the conclusion relates to the local spin polarization in the vicinity of the hole rather than the global spin polarization of the 5/2 state. A Knight shift measurement by Tiemann et al. [15] finds a fully spin polarized 5/2 state.
Nonetheless, the experiments of Refs. [6,7] suggest the interesting possibility of two distinct 5/2 states, one which is spin polarized and one that is not. If so, this would raise obvious questions about the origin of the spin unpolarized 5/2 state, the phase boundary separating it from the polarized state, and the nature of the phase transition. It may lead the community to reconsider an s-wave pairing scenario that was proposed immediately following the discovery of the 5/2 state [16], as well as the role of disorder in creating spin depolarization [14]. A resolution to these questions would be important for identifying the region where non-Abelian statistics may occur.
Other aspects of the physical picture leading to non-Abelian anyons at 5/2 are also being tested. Several experiments [17–20] reported that the charge of the quasiparticle in the ν=5/2 state was e/4, as expected in Moore and Read’s theory. The e/4 charge is not, however, a proof of non-Abelian statistics. Experiments that measure the interference between quasiparticles traversing along different paths along the sample edges [19] and the tunneling conductance across a narrow junction [18] have sought to discriminate between various theoretical possibilities and also to reveal signatures of non-Abelian statistics. These experiments have all been analyzed assuming a fully polarized ground state.
Finally, we note that the 5/2 enigma belongs to a larger mystery surrounding the fractional quantum Hall effect in the second Landau level. The other observed fractions, such as 2+1/3, 2+2/3, 2+2/5, 2+3/5, match those observed in the lowest Landau level, but detailed calculations show, surprisingly, that the model of weakly interacting composite fermions, which is successful for the explanation of the lowest Landau level fractions, is not adequate for these second Landau level fractions. A resolution of the second Landau level fractional quantum Hall effect is likely to lead to much exciting physics.
Acknowledgments
Thanks are due to Steve Simon and Arek Wójs for their insightful comments, and to the DOE for financial support under Grant No. DE-SC0005042.
References
- R. L. Willett et al., Phys. Rev. Lett. 59, 1776 (1987)
- G. Moore and N. Read, Nucl. Phys. B 360, 362 (1991)
- N. Read and D. Green, Phys. Rev. B 61, 10267 (2000)
- C. Nayak and F. Wilczek, Nucl. Phys. B 49, 529 (1996)
- C. Nayak et al., Rev. Mod. Phys. 80, 1083 (2008)
- M. Stern, P. Plochocka, V. Umansky, D. K. Maude, M. Potemski, and I. Bar-Joseph, Phys. Rev. Lett. 105, 096801 (2010)
- T. D. N. Rhone et al., http://meetings.aps.org/link/BAPS.2010.MAR.Y2.3; and (unpublished)
- J. P. Eisenstein et al., Phys. Rev. Lett. 61, 997 (1988)
- C. R. Dean et al., Phys. Rev. Lett. 101, 186806 (2008)
- W. Pan et al. (unpublished)
- C. Zhang et al., Phys. Rev. Lett. 104, 166801 (2010)
- W. Pan et al., Solid State Commun. 119, 641 (2001)
- R. Morf, Phys. Rev. Lett. 80, 1505 (1998)
- A. Wójs et al., Phys. Rev. Lett. 104, 086801 (2010)
- L. Tiemann, G. Gamez, N. Kumada, and K. Muraki, in Proceedings of the 19th International Conference on the Application of High Magnetic Fields in Semiconductor Physics and Nanotechnology (HMF-19), Fukuoka, Japan, 2010 (unpublished)
- F. D. M. Haldane and E. H. Rezayi, Phys. Rev. Lett. 60, 956 (1988)
- M. Dolev et al., Nature 452, 829 (2008); arXiv:0911.3023v2
- R. L. Willett, L. N. Pfeiffer, and K.W. West, Proc. Natl. Acad. Sci. USA 106, 8853 (2009)
- I. P. Radu et al., Science 320, 899 (2008)
- V. Venkatachalam, A. Yacoby, L. Pfeiffer, and Ken West, arXiv:1008.1979 (2010)