Speeding up in a crowd
There is not a lot of “alone time” inside a cell. Rather, cellular biochemical reactions take place in a high concentration of reactant molecules and bystander macromolecules [1]. Interest in understanding reaction dynamics in the presence of such “crowded conditions” is now motivating theorists to extend the equations that have worked so well at describing reactions at low concentrations to a new regime [2,3]. In a paper appearing in Physical Review Letters, Nicolas Dorsaz at the University of Fribourg and colleagues at EPFL, both in Switzerland, and at Università di Roma La Sapienza, Italy, describe one approach to doing this that makes a step forward in predicting how reaction rates are affected by a high concentration of reactants [4].
When two reactant particles come together to form a product, there are two steps which can limit the rate at which the reaction occurs [3]. The first is the formation of an intermediate product, known as the “transient” or “encounter” complex, which consists of configurations in which the reactant particles have relative separations and orientations close to those in the final product. The second potential rate-limiting step occurs when the reactant molecules, starting from the transient complex, undergo configurational rearrangements to form the final product.
Reactant particles approach the first step through translation and rotation, motions that, in solution, are generally diffusive. For this reason, biomolecular reactions where the formation of the transient complex limits the rate of reaction are said to be diffusion-limited.
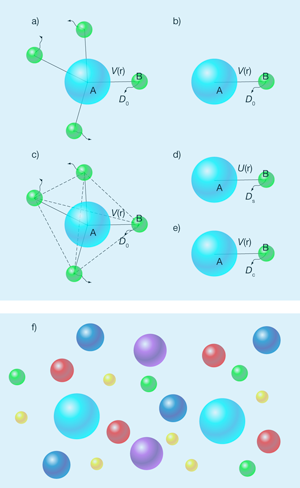
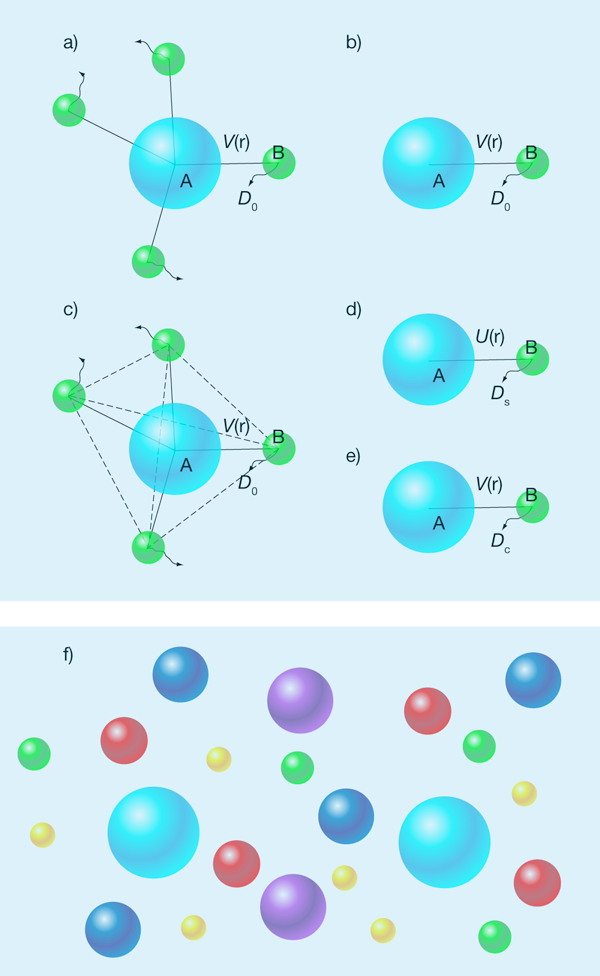
A theoretical framework for modeling diffusion-limited bimolecular reactions was established by the Polish scientist Marian Smoluchowski [5] nearly a century ago. When a single reactant particle, labeled , is surrounded, at time , by an equilibrium distribution of reactant particles, labeled [Fig. 1(a)], the survival probability of particle at time satisfies
Here, is the bulk concentration of the reactant, and is a time-dependent rate coefficient, which is determined by the so-called distribution function, , of an - reactant pair. For reactions between spherical particles, only relative motion between the particles matters and the distribution function satisfies the Smoluchowski equation:
where denotes the inverse thermal energy, is the translational diffusion constant of a reactant particle relative to the reactant particle, and is their interaction energy [Fig. 1(b)]. Without the two factors containing , Eq. (2) is just the usual diffusion equation. The two extra factors in the Smoluchowski equation account for the fact that the interparticle relative diffusion is under the influence of their interaction energy. A diffusion-limited reaction between and is modeled by an absorbing boundary condition—that is, one where the distribution function is zero—when the two reactant molecules are in contact. The rate coefficient is given by the total flux of the pair-relative diffusion across the contact surface.
The Smoluchowski theory reduces a many-body problem to essentially a one-body problem [Fig. 1(a) and (b)]. It is strictly valid only if the reactant particle is immobile, the reactant particles do not interact with each other, and motions of the particles are diffusive over all timescales. However, when the concentration of the reactant increases, the interactions between them can’t be ignored [Fig. 1(c)]. As a result, there have been various attempts to extend or modify the Smoluchowski theory to account for these interactions.
One approach [6,7] is based on the assumption that the pair distribution function is still governed by the Smoluchowski equation, but the - pair interaction potential is replaced by , the potential of mean force for the pair [Fig. 1(d)]. The potential of mean force accounts for the effect of the other particles (and other bystander solute particles if present) on the interaction of the - pair. Similarly, the effects of the other particles on the diffusion constant are accounted for by replacing with the self-diffusion constant . Self-diffusion of a particle is slowed down by the presence of other hard particles; hence [8].
This extended Smoluchowski approach was tested against simulation results of a system of hard-sphere particles where the volume fraction of the particles (reactants and bystanders) was , which is a high concentration [9]. In the simulations, one particle was labeled as , various numbers of other particles labeled as , and the remaining particles were bystanders. Up to moderate concentrations of the reactant (less than volume fraction), predictions of the survival probability by the extended Smoluchowski approach agreed well with the simulation results. At higher fractions, however, the predictions underestimated the decay rate of the survival probability.
Another approach, which is what Dorsaz et al. follow, is based on the “local concentration,” , of the particles around the particle [9]. The local concentration also satisfies Eq. (2), but with replaced by the so-called collective diffusion constant, [9,10] [Fig. 1(e)]. The latter depends on the local concentration and is given by [10]
where is the local mobility, and is the local osmotic pressure. If hydrodynamic interactions between the particles are absent, then . When , the effects of interactions between the particles are negligible, and consequently . In this limit, . When for hard particles. That is, the collective diffusion constant of the reactant is greater than the diffusion constant of a single particle in the dilute limit. This is in contrast to the self-diffusion constant , which, as noted above, is smaller than . The collective diffusion flux across the - contact surface is taken to be . The steady-state rate constant predicted from the linearized Smoluchowski equation for agrees well with simulation results up to moderate concentrations (less than for hard particles) [9].
In their paper, Dorsaz et al. push this theoretical approach and simulations to higher concentrations. For the case where there is no interaction between the particles , they found by solving the steady-state Smoluchowski equation for without approximation and tested the solution against simulations. The system they simulated consisted of an immobilized particle with an absorbing contact surface, surrounded by diffusing particles. All the particles were hard spheres. The theory agreed well with the simulations, provided the particle was much larger than the particles. Relative to the dilute limit, Dorsaz et al. found an eightfold increase in at high reactant concentrations. However, when the particle was smaller than the particles, the theory significantly overestimated at high concentrations.
Dorsaz et al.’s study brings attention to an important question: What is the appropriate governing equation for modeling bimolecular reactions at high reactant concentrations? Up to moderate concentrations, both of the approaches outlined above are supported by simulations. However, both exhibit some failings at high reactant concentrations. The approach based on collective diffusion seems to work at high reactant concentrations at least when the particle is much bigger than the particles. Dorsaz et al. attempted to remedy the problem with the theory when the particle was smaller than the particles by introducing an effective interaction potential (along with additional improvisations). However, this remedy is ad hoc and apparently double counts the effects of the other particles on the pair potential, since these effects are supposed to have already been captured by the collective diffusion constant. It is also unclear how the governing equation for the local concentration should be modified when other bystander particles are present. For example, Dorsaz et al. found a significant decrease in when just a tiny fraction of the particles were replaced by bystanders.
Since understanding reactions in cells is a motivating factor in these kinds of studies, it is important to point out a crucial difference between the condition simulated by Dorsaz et al. and that inside cells. While the total concentration of intracellular macromolecules is very high, the concentration of each individual species is actually quite low [Fig. 1(f)]. Ultimately, theories and simulations will have to be tailored to this condition to be of physiological relevance.
Acknowledgments
Research support from NIH Grants GM58187 and GM88187.
References
- S. B. Zimmerman, and S. O. Trach, J. Mol. Biol. 222, 599 (1991)
- H.-X. Zhou, G. Rivas, and A. P. Minton, Ann. Rev. Biophys. 37, 375 (2008)
- G. Schreiber, G. Haran, and H.-X. Zhou, Chem. Rev. 109, 839 (2009)
- N. Dorsaz, C. De Michele, F. Piazza, P. De Los Rios, and G. Foffi, Phys. Rev. Lett. 105, 120601 (2010)
- M. V. Smoluchowski, Z. Phys. Chem. 92, 129 (1917)
- H.-X. Zhou, and A. Szabo, J. Chem. Phys. 95, 5948 (1991)
- H.-X. Zhou, J. Mol. Recog. 17, 368 (2004)
- Technically, the self-diffusion of a B particle exhibits different behaviors at short and long times. The dividing line between the two regimes is the average time for the particle to traverse a distance equal to the particle size. On average, a B reactant particle must move over a distance much longer than the particle size before it reacts with the A reactant to form the product. Therefore here denotes the long-time self-diffusion constant. Similarly, , introduced below, denotes the long-time collective diffusion constant
- J. Dzubiella, and J. A. McCammon, J. Chem. Phys. 122, 184902 (2005)
- J. K. G. Dhont, An Introduction to Dynamics of Colloids (Elsevier, Amsterdam, 1996)[Amazon][WorldCat]