Towards superconductor-spin ensemble hybrid quantum systems

Tim Duty

Viewpoint

Towards superconductor-spin ensemble hybrid quantum systems

Centre for Engineered Quantum Systems, School of Mathematics and Physics, The University of Queensland, St. Lucia, Queensland 4072, Australia

September 27, 2010• Physics 3, 80

Ensembles of dilute spin impurities in condensed matter systems can be accessed using microelectronic circuits and therefore may offer a way for long-term storage and enhanced processing of quantum information.

Figure caption — **Figure 1:** Example of how spin packets in a condensed matter system can be accessed and studied, adapted from Kubo *et al.* [4]. A diamond slab containing nitrogen-vacancy center spins (arrows) is positioned above a microfabricated superconducting resonator. A magnetic field $B_{NV}$ is applied as shown to tune the $NV$ centers. A microwave signal excites a mode in the resonator with magnetic field $B_{r}$ to manipulate and probe the spin ensemble.

Complex information systems, whether natural or manmade, rely on specialization of functionality in order to efficiently carry out information processing tasks. In the quintessential model used by computer scientists, called the Turing machine, computation proceeds using a “tape,” or long term memory, and a “processor” that consists of a malleable state register coupled to a read/write head. Today’s computers use transistors to manipulate charge on a capacitor for fast processing and a collection of magnetic domains on a hard drive for long term information storage or “non-volatile memory.” It is inevitable that future quantum processors will follow a similar path, and take advantage of different physical systems in order to trade off the capability of strong quantum control for long coherence times.

Physical implementations of quantum bits, or “qubits,” span the range from microscopic systems such as trapped atoms (or ions) and electron and nuclear spins, to large mesoscopic devices based upon Josephson junctions. Isolated trapped atoms, as well as electron and nuclear spins, are naturally protected from decoherence due to weak coupling to their environments. This can be understood as due to the relative smallness of atomic dipoles, or in the case of spins, a weak magnetic-only coupling. One must apply very large electric or magnetic fields to appreciably shift their energies. This makes control, readout, and most importantly, two-qubit gates using individual atoms or spins very slow and difficult to achieve. Josephson junction qubits [1], on the other hand, couple very strongly to external fields, allowing fast manipulation and direct interfacing to electrical circuits. For example, a single charge-based superconducting qubit can have a dipole moment that exceeds $10^{4}$ atomic dipoles, and a flux-based superconducting qubit comprises a superposition of two states that each carry a magnet moment of $\sim 10^{6}$ Bohr magnetons. This allows for very strong and robust control, readout, and coupling, but despite very hard work to engineer the environment, one must pay the price of much reduced coherence times compared to microscopic systems [2]. For this reason, many groups are pursuing the development of hybrid quantum systems, where it is envisioned that fast qubit gate operations will be performed using superconducting qubits, and memory registers will be implemented using microscopic atomic systems. In addition to quantum information processing, one expects such hybrid systems to open up new avenues of research in quantum phenomena, as well as enable new forms of quantum metrology and novel sensors. In order to proceed, however, one must develop a high-fidelity quantum “transducer” that exchanges quantum information between the atomic memory and the superconducting processor. This can be conveniently implemented by the exchange of photons held in a high quality-factor cavity.

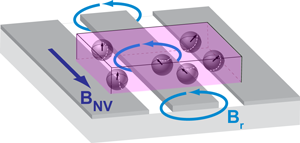
The most robust Josephson junction qubits use the superconductor aluminum, which has a superconducting gap of $\sim 200 \times 10^{- 6} eV$ . In order not to create excitations above the superconducting gap, one should probe these systems with photons below this energy scale, and therefore Josephson-junction qubits typically are constructed with transition energies corresponding to photons of order $10 GHz$ . In other words, they operate at microwave frequencies. A very compatible quantum memory could be a collection of electron spins, since their spin splittings are typically at microwave frequencies in magnetic fields small enough not to kill the superconductivity. Larger magnetic fields can be used if the magnetic field is oriented parallel to the superconducting films. Microwave photons, therefore, could act as a bridge between naturally occurring electron spin systems and the fabricated electrical circuits that are used to build Josephson-junction qubits. Electron spin impurities such as nitrogen vacancies (NV centers) [3] or other atomic centers residing in solids are more physically compatible with superconducting qubits than isolated atomic systems, since coupling these to microfabricated chips does not require difficult trapping techniques. One can easily integrate such solid-state systems with the chip containing the superconducting qubits.

Writing in Physical Review Letters, two groups—Yuimaru Kubo and colleages at several institutions in France and Germany [4], and David Schuster and colleagues at universities in the US and the UK [5]—report experiments that demonstrate the coupling of microfabricated superconducting resonators to impurity spin ensembles containing $\sim 10^{12}$ electron spins. These experiments show exchange of microwave photons between the resonator and the spin ensemble, which is evident in an observed vacuum Rabi splitting, or photon exchange frequency, that both exceeds the resonator linewidth and is comparable to the spin ensemble linewidth. Similar superconducting resonators are used in so-called “circuit-QED” experiments with superconducting qubits. The advantage of using such microfabricated resonators comes with the possibility of achieving tiny mode volumes [6]. Schuster et al. report measurements using both impurity ${Cr}^{3 +}$ spins in sapphire ( ${Al}_{2} O_{3}$ : ${Cr}^{3 +}$ , or ruby), and $N$ substitution ( $P 1$ ) centers in diamond, while Kubo et al. describe measurements of nitrogen-vacancy (NV) centers in diamond (Fig. 1). The NV centers studied by Kubo et al. are particularly interesting due to the added possibility of microwave to optical up-conversion using this system [7].

The loss incurred in exchanging a photon between the resonator and spin ensemble is characterized by a measure denoted $C$ , the “cooperativity,” which can be thought of as the departure from unity efficiency in moving a photon from the resonator into the spin ensemble. Both Kubo et al. and Schuster et al. find cooperativities exceeding $10$ ( $27$ and $11.5$ , respectively), which indicate photon losses of $0.2$ – $0.4 dB$ . These values of $C$ are of the same order of magnitude as that recently achieved using trapped ions in an optical cavity [8], although very much fewer ions ( $N \sim 10^{3}$ ) were involved. On the other hand, they are many order of magnitudes lower than the cooperativity attained using optical cavities containing Bose-Einstein condensates of $\sim 10^{3}$ – $10^{5}$ atoms [9]. One could boost the values of $C$ in solid-state spin systems by using higher quality-factor field modes, such as microwave whispering gallery modes in dielectric resonators [10]; however, the real challenge to implementing a spin-based quantum memory is to find spin systems with much narrower linewidths.

A step in this direction is explored in a third Letter by Hua Wu and colleagues in the UK, Denmark, US, and Japan [11] who also demonstrate how such narrow linewidth spin ensembles can be used to store weak microwave pulses using conventional ESR techniques. In addition, they are able utilize the hyperfine interaction between electron and nuclear spins to transfer multiple pulses into and out of a nuclear spin degree of freedom. Their experiments use the electron spins in bulk samples of endohedrally doped nitrogen fullerene ( $^{14} N @ C_{60}$ ) at room temperature, and phosphorous ( $P$ donor) spins in silicon at $9 K$ . Wu et al. show how multiple excitations can be stored in distributed spatial modes as in holography. The extension of their work to storing single microwave photons seems favorable, although to achieve this will remain a significant experimental milestone for future experiments. Using the electron spin ensemble, the memory time in the experiments of Wu et al. is limited to several hundreds of microseconds. Although this greatly exceeds the coherence times of superconducting qubits, one can do even better by storing information in nuclear spins, where coherence times of seconds are possible. Wu et al. demonstrate this concept by transferring an entire eight-pulse state stored in an electron spin ensemble of $P$ donors in isotopically enriched $^{28} Si$ (zero nuclear spin) to the $P$ nuclear spins, and then back to the electron spins, and finally back to the measurement electronics as a spin echo.

Taken together, the results described by Kubo et al., Schuster et al., and Wu et al. point the way towards more complex models of solid-state quantum information processing and unique possibilities for studying novel quantum phenomena at the interface between heterogeneous physical systems. The coupling of mesoscopic quantum bits, which work at microwave frequencies, to atomic systems, which have optical transitions, may also lead to coherent coupling of single-photon microwaves to those of visible light, therefore enabling distributed quantum information processing.

Note added by author (5 October 2010): Recently, another group in the US, Chiorescu et al. [12], used a cavity ESR technique similar to Wu et al. [11] to show strong coupling between microwave photons and an ensemble of spins, similar to the finding of Kubo et al. [4] and Schuster et al. [5]. The spin ensemble used by Chiorescu et al. consists of $\sim 10^{20}$ isotropic spins with $S = 1 / 2$ in dipheriyl-picri-hydrazyl (DPPH), a field calibration standard.

References

See J. Q. You and F. Nori, Phys. Today, 58, No. 11, 42 (2005) and references therein; John Clarke and Frank K. Wilhelm, Nature 453, 1031 (2010)
Note, however, that there has been some success in designing superconducting qubits to be insensitive to low-frequency charge noise. See J. Koch et al., Phys. Rev. A 76, 042319 (2007); and V. E. Manucharyan et al., Science 326, 113 (2009)
F. Jelezko et al., Phys. Rev. Lett. 92, 076401 (2004)
Y. Kubo, F. R. Ong, P. Bertet, D. Vion, V. Jacques, D. Zheng, A. Dréau, J-F. Roch, A. Auffeves, F. Jelezko, J. Wrachtrup, M. F. Barthe, P. Bergonzo, and D. Esteve, Phys. Rev. Lett. 105, 140502 (2010)
D. I. Schuster, A. P. Sears, E. Ginossar, L. DiCarlo, L. Frunzio, J. J. L. Morton, H. Wu, G. A. D. Briggs, B. B. Buckley, D. D. Awschalom, and R. J. Schoelkopf, Phys. Rev. Lett. 105, 140501 (2010)
See R. J. Schoelkopf and S. M. Girvin, Nature 451, 664 (2008) and references therein
G. D. Fuchs et al., Nature Phys. 6, 668 (2010)
P. F. Herskind et al., Nature Phys. 5, 494 (2009)
F. Brennecke et al., Nature 450, 268 (2007); Y. Colombe et al., 450, 272 (2007)
D. L. Creedon et al., Phys. Rev. B 82 104305(2010)
H. Wu, R. E. George, J. H. Wesenberg, K. Mølmer, D. I. Schuster, R. J. Schoelkopf, K. M. Itoh, A. Ardavan, J. J. L. Morton, and G. A. D. Briggs, Phys. Rev. Lett. 105, 140503 (2010)
I. Chiorescu, N. Groll, S. Bertaina, T. Mori, and S. Miyashita, Phys. Rev. B 82, 024413 (2010)

About the Author

Tim Duty is a Senior Lecturer in the School of Mathematics and Physics at The University of Queensland in Australia. He received his Ph.D. from The University of British Columbia in 2000, and worked for several years as a researcher at Chalmers University of Technology in Sweden before moving to Australia. His primary research interests at present center around the implementation of quantum optics and quantum metrology using microwaves and superconducting devices. In his spare time he enjoys flying sailplanes.

Strong Coupling of a Spin Ensemble to a Superconducting Resonator

Y. Kubo, F. R. Ong, P. Bertet, D. Vion, V. Jacques, D. Zheng, A. Dréau, J.-F. Roch, A. Auffeves, F. Jelezko, J. Wrachtrup, M. F. Barthe, P. Bergonzo, and D. Esteve

Phys. Rev. Lett. 105, 140502 (2010)

Published September 27, 2010

Read PDF

High-Cooperativity Coupling of Electron-Spin Ensembles to Superconducting Cavities

D. I. Schuster, A. P. Sears, E. Ginossar, L. DiCarlo, L. Frunzio, J. J. L. Morton, H. Wu, G. A. D. Briggs, B. B. Buckley, D. D. Awschalom, and R. J. Schoelkopf

Phys. Rev. Lett. 105, 140501 (2010)

Published September 27, 2010

Read PDF

Storage of Multiple Coherent Microwave Excitations in an Electron Spin Ensemble

Hua Wu, Richard E. George, Janus H. Wesenberg, Klaus Mølmer, David I. Schuster, Robert J. Schoelkopf, Kohei M. Itoh, Arzhang Ardavan, John J. L. Morton, and G. Andrew D. Briggs

Phys. Rev. Lett. 105, 140503 (2010)

Published September 27, 2010

Read PDF