Liquid-crystalline phases of ultracold atoms
When atoms move in a standing wave created by two counterpropagating laser beams, they experience a periodic potential. This potential arises because the electric field in the standing wave induces an electric dipole in the atoms, which in turn seek out the most intense regions of electric field. Atoms in optical lattice potentials can simulate a variety of condensed matter phenomena including, most notably, the transition between superfluid and Mott insulator states in Bose systems [1].
The possibilities expand when the atoms are placed in an optical cavity, where they can coherently scatter light and influence the confining potential. In these strongly nonlinear systems, the atoms and cavity light field can conspire to produce novel phase transitions, where the atoms self-organize into crystalline phases [2–6]. In a paper appearing in Physical Review A, Sarang Gopalakrishnan, Benjamin Lev, and Paul Goldbart at the University of Illinois, Urbana-Champaign [7], have developed a comprehensive theoretical scheme to explore the behavior of atoms coupled to a continuum of cavity modes. Building upon earlier work [8,9], they explore the unique characteristics of crystalline and superfluid phases formed in optical cavities, the nature of the transitions between these phases, and how these phases might relate to the phenomenon of supersolidity.
When the configuration of the atoms is determined self-consistently by the scattered light field, the range of steady-state phases and collective dynamics is rich. The behavior of atoms and light in this “self-organized” optical lattice system draws together elements from the fields of quantum optics and ultracold atomic physics. These include understanding how a mechanical degree of freedom (the atomic motion) couples to light [10] and how, as a result of nonlinear feedback, light fields can switch between two different stable states (optical bistability) [11]. Moreover, these atom-cavity systems naturally provide access to the correlations and dynamics of self-organization because light leaving the cavity can be monitored in situ [12].
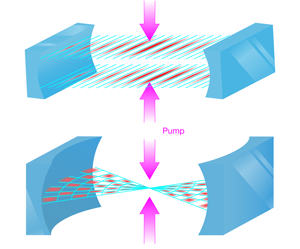
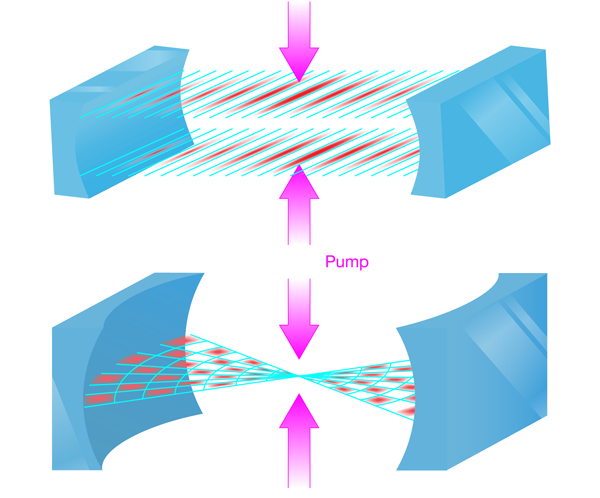
The theoretical work of Gopalakrishnan et al. is particularly timely in view of recent experiments [13] performed by Tilman Esslinger’s group at the ETH in Switzerland, which showed how atoms self-organize in a single-mode optical cavity. In these experiments, the team coupled a Bose-Einstein condensate of atoms to the light field in an optical cavity. A pump laser, directed perpendicular to the cavity axis, maintained the light field in the cavity and the atoms scattered light from the pump laser to the cavity mode (see setup in Fig. 1, top). When the pump laser was above a critical intensity, the system underwent a transition to a state with a periodically modulated atom density, sustained by a standing wave of light in the cavity direction. An interesting feature of this experiment is that it can be understood [14,15] as a realization of the long-sought phase transition of the Dicke model, an archetypal model for coupled matter-light systems. This phase transition involves the breaking of a discrete, twofold symmetry between the two possible sublattices of the single cavity mode that can be populated by the atoms.
Gopalakrishnan et al. investigate how the phase behavior of an atom-cavity system is affected when, rather than a single cavity mode, there is a continuum of possible modes for the light field (Fig. 1, bottom). In this case, the transition to the ordered phase is associated with the breaking of a continuous translational symmetry, which is what happens in conventional crystalline ordering. In particular, the authors consider a “pancake” geometry in which a two-dimensional cloud of atoms is confined in a confocal cavity. In this geometry, the “continuum” is supplied by the large number of degenerate, or almost degenerate, optical modes. As in the experiments by the ETH group, the external pump singles out the set of modes that determine the self-organization of the atoms. Since this arrangement involves the breaking of a continuous symmetry, it opens up the possibility to study many aspects of crystallization, such as the behavior of defects, the growth and arrangement of crystal grain boundaries, and the nature of the phonon spectrum.
In contrast to most solids, crystallization in this multimode cavity geometry is not described by the usual Landau theory of crystallization [16]. Rather, as Gopalakrishnan et al. argue, the transition they study falls into the class of “Brazovskii transitions” that were explored in connection with liquid crystals [17], and later, in relation to the patterns that form at convective instabilities [18]. Unlike the Landau theory, where the free energy of a system is assumed to have a cubic term that breaks the symmetry at the phase transition, no such term exists in the free energy for systems described by a Brazovskii transition. The result is that “crystallization” in a Brazovskii transition involves a transition to a layered (smectic) liquid-crystal phase (rather than to a hexagonal crystal lattice). Similarly, in the cold atomic system that Gopalakrishnan et al. study, the long-lived cavity modes have no cubic coupling, hence the transition is of the Brazovskii type.
As well as providing a platform to explore the characteristic features of crystallization described by the Brazovskii transition, the present system of atoms in multimode cavities also allows one to explore aspects not present in contexts such as liquid crystals. In particular, it potentially allows access to symmetry breaking in two distinct regimes depending on the pump and the decay rate of the cavity modes. If pumping and decay are weak then one can explore the zero-temperature phase transition; if pumping and decay are stronger, then the transition is dominated by the noise they induce. For sufficiently small pump and decay rates, the authors study the quantum version of the Brazovskii transition. Using both renormalization group theory as well as more phenomenological approaches, the authors show that quantum fluctuations do not destroy classical behavior and that the transition remains discontinuous. The effects of pump and decay, if present, will always determine the behavior of the system at the lowest energies, however quantum fluctuations could potentially be relevant at intermediate energy scales.
As with the experiment performed at ETH, the atoms in the cavity may maintain their coherence even inside the crystallized phase. In this case, Gopalakrishnan et al. show that the crystalline state is a supersolid, or as they more accurately term it, a “supersmectic” phase, as there is liquid-crystalline, rather than crystalline, order. It is interesting to consider how this form of supersolidity is affected as the self-generated optical lattice becomes deeper. In the case of the single-mode cavity, theoretical work [19] predicts a transition from the coherent to an incoherent state of the self-organized system, analogous to the superfluid-Mott insulator transition studied in an externally imposed optical lattice [1]. Since the Brazovskii transition leads to a discontinuous jump of the optical lattice strength, Gopalakrishnan et al. point out that this can change the morphology of the phase diagram. This allows for the intriguing possibility of a direct superfluid-solid transition, as well as a superfluid-supersolid-solid sequence.
Gopalakrishnan et al. have elucidated a rich variety of phase behavior and physical phenomena that can be realized by ultracold atoms in multimode optical cavities. This allows for the possibility of studying supersolid to solid transitions, fundamental aspects of crystallization, and topological defects in liquid crystals. The coupled atom-light system also gives rise to rich opportunities to explore zero temperature quantum fluctuations and crystallization, or nonequilibrium phase transitions. This work also suggests connections to optical bistability, associated with the discontinuous nature of the transition, of a kind rather far from many previous optically bistable systems. The wealth of possibilities emerging from this study show that the self-organization of atoms in cavities will provide a new arena where experiments can explore and discover properties of crystalline and liquid-crystalline ordering.
References
- M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, and I. Bloch, Nature 415, 39 (2002)
- P. Domokos and H. Ritsch, Phys. Rev. Lett. 89, 253003 (2002)
- A. T. Black, H. W. Chan, and V. Vuletić, Phys. Rev. Lett. 91, 203001 (2003)
- J. K. Asbóth, P. Domokos, H. Ritsch, and A. Vukics, Phys. Rev. A 72, 053417 (2005)
- D. Nagy, J. K. Asbóth, P. Domokos, and H. Ritsch, Europhys. Lett. 74, 254 (2006)
- D. Nagy, G. Szirmai, and P. Domokos, Eur. Phys. J. D 48, 127 (2008)
- S. Gopalakrishnan, B. L. Lev, and P. M. Goldbart, Phys. Rev. A 82, 043612 (2010)
- S. Gopalakrishnan, B. L. Lev, and P. M. Goldbart, Nature Phys. 5, 845 (2009)
- H. Ritsch, Nature Phys. 5, 781 (2009)
- F. Brennecke, S. Ritter, T. Donner, and T. Esslinger, Science 322, 235 (2008)
- L. A. Lugiato, Prog. Opt. 21, 69 (1984)
- W. Chen, D. Meiser, and P. Meystre, Phys. Rev. A 75, 023812 (2007); I. B. Mekhov, C. Maschler, and H. Ritsch, Nature Phys. 3, 319 (2007)
- K. Baumann, C. Guerlin, F. Brennecke, and T. Esslinger, Nature 464, 1301 (2010)
- F. Dimer, B. Estienne, A. S. Parkins, and H. J. Carmichael, Phys. Rev. A 75, 013804 (2007)
- D. Nagy, G. Konya, G. Szirmai, and P. Domokos, Phys. Rev. Lett 104, 130401 (2010)
- L. D. Landau, Sov. Phys. JETP 7, 627 (1937)
- S. Brazovskii, Sov. Phys. JETP 41, 85 (1975)
- J. Swift and P. Hohenberg, Phys. Rev. A 15, 319 (1977)
- S. Fernández-Vidal, G. De Chiara, J. Larson, and G. Morigi, Phys. Rev. A 81, 043407 (2010)