Forty years of Efimov physics: How a bizarre prediction turned into a hot topic

This year, we celebrate the fortieth anniversary of a bizarre theoretical prediction made by Vitaly Efimov. In 1970, the young Russian physicist worked at a nuclear physics institute in Leningrad and he was attracted by the challenging three-body problem in quantum physics [1]. He was inspired by theoretical work of L. H. Thomas, published in 1935, on the triton (the nucleus of the tritium atom) as a fundamental three-body system [2]. Efimov focused his attention on the situation of three identical bosons with resonant two-body interactions [3,4].

The essential condition for this resonant regime can be discussed in terms of the $s$-wave scattering length $a$. At very low energies, when other partial waves do not contribute, the parameter $a$ characterizes the quantum-mechanical interaction between two particles. Elastic collisions then take place like between tiny billiard balls of radius $|a|$, and the sign of $a$ contains additional information on the phase shift of the wave function. The resonant regime is realized in situations where $|a|$ is large compared to the characteristic range over which two particles interact, e.g., the strong interaction for nucleons or the van-der-Waals interaction for neutral atoms. This regime also means that a two-body bound state is very close to the zero-energy threshold, either a very weakly bound true dimer state (for $a>0$) or a state just disappearing in the scattering continuum ( $a<0$).

The resonant two-body interaction condition also greatly simplifies the physics of the three-body problem. It becomes universal in the sense that details of the short-range interaction become irrelevant except for an additional quantity, the so-called three-body parameter. The problem is then fully characterized by just two parameters, no matter whether nucleons, atoms, or other resonantly interacting particles are considered—Efimov was studying a very general phenomenon.

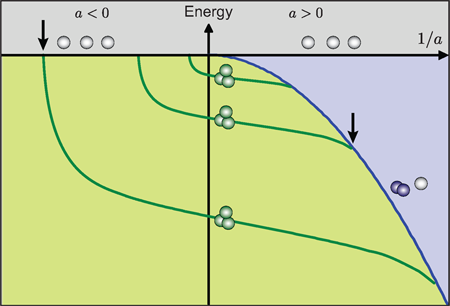
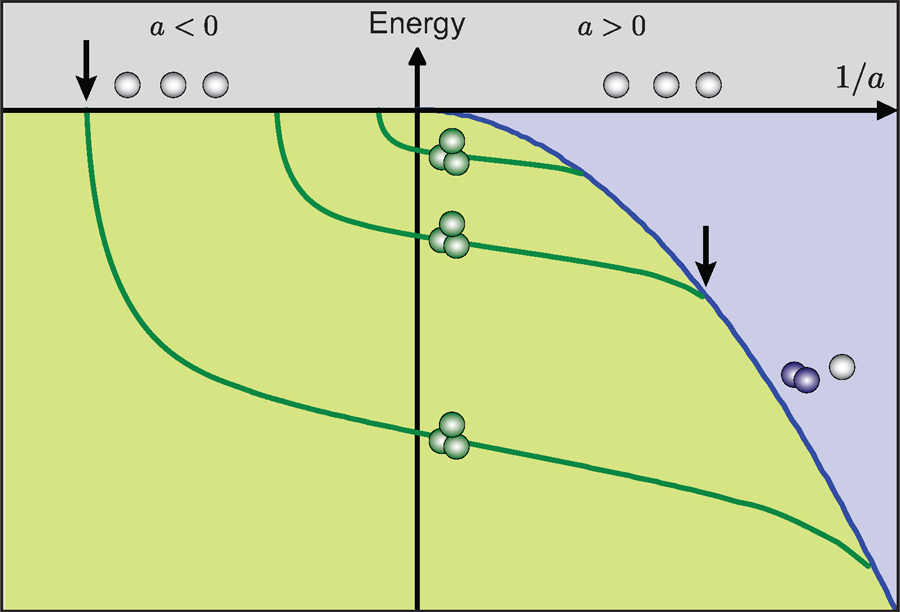
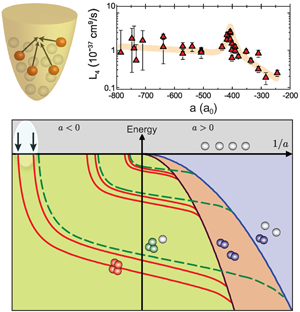
The basic scenario he considered is illustrated in Fig.1, where the energy of three atoms is plotted versus the inverse scattering length $1/a$. To understand this picture, let us first consider the different regions as separated by corresponding thresholds. For $E>0$ (grey region) the system consists of three free atoms with some kinetic energy. Below the zero-energy threshold (marked by the solid horizontal line for $E=0$) bound states must be involved. For $a>0$, a weakly bound dimer state exists with energy $-{\mathrm{ħ}}^2/(m{a}^2$), where $m$ is the atomic mass and $\mathrm{ħ}$ is Planck’s constant divided by $2\pi$. In the three-body picture, this dimer state leads to the atom-dimer threshold, above which a dimer coexists with a free atom (blue region). The region of interest for Efimov states (green region) is below the triatomic threshold for $a<0$ and below the atom-dimer threshold for $a>0$, where only bound trimer states can exist.

×

In his solution, Efimov found a series of “giant’” trimer states (dark green lines) that connect from the triatomic threshold at $a<0$ to the atom-dimer threshold at $a>0$. He also found a surprising geometric scaling law, containing a factor $22.7$ (essentially $e^{\pi }$ with a small correction). Increasing the length scale by a factor of $22.7$, another state is found with a size $22.7$ times larger and an energy smaller by a factor of $22.7^2$. Further intriguing and counterintuitive properties are that (i) for $a<0$, three-body bound states (so-called Borromean states in which, like the famous Borromean rings, removing any one of the three components destroys the whole) exist in the absence of any two-body bound state, and (ii) for $a>0$, the trimer states vanish with increasing strength of the two-body bond. The role of the three-body parameter in this scenario is just to determine where exactly the series of states begins.

Researchers are fascinated by Efimov states and have invested effort in studying them for three main reasons: Their bizarre and counterintuitive properties, the paradigmatic role of Efimov’s scenario for the concept of universality in few-body physics, and the extraordinary challenge to observe them experimentally.

Efimov recently described the evolution triggered by his prediction with the words “from questionable to pathological to exotic to a hot topic” [5]. In the first years, theorists verified his prediction in different ways (see, e.g., Ref. [6]). Some of them apparently were motivated by proving him wrong, but they did not arrive at the expected result, finally confirming Efimov’s prediction.

The Efimov effect has attracted considerable attention in relation to halo states in atomic nuclei [7]. States with Borromean character are well established in nuclear physics, but Efimov states have not been found. A severe complication in nuclei is the Coulomb interaction, which prevents the appearance of Efimov states and thus strongly constricts the candidate systems. In nuclear systems, Efimov states may be found in neutron-rich nuclei [8] and neutron scattering experiments [9].

Since 1977 the helium trimer has been considered an interesting and fundamental candidate for Efimov states in molecular physics [10]. About $50$ theoretical publications were dedicated to this problem, but the experiments on molecular beams could not confirm the expectations; they rather raised doubts on the existence of Efimov states in helium [11]. Other molecules were discussed as candidates for Efimov states [12], but so far without any experimental verification. The observation of Efimov states thus remained an elusive goal for $35$ years.

In the late 1990s, the advent of Feshbach resonances with the new ability to tune interactions in ultracold gases triggered growing interest in Efimov states in the ultracold community (see, e.g., Ref. [13]). Already in 1999, a group at Stanford (led by the 1997 Nobel laureate Steven Chu, now the US Secretary of Energy) speculated about possible signatures of Efimov states in their experiments on cesium atoms [14] and, indeed, as it turned out later, they came close to it.

In ultracold gases, the collision energies are extremely low (typically in the pico- $\text{eV}$ range), so that interactions are dominated by $s$-wave scattering and higher partial waves can be neglected. In this case, the $s$-wave scattering length $a$ fully characterizes the two-body interaction.

A resonance phenomenon, known as “Feshbach resonance” provides experimentalists with the unique possibility of controlling the two-body interaction via an external magnetic field. Feshbach resonances have been predicted for ultracold gases in the early 1990s [15] and were first observed in 1998 [16,17]. Since then they have developed into an essential tool for many applications in ultracold atom physics (see Ref. [18] for a review). Thanks to a Feshbach resonance, experimentalists are not restricted to a single value of the scattering length, as they are in nuclear physics where it is given by nature. In ultracold gases, a control knob is available to precisely tune the interaction into desired regimes.

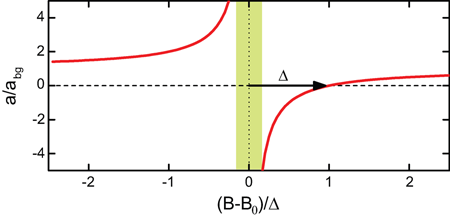
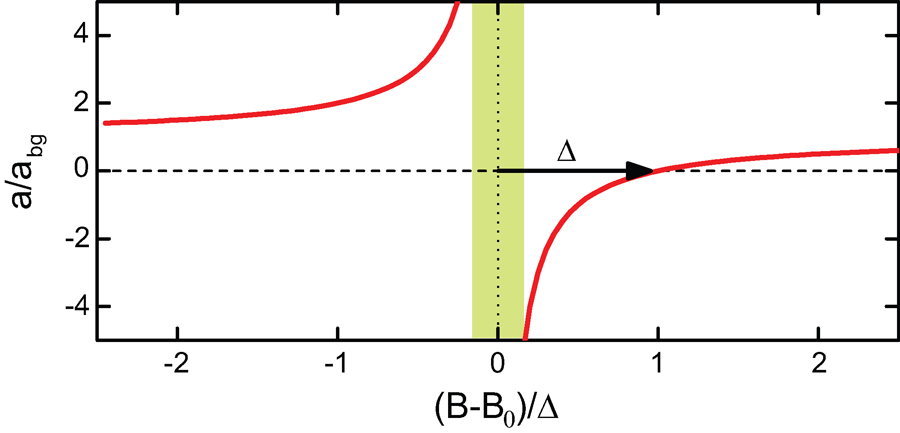
The physical origin of a Feshbach resonance is the coupling of the atomic scattering state to a bound molecular state when both states become degenerate [18]. The dependence on the magnetic field $B$, and thus the tunability, result from the different magnetic moments of the two states and leads to a typical behavior as shown in Fig. 2 and described by the expression

Here $B_0$ and $\mathrm{\Delta }$ denote the resonance position and width, respectively, and $a_{bg}$ is the so-called background scattering length. Near the resonance center, the inverse scattering length $1/a$ as used in Efimov’s scenario (Fig.1) is simply proportional to the magnetic detuning $B-B_0$. The parameters of Feshbach resonances can vary strongly, in particular depending on the properties of the atomic species. Resonances have been found in different systems with the width parameter $\mathrm{\Delta }$ ranging between a few milligauss and hundreds of gauss [18].

×

For an experimental realization of Efimov’s scenario near a Feshbach resonance, two conditions need to be fulfilled. Quite obviously, the scattering length must be large compared to the characteristic interaction range. For neutral atoms, the latter is determined by the van der Waals interaction and is typically found between $30a_0$ (for Li atoms) and $100a_0$ (Cs atoms), where $a_0$ is the Bohr radius. The second condition is more subtle and is intricately related to the physics of a Feshbach resonance [18]. Near the center of the resonance, a certain range exists where the two-channel interaction problem (scattering state and bound molecular state) simplifies and the situation can be treated like a single molecular interaction potential with a bound state very close to threshold. In this “universal” range, the physics is fully described by $a$ as a single parameter. The weakly bound dimer state for $a>0$ with an energy of $-{\mathrm{ħ}}^2/(m{a}^2)$ is a very important example for this universality.

Some resonances tend to have a universal range close to the width $\mathrm{\Delta }$. For other resonances, however, the universal range only extends over a very small fraction of the resonance width. Broad resonances with $|\mathrm{\Delta }|>>1$ gauss are usually resonances of the first kind and thus the best suited ones for probing Efimov physics.

Signatures of Efimov states can be found by measuring the decay of a trapped ultracold gas for a variable $s$-wave scattering length. An ideal environment for such measurements can be realized with optical dipole traps, in which atoms are held stationary with intense far-detuned laser light beams [19]. They allow for trapping of the atoms in the lowest internal atomic states, which means the trapping is immune against two-body losses by spin relaxation (as may occur in magnetic traps). Moreover, the optical traps allow for the application of arbitrary magnetic fields.

The leading decay process in such a trapped ultracold gas is three-body recombination, a process in which two atoms form a dimer and the binding energy is carried away by the recombination products, i.e., the dimer and an atom. This usually causes trap loss [13,20–22], providing the experimental observable in the experiments. The most striking signature for an Efimov state is the resonantly enhanced loss that occurs for $a<0$ at a so-called triatomic Efimov resonance [23]. Here three colliding atoms at the zero-energy threshold resonantly couple to an Efimov trimer (see arrow for $a<0$ in Fig. 1), which opens up a rapid decay path into more deeply bound dimer states.

Such a decay resonance was first observed in an ultracold trapped gas of cesium atoms [24]. The resonance is shown in the left-hand panel of Fig. 3. Temperatures as low as a few $10\text{nK}$ were necessary to observe the resonance with good contrast, as the recombination process is generally temperature-limited. This is demonstrated by further data taken at a “high” temperature of $\sim 200\text{nK}$.

×

On a historical note, the Stanford group was quite close to observing the Efimov resonance in the late 1990s; their data [14] indeed showed somewhat enhanced loss in the magnetic field region where the triatomic resonance occurs, but their $1\mu \text{K}$ sample was simply too hot to allow for a clear observation. Other loss features, later interpreted as Feshbach resonances involving higher partial waves, appeared much more prominently in the experiments and thus attracted the main attention. The Efimov resonance was then clearly seen in 2002 in (unpublished) experiments in Innsbruck en route to achieving Bose-Einstein condensation of cesium, but for over three more years it remained just an unidentified loss feature that did not attract attention.

An alternative possibility to observe an Efimov state is an atom-dimer resonance for $a>0$ [25]. Such a resonance was first identified with ultracold cesium in a mixture of atoms with weakly bound dimers [26]. The resonance shows up in the atom-dimer inelastic decay rate; see right-hand panel of Fig. 3. The basic reason is the same as for the triatomic resonance. The colliding particles resonantly couple to an Efimov state, opening up a path for rapid decay.

For atomic three-body decay, the loss recombination loss generally follows the rate equation

where $n$ denotes the atomic density and $L_3$ is the three-body loss coefficient. In the universal regime of large $a$, the coefficient $L_3$ can be written as

where the factor $n_l$ represents the number of atoms lost in a recombination event, which normally is three. The scattering length dependence can be separated into a general $a^4$ scaling [20,21] and a dimensionless function $C(a)$ [28]. The function $C(a)$ reveals the Efimov physics in the problem, following a logarithmically periodic dependence according to Efimov’s scaling law,

For the function $C(a)$, analytic expressions are available, based on effective field theory [28]. The experimental results can be fitted with the predictions of effective field theory, which involves two free parameters. Such fits are shown by the solid lines in Fig. 3. The two parameters are related to the resonance position and their width. The position is directly related to the (universal) three-body parameter, whereas the width corresponds to the lifetime of Efimov states against decay into more deeply bound states, which is beyond universal physics.

The cesium experiments in Innsbruck were the first to observe Efimov states by detecting the basic resonance phenomena for both negative and positive values of the scattering length. They also showed indications of a recombination minimum as another important feature related to universal three-body physics [22,29]. The tuning range in these cesium experiments, however, was restricted by the special properties of the low-field Feshbach resonance that was exploited. Therefore an important ingredient of Efimov physics, the existence of the universal scaling factor, remained unobserved.

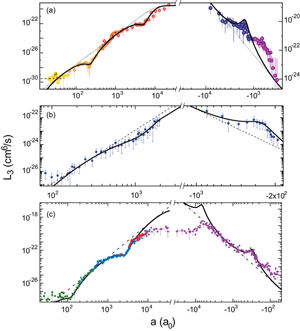
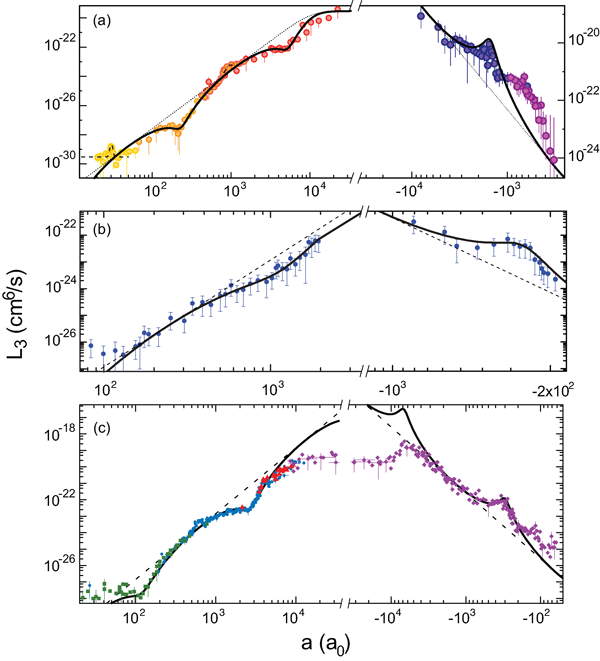
In 2009, three other groups reported experimental observations of Efimov states in bosonic quantum gases near a Feshbach resonance and provided further insight studying the decay properties near a Feshbach resonance. In these experiments, the complete tuning range across full Feshbach resonances could be exploited. The results of these experiments are compiled in Fig. 4.

×

The Florence experiment on ${}^{39}\text{K}$ [30] provided a first observation of Efimov’s scaling factor. Besides the observation of a triatomic resonance for $a<0$ similar to the cesium work, the major breakthrough of this work consisted of the observation of two consecutive minima in the three-body recombination rate for $a>0$. Such minima arise from the destructive interference between two recombination pathways [22], and they provide another signature of Efimov physics. The Florence group observed a ratio of $25\pm 4$ for the scattering lengths where the consecutive minima occurred. Within the experimental uncertainties, this value is consistent with Efimov’s scaling factor of $22.7$. A further prediction of universal theory is that these recombination minima should be located in between the positions of atom-dimer resonances. Surprisingly, although being performed with an atomic gas (and not an atom-molecule mixture), the Florence experiments also revealed signatures of these atom-dimer resonances. These observations took advantage of an avalanche effect caused when a dimer is formed in a three-body recombination event. At a resonance, the dimer has a large cross section for secondary collisions with atoms, which can lead to enhanced trap loss with $n_l>>3$ in Eq. (3).

The Bar Ilan group [31] and the Rice group [32] studied ultracold gases of ${}^7\text{Li}$. When comparing these two experiments, it is very interesting to note that they were performed on the same atomic system, but in two different internal states. The Bar Ilan group observed a triatomic resonance for $a<0$ along with a recombination minimum for $a>0$ and obtained a perfect fit of the overall behavior with universal theory. The Rice group observed many more features in the recombination spectrum. Similarly to the Florence group, they found two consecutive minima with a spacing close to Efimov’s factor of $22.7$, but their high-resolution data showed many more features such as atom-dimer resonance signatures and four-body resonances (see discussion later). All these observations were found to be in excellent agreement with universal theory, if one considers the $a<0$ and the $a>0$ regions separately. However, a universal connection for both signs of the scattering length could not be confirmed, in contrast to the Bar Ilan data.

These experiments could demonstrate all basic phenomena of Efimov’s original three-boson scenario, but they also raised questions in how far universal theories can be applied to quantitatively understand real-world systems and how they may be extended to near-universal regimes. We’ll come back to this important issue later, after looking into generalizations of Efimov’s scenario.

Efimov states not only exist for three identical bosons as we have discussed so far, but also in a variety of different other three-particle systems [28,33,34]. Distinguishable particles can be involved as well as particles of different masses, and under certain conditions even particle systems involving two identical fermions can exhibit Efimov states. These more general situations are of direct relevance for nuclear halo systems [8] such as a ${}^{18}\text{C}$ nucleus surrounded by two neutrons.

A remarkable system is an ultracold three-component Fermi gas of ${}^6\text{Li}$ atoms, where the population is equally distributed among the lowest three spin states. Such a system is generally characterized by three different scattering lengths. In the ${}^6\text{Li}$ gas, a wide magnetic-field region exists where overlapping Feshbach resonances lead to a situation where all three scattering lengths are very large. In this regime, the system is governed by universal physics and the existence of Efimov states can be expected.

Two groups, one in Heidelberg and the other one at Penn State University, have explored this system by measuring three-body decay [35–37]. While two-component Fermi mixtures at large scattering lengths are known to be extraordinarily stable, the three-component mixture can undergo very rapid decay. Here three-body collisions between distinguishable atoms can take place leading to the dominant loss mechanisms. The measurements showed three resonance features, which can be understood in terms of universal physics and interpreted as a result of Efimov trimer states intersecting the three-atom threshold [37–39].

The Efimov problem of distinguishable particles can be further generalized with particles of different masses [33,34]. Most strikingly, the mass ratio changes the geometric scaling factor and with extreme mass ratios it can be much smaller than the factor of $22.7$. This would lead to a much denser spectrum of Efimov states, so that a whole series of states might be observed in such systems. A first step into exploring Efimov physics in atomic species mixtures was reported by the Florence group on an ultracold Bose-Bose mixture of ${}^{87}\text{Rb}$ and ${}^{41}\text{K}$ atoms [40]. They observed both a three-body loss resonance attributed to $\text{K}-\text{K}-\text{Rb}$ collisions and another one related to $\text{K}-\text{Rb}-\text{Rb}$ collisions when they resonantly tuned the interaction across an interspecies Feshbach resonance. This experiment gives the first experimental evidence for the existence of the two expected families (light-light-heavy and light-heavy-heavy) of Efimov states in a system with mass imbalance.

How does the concept of universality extend to four bodies? How does the addition of a fourth particle modify the Efimov scenario? The existence of a universal class of three-body states is already surprising, but the concept of universal tetramer states is far beyond our imagination.

Three years after Efimov’s prediction, it was proven that no true Efimov effect exists for four or more identical particles [41]. Nevertheless, the question of possible universal four-body states remained open for many years [42–45], and no general consensus existed on what a true Efimov effect is. In the spirit of Ref. [41], the Efimov effect requires not only a precise scaling invariance but also well-defined thresholds, meaning that an $N-1$ bound state should cause the appearance of an infinite number of $N$-body bound states. Although this is not the case for $N>3$, other classes of universal four-body bound states could exist as a consequence of Efimov physics!

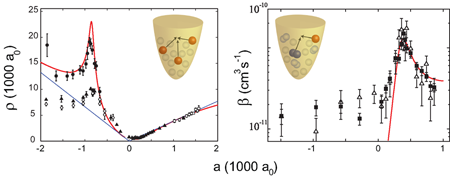
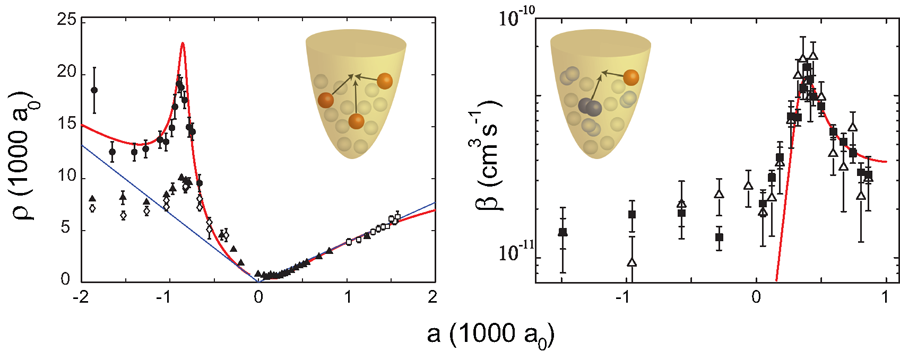
A fundamental step forward in understanding the four-body problem was recently made by two theory groups in Bonn/Ohio [46] and at JILA in Boulder [47]. They predicted that each Efimov state is accompanied by a pair of universal tetramer states. These states are genuinely related to Efimov physics since the four-body potential is attractive enough to support two universal tetramer states just in the proximity of a trimer state.

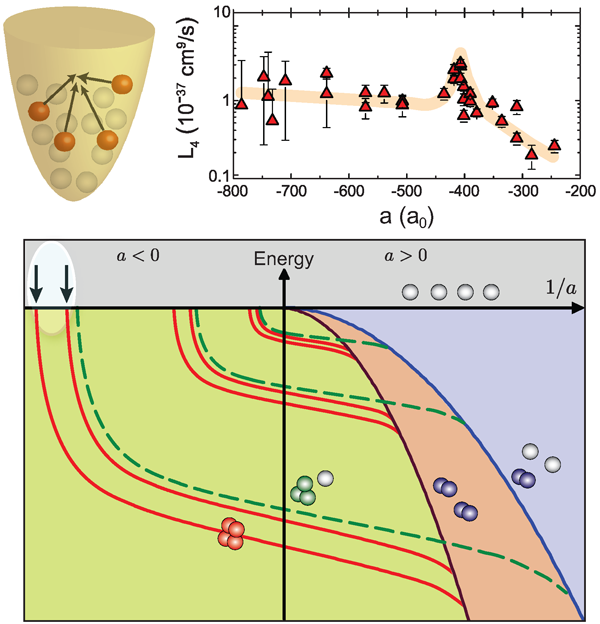
The JILA group found universal relations both in energy and in scattering length between the trimer state and the pair of tetramer states. The findings are in the spirit of the so-called Tjon lines explored in nuclear physics [48]. As shown in Fig. 5, these tetramer states emerge at the four-atom threshold and merge with the dimer-dimer threshold. At threshold, the presence of a tetramer state leads to a resonant change in the collisional behavior. In an ultracold gas, the manifestation would be resonantly enhanced four-body recombination. Such measurements were an unexplored terrain, and the fact that four-body processes could play a role in ultracold atomic samples and could be measured was surprising. Nevertheless, while reanalyzing the 2006 Innsbruck data on three-body recombination [24], the JILA group found possible indications of a four-body resonance [47]. Motivated by this result, the Innsbruck group rapidly started experiments specifically dedicated to four-body processes, and confirmed the central theoretical predictions [49]. The measurements clearly revealed the existence of a pair of four-body states tied to the previously detected Efimov trimer state [24] via the predicted universal relations. When a four-body resonance was approached, the atomic decay changed from a three-body behavior given by Eq. (2) to a four-body decay obeying the rate equation

where $L_4$ denotes is the four-body loss coefficient. The upper panel of Fig. 5 shows one of the four-body resonances. Similar results were then obtained in experiments on ${}^7\text{Li}$ atoms by the Rice group [32].

×

A further exciting step will be the study of the four-body spectrum in the region of positive scattering length, where resonant losses of dimers are expected because of the coupling to the tetramer states [50]. At the resonance positions, the Rice group observed enhanced atomic losses [32]. However, the underlying mechanism connecting the atomic decay features to resonant processes occurring at the dimer-dimer threshold is not fully understood and requires further investigations. A new generation of experiments on trapped dimer samples could clarify this issue and provide clear evidence of universal four-body states in molecular gases. First steps have been undertaken along this direction by studying scattering processes between ultracold halo dimers of cesium atoms [51,52].

The last year has shown a tremendous acceleration in progress on few-body physics with ultracold atoms. There are two major trends along which we see major developments in the field.

We thank all members of the Ultracold Atoms and Quantum Gases group in Innsbruck for many collaborations and inspirations. We particularly acknowledge the invaluable contributions of C. Chin, H.-C. Nägerl, S. Knoop, M. Mark, M. Berninger, A. Zenesini, and J. D’Incao to the work on Efimov physics in Innsbruck. We thank M. Zaccanti, L. Khaykovich, and R. Hulet for providing us with data for Fig. 4. We acknowledge support by the Austrian Science Fund (FWF) within SFB 15. F. F. was supported within the Lise Meitner program of the FWF.