The alphabet of spin in nanostructures

Rolf Allenspach; Philipp Eib

Viewpoint

The alphabet of spin in nanostructures

IBM Research–Zurich, Säumerstrasse 4, CH-8803 Rüschlikon, Switzerland

October 25, 2010• Physics 3, 91

A robust measurement scheme indicates that a spin-related torque that speeds up moving domain walls in magnetic nanostructures is larger than previously estimated.

Figure caption — **Figure 1:** Permalloy disk sample and contacts for current injection. (Top) Four $90$ ° domain walls intersect at the vortex core with its out-of-plane magnetization. (Bottom) As current flows through the disk, the vortex core is displaced due to the magnetic field of the current and due to spin-transfer torque. This displacement has been measured to quantify the nonadiabatic part of spin torque.

In a ferromagnetic nanostructure, a domain wall is a transition region that separates two different but uniformly magnetized regions. Moving a domain wall with an electrical current instead of a magnetic field is of great appeal to researchers; it could lead to spin-based devices in which information is stored and processed in domain walls. Such storage, memory, and logic devices could potentially be more flexible, efficient, and scalable.

The mechanism underlying this motion is called the spin-transfer torque, in which conduction electrons transfer a spin angular momentum to the local magnetization. The torque comes in an adiabatic and a so-called nonadiabatic part. There is much debate regarding the magnitude [1–5], microscopic origin [6–8], and even the existence [9] of the nonadiabatic term. In a paper in Physical Review Letters, Lutz Heyne and co-workers at the Universität Konstanz in Germany, along with collaborators in Switzerland, the US, and Germany [10], tell us how they measure the torque with a scheme [11] that involves displacing a single magnetic vortex by electrical current. They find a surprisingly large nonadiabaticity—favorable for spintronic devices based on domain walls—that not only dictates how quickly a domain wall moves but allows it to do so in the absence of applied magnetic fields, even for very small currents.

An intuitive phenomenological theory addresses the underlying physics. The Landau-Lifshitz-Gilbert (LLG) equation describes the evolution of magnetization in time: the magnetization vector precesses around any magnetic field that is present, eventually aligning with it as energy dissipates through dampening of the precession. In addition to the magnetization and the magnetic field, two quantities come into play: $γ$ , the gyromagnetic ratio that determines the frequency of precession, and $α$ , the parameter that describes the damping efficiency. As a spin-polarized current flows through a ferromagnet, the traveling spins tend to align with the magnetization. If the local magnetization direction changes, such as in a domain wall, angular momentum conservation requires the spins to exert a torque on the magnetization. This may result in domain-wall motion. This interaction is intricate, and two spin-transfer torque terms had to be incorporated into the LLG equation to describe it [6,12]. The first term is adiabatic: it describes the effect of spins as they move and adapt to locally varying magnetization. It is an “antidamping” term that is, like standard damping, proportional to $α$ , and contains no free spin-torque parameters. As noted in the paragraph above, the origin of the second term is unfortunately less clear. It has, for instance, been attributed to spin-flip scattering, which prevents the conduction electron spins from fully aligning with the magnetization [6] (hence dubbed “nonadiabatic”). This term introduces $β$ [12], the nonadiabaticity parameter, which is expected to be large for large magnetization gradients or narrow domain walls. The spintronics community is intrigued by both the absolute sizes as well as the ratio of these two terms, as illustrated by the large number of ongoing theoretical and experimental studies. These two terms determine the ease with which domain walls can be pushed along by current pulses.

There are numerous methods that measure $β$ from the motion of the domain wall. Even for a single material (permalloy) we are left with widely differing results: the majority of values for $β$ range from $0.01$ to $0.04$ , and for $β / α$ , from $1$ to $8$ . This could be due, at least in part, to the different experimental schemes employed to extract these values. Using vortex walls, i.e., walls with a curling magnetization pattern, Meier and coauthors measured the displacement of vortex core perpendicular to an applied current [2]. Moriya et al. applied alternating current to track the circling vortex core motion near a triangular notch [3]. Other approaches involved depinning a domain wall from either a local defect in the wire [1] or from an engineered notch [4]. Miron et al. determined $β$ in a perpendicularly magnetized material by compensating current effects with a magnetic field in dynamic equilibrium [5].

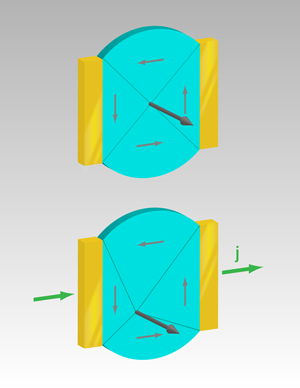
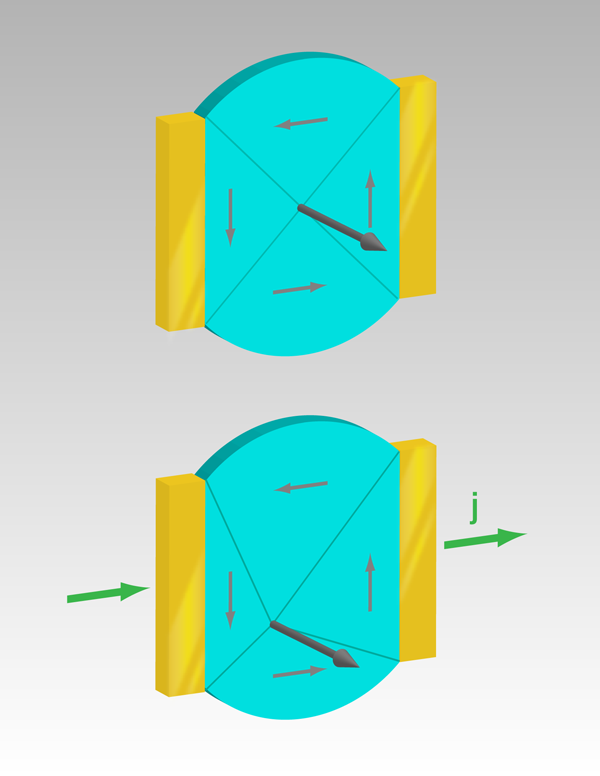
Heyne et al. [10] stepped into this arena with a measurement scheme proposed recently by Krüger et al. [11] that relies on determining the displacement of a magnetic vortex by electrical current. In materials with in-plane magnetization, these vortices are structures where the magnetization vector curls around a center core [13] and contain a significant out-of-plane magnetization component that minimizes the exchange energy (see Fig. 1, top). Typically, the vortices form in micrometer-sized soft magnetic elements, such as disks [10] or squares [11], and are characterized by two properties: the direction of rotation of the magnetization (the chirality) and whether the core magnetization points out of, or into, the plane (the polarity). As a current flows through a vortex, the core is displaced for three reasons: the magnetic field [14] accompanying the current, the adiabatic spin torque, and the nonadiabatic spin torque all push the core away from the center (Fig. 1, bottom). By measuring the core displacement and exploiting the different symmetries of the three contributions with respect to the direction of the current, vortex chirality, and polarity, it is possible to point to one contribution. In this way, we can gain insight into the character of the alphabet of the spin-transfer torque, and in particular into $β$ and $β / α$ .

The beauty of this method stems from the stability of the vortex structure as well as the simplicity of the three contributions to the vortex displacement. The sources of error are kept to a minimum as distances are measured, while keeping experimental parameters constant. The result is independent of the current density, the damping, or any structural imperfections at the edges. What is required, however, is an experimental method with high enough lateral resolution to accurately detect the location of the vortex core.

Employing x-ray magnetic circular dichroism in a photoemission electron microscope, Heyne et al. achieved this accuracy with a $6$ - $μ m$ -diameter permalloy disk into which they injected a large current density of up to $8 \times 10^{11} A / m^{2}$ . As the sample cannot withstand such a large current continuously, they injected short pulses of $25 μ s$ duration and let the sample cool down for $1 s$ before repeating the procedure. To capture the vortex core position in dynamic equilibrium, they imaged the core displacement only during current flow. To exploit the symmetry, they determined the displacement for both current directions and for two out of the four combinations of chirality and polarity. The analysis is delicate because, on the one hand, the magnetic field from the current produces a displacement that is larger than the one due to spin-transfer torque, while on the other hand, pinning sites in the disk—observed already earlier by the same group [15]—may preclude a displacement of vortex cores upon current changes. Despite these obstacles, the authors were able to extract $β$ from their data, because the angle between the displacement and the current direction is directly proportional to $β$ [11]. The proportionality factor contains the gyromagnetic properties of the vortex and its energy dissipation and was determined by micromagnetic simulations. The final result is $β = 0.15 \pm 0.07$ , translating to $β / α \approx 19$ , which suggests an unexpectedly large influence of the nonadiabatic spin torque on current-induced domain-wall motion.

Even with this elegant scheme to extract $β$ , many open fundamental questions remain. As explained above, nonadiabaticity should depend on the domain-wall width. However, Burrowes et al. found no significant dependence of $β$ on the domain-wall width for nanometer-wide walls in a perpendicularly magnetized material [16]. This might hint at a universal source for the nonadiabatic term, in the sense that the separation into two torque contributions is artificial and $β = α$ strictly holds. Damping by spin waves [8] could be a reason for this equality. Spin-transfer torque studies on domain walls are most commonly done in wires that are only some hundreds of nanometers wide because for small structures the influence of the magnetic field of the current is reduced. Such a small geometry, however, leads to increased temperature effects, which are hard to separate, especially in domain-wall depinning measurements. After all, $β$ might be temperature-dependent. Thus research on spin-transfer torque and current-driven wall motion remains an ongoing part of domain-wall physics, as it constitutes a fascinating combination of spin-dependent itinerant electron transport and nonlinear magnetization dynamics. The present work has helped to decrease our illiteracy of the spin-torque alphabet. It remains to be seen whether large nonadiabaticities also exist in other geometries and materials. We are convinced that the first letters of the spin-torque alphabet, in particular $β$ , need—and will receive—further attention. After all, the understanding of nonadiabaticity is crucial for exploiting spin-transfer torque in any future domain-wall devices.

References

L. Thomas, M. Hayashi, X, Jiang, R. Moriya, C. Rettner, and S. S. P. Parkin, Nature 443, 197 (2006)
G. Meier, M. Bolte, R. Eiselt, B. Krüger, D.-H. Kim, and P. Fischer, Phys. Rev. Lett. 98, 187202 (2007)
R. Moriya, L. Thomas, M. Hayashi, Y. B. Bazaliy, C. Rettner, and S. S. P. Parkin, Nature Phys. 4, 368 (2008)
S. Lepadatu, A. Vanhaverbeke, D. Atkinson, R. Allenspach, and C. H. Marrows, Phys. Rev. Lett. 102, 127203 (2009)
M. Miron, P.-J. Zermatten, G. Gaudin, S. Auffret, B. Rodmacq, and A. Schuhl, Phys. Rev. Lett. 102, 137202 (2009)
S. Zhang and Z. Li, Phys. Rev. Lett. 93, 127204 (2004)
I. Garate, K. Gilmore, M. D. Stiles, and A. H. MacDonald, Phys. Rev. B 79, 104416 (2009)
Y. Le Maho, J.-V. Kim, and G. Tatara, Phys. Rev. B 79, 174404 (2009)
S. E. Barnes and S. Maekawa, Phys. Rev. Lett. 95, 107204 (2005)
L. Heyne, J. Rhensius, D. Ilgaz, A. Bisig, U. Rüdiger, M. Kläui, L. Joly, F. Nolting, L. J. Heyderman, J. U. Thiele, and F. Kronast, Phys. Rev. Lett. 105, 187203 (2010)
B. Krüger, M. Najafi, S. Bohlens, R. Frömter, D. P. F. Möller, and D. Pfannkuche, Phys. Rev. Lett. 104, 077201 (2010)
A. Thiaville, Y. Nakatani, J. Miltat, and Y. Suzuki, Europhys. Lett. 69, 990 (2005)
T. Shinjo, T.Okuno, R.Hassdorf, K.Shigeto, and T. Ono, Science 289, 930 (2000)
S.-B. Choe, Y. Acremann, A. Scholl, A. Bauer, A. Doran, J. Stöhr, and H. A. Padmore, Science 304, 420 (2004)
L. Heyne, M. Kläui, D. Backes, T. A. Moore, S. Krzyk, U. Rüdiger, L. J. Heyderman, A. Fraile Rodríguez, F. Nolting, T. O. Mentes, M. Á. Niño, A. Locatelli, K. Kirsch, and R. Mattheis, Phys. Rev. Lett. 100, 066603 (2008)
C. Burrowes, A. P. Mihai, D. Ravelosona, J.-V. Kim, C. Chappert, L. Vila, A. Marty, Y. Samson, F. Garcia-Sanchez, L. D. Buda-Prejbeanu, I. Tudosa, E. E. Fullerton, and J.-P. Attané, Nature Phys. 6, 17 (2010)

About the Authors

Rolf Allenspach leads the Physics of Nanoscale Systems group at the IBM Research Laboratory in Rüschlikon, Switzerland. He received his Ph.D. from the ETH Zurich in 1986 for his work in the field of spin-polarized electron spectroscopy. His research at IBM focuses on nanomagnetism and, in particular, high-resolution imaging of magnetic patterns. He also enjoys lecturing at ETH on topics of condensed matter physics since completing his Habilitation in 1994.

Philipp Eib received his master’s degree in physics from the ETH Zurich. He is currently pursuing his doctorate at the IBM Research Laboratory in Rüschlikon, Switzerland. He uses spin-resolved scanning electron microscopy and time-resolved Kerr microscopy to study nanomagnetism, with emphasis on the statics and dynamics of magnetic domain walls.