Exotic many-body physics with large-spin Fermi gases

Congjun Wu

Viewpoint

Exotic many-body physics with large-spin Fermi gases

Department of Physics, University of California, San Diego, CA 92093, USA

November 1, 2010• Physics 3, 92

The experimental realization of quantum degenerate cold Fermi gases with large hyperfine spins opens up a new opportunity for exotic many-body physics.

Figure caption — **Figure 1:** (a) In solid-state systems with large total spin on each site, spin fluctuations occur by super exchange, where, at the leading order, one spin-up is exchanged for a spin-down electron. The size of the fluctuations of $S_{z}$ can only be $\pm 1$ in a total spin of $S$ , so the fluctuations are relatively small at large $S$ . (b) In cold-atom Fermi systems with large hyperfine spin, the atom moves as an entire object. In this case, the fluctuations of $S_{z}$ can be a much larger value of $\pm S$ .

Cold atom physics has become a new frontier, both for the study of known condensed matter phenomena such as superfluid-Mott insulator transitions, and as a way of creating novel quantum phases. Many atoms have large spins and can be stored and investigated in optical traps and lattices. Thus recent experimental progress on the large-spin ultracold Fermi gases provides an exciting opportunity to investigate exotic many-body physics, as reported in two recent articles published in Physical Review Letters. In one case, Desalvo et al. [1] have cooled down the system of $^{87} Sr (F = I = 9 / 2$ , where I is the nuclear spin and F is the total hyperfine spin) to quantum degeneracy (that is, a situation where the atoms occupy the lowest possible energy states limited by Pauli exclusion). Now, Shintaro Taie and colleagues at Kyoto University, Japan, and the Japan Science and Technology Agency report their success in cooling of $^{173} Yb (F = I = 5 / 2$ ) [2]. Both $^{87} Sr$ and $^{173} Yb$ have an alkaline-earth-like atomic structure with all electron shells filled; thus their hyperfine spins completely come from nuclear spins. Since nuclei are deep within the atom, interactions among atoms are nearly spin-independent. As a result, we now have the opportunity to explore, in an atomic system, complex many-body physics of the sort usually only seen in high-energy physics.

For these atomic systems, all the $2 F + 1$ hyperfine levels are equivalent in terms of their participation in atom-atom interactions, which gives rise to the so-called SU(N) symmetry, with $N = 2 F + 1$ , in the language of symmetry groups. Mathematicians and physicists know SU(N) as the special unitary group of degree N, which can be represented by a set of $N \times N$ unitary matrices with determinant $1$ . The purpose of such groups is to capture the symmetry properties that govern the behavior of various particles. The matrices transform a vector (representing a particle or state) in an abstract N-dimensional space into another vector (or particle). $SU (2)$ , for example, appears in the physics of spin- $1 / 2$ particles like electrons, which can be spin up or spin down. The $SU (3)$ group is found in quantum chromodynamics—the physical theory of quarks and gluons—in which there are three particle “colors.” Higher dimensional groups, such as $SU (N)$ , where $N = 2 F + 1$ , could then represent particles of hyperfine spin F. For instance, $^{173} Yb$ with spin = $5 / 2$ has six components with $F_{z}$ equal to $- 5 / 2, - 3 / 2, - 1 / 2, + 1 / 2, + 3 / 2$ , and $+ 5 / 2$ , requiring an $SU (6)$ symmetry group. Taie et al. have gone further, however, loading the $^{173} Yb$ atoms into three-dimensional optical lattices together with atoms of its spin $- 1 / 2$ isotope, $^{173} Yb$ . This mixture of spin species is then a realization of an $SU (6) \times SU (2)$ system [2], where the direct product symbol $\times$ means that the symmetry transformation in one isotope sector is independent of that in the other.

In general, cold Fermi systems with large hyperfine spins have aroused a great deal of theoretical interest. Researchers have studied the rich structure of collective excitations in Fermi liquid theory [3] and the Cooper pairing patterns of large spin fermions [4]. Considerable progress has been made in the simplest large-hyperfine-spin systems with $F = 3 / 2$ (e.g., $^{132} Cs,^{9} Be,^{135} Ba,^{137} Ba,^{201} Hg$ ) [5,6], which also include non-alkaline-earth atoms with nonzero electron spins due to partially filled electron shells. In this case, the $SU (N)$ symmetry is not generic. Instead, a hidden $SO (N)$ symmetry with $N = 5$ is proved without fine tuning, where $SO (N)$ is the special orthogonal group describing rotations in an N-dimensional real space. Important effects from such as symmetry on quantum magnetism and Cooper pairing have been studied [7–9]. Recently, $SU (N)$ models have been proposed for the alkaline-earth fermion atoms, whose effects on quantum magnetism have been explored based on the field-theoretical method of large N [10,11]. The possible ferromagnetic states have also been studied for the $SU (6)$ symmetric system of $^{173} Yb$ [12].

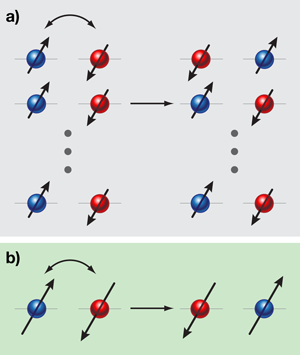
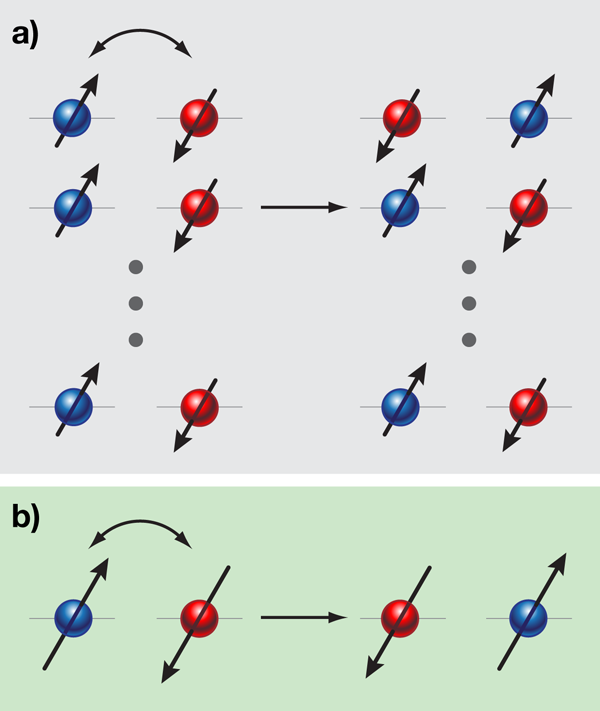
Why are such large-spin Fermionic cold-atom systems so important? The reason is the fundamental difference between large-hyperfine-spin Fermi systems and large-electron-spin solid-state systems. For example, in many transition-metal oxides, several electrons on the same cation site combine into a composite object with a large electron spin $S > 1 / 2$ through Hund’s rule coupling. (In chemistry, Hund’s rule refers to the situation when electron shells are partially filled and the total spin of unpaired electrons adds together.) Usually, however, large spins are not particularly interesting compared to spin $1 / 2$ , because quantum spin fluctuations become weaker for large spins in electron systems. This point is intuitively illustrated in Fig. 1 (a). The intersite coupling between large electron spins is dominated by the exchange of a single pair of electrons. The change of $S_{z}$ can only be $\pm 1$ , regardless of the value of S, thus spin fluctuations are on the order of $1 / S$ . As a result, the larger the electron spins are, the more classical is the physics they exhibit.

In contrast, such a restriction does not exist in cold Fermi systems with large hyperfine spins. Each atom moves as a whole object carrying a large hyperfine spin, as depicted in Fig. 1 (b). Exchanging cold fermions can completely flip the total hyperfine-spin configuration. Consequentially, as pointed out in Ref. [6], quantum fluctuations are enhanced by the large number of hyperfine-spin components N, which are even stronger compared to those in spin-1/2 systems. In other words, large-hyperfine-spin cold-atom systems can exist in the large-N limit. This feature gives rise to the possibilities of realizing exotic quantum magnetic states [7,10,11], including various spin liquids and valence-bond solid states that are difficult to stabilize in electron systems.

Large-hyperfine-spin cold fermions also bring nontrivial features to the Cooper pairing found in superfluidity. In conventional spin- $1 / 2$ systems, the only possibility for the s-wave pairing is that of spin singlet, that is, a spin-up paired with a spin-down fermion, with the total spin zero. In the large-hyperfine-spin case, the s-wave Cooper pair can take even values of the total hyperfine spin, ranging from $0, 2$ to $2 S - 1$ [4]. This results in interesting spin dynamics of pairing condensates, and exotic topological defects with combined vortices in the phase and spin configurations of the pairing condensate [4,9].

Another exotic physical phenomenon in large-hyperfine-spin cold fermions is the “baryonlike” multiple-fermion clustering instability. In an N-component Fermi system with attractive interactions, Pauli’s exclusion principle allows, at most, N fermions to form an $SU (N)$ singlet state [13,7]. Compared to Cooper pairing, such a state has a lower interaction energy but costs more kinetic energy, thus is favored when interactions are strong. In quantum chromodynamics (QCD), baryons, which are color singlets, are composed of three quarks because two quarks cannot form a color singlet for the $SU (3)$ color gauge group. It is interesting that in spite of the huge difference of energy scales, the large-spin cold fermions can also exhibit similar physics to that in QCD [14].

The exploration of many-body physics with large-spin ultracold fermions is a promising research direction of cold-atom physics. A major experimental challenge is the precise control of interactions among atoms, which is important to realize exotic Cooper pairing with rich internal spin structure. To experimentally study exotic quantum magnetism with large-spin fermions, further cooling the temperatures below the magnetic exchange energy scale is necessary. It is natural to expect that this research will greatly expand our knowledge of many-body physics different from that in electron systems.

References

B. J. DeSalvo, M. Yan, P. G. Mickelson, Y. N. Martinez de Escobar, and T. C. Killian, Phys. Rev. Lett. 105, 030402 (2010)
S. Taie, Y. Takasu, S. Sugawa, R. Yamazaki, T. Tsujimoto, R. Murakami, and Y. Takahashi, Phys. Rev. Lett. 105, 190401 (2010)
S. K. Yip and T. L. Ho, Phys. Rev. A 59, 4653 (1999)
T. L. Ho and S. K. Yip, Phys. Rev. Lett. 82, 247 (1999)
C. Wu, J. P. Hu, and S. C. Zhang, Phys. Rev. Lett. 91, 186402 (2003)
C. Wu, Mod. Phys. Lett. B 20, 1707 (2006)
C. Wu, Phys. Rev. Lett. 95, 266404 (2005); S. Chen, C. Wu, S. C. Zhang, and Y. P. Wang, Phys. Rev. B 72, 214428 (2005); C. K. Xu and C. Wu, 77, 134449 (2008)
D. Controzzi and A. M. Tsvelik, Phys. Rev. Lett. 96, 097205 (2006); S. Capponi, G. Roux, P. Azaria, E. Boulat, and P. Lecheminant, Phys. Rev. B 75, 100503 (2007); H. H. Tu, Guang-Ming Zhang, and Lu Yu, 76, 014438 (2007)
C. Wu, J. P. Hu, and S. C. Zhang, Int. J. Mod. Phys. B 24, 311 (2010)
A. V. Gorshkov, M. Hermele, V. Gurarie, C. Xu, P. S. Julienne, J. Ye, P. Zoller, E. Demler, M. D. Lukin, and A. M. Rey, Nature Phys. 6, 289 (2010)
M. Hermele, V. Gurarie, and A. M. Rey, Phys. Rev. Lett. 103, 135301 (2009); C. K. Xu, Phys. Rev. B 81, 144431 (2010)
M. A. Cazalilla, A. F. Ho, and M. Ueda, New J. Phys. 11, 103033 (2009)
P. Lecheminant, P. Azaria, and E. Boulat, Nucl. Phys. B 798, 443 (2008); P. Lecheminant, E. Boulat, and P. Azaria, Phys. Rev. Lett. 95, 240402 (2005); D. Lee, 98, 182501 (2007)
A. Rapp. G. Zarand, C. Honerkamp, and W. Hofstetter, Phys. Rev. Lett. 98, 160405 (2007)

About the Author

Congjun Wu received his Ph.D. in physics from Stanford University in 2005, and did his postdoctoral research at the Kavli Institute for Theoretical Physics, University of California, Santa Barbara, from 2005 to 2007. He became an assistant professor in the Department of Physics at the University of California, San Diego, in 2007. His research interests include quantum magnetism, superconductivity, orbital physics, and topological states in condensed-matter and cold-atom systems.