Meet a superpartner at the LHC
Of the many ideas for new physics that can be tested at the Large Hadron Collider (LHC), supersymmetry is one of the most promising. The theory proposes that each fundamental fermion particle has a heavier bosonic superpartner (and vice versa for each fundamental boson) and by doing so, offers an extension of the standard model of particle physics that fixes many of its problems. None of the known particles appear to be superpartners, however, which leads to the daunting conclusion that if supersymmetry is correct, there are more than twice as many fundamental particles as we thought, but we have only been left with the lightest partners; that is, supersymmetry is broken.
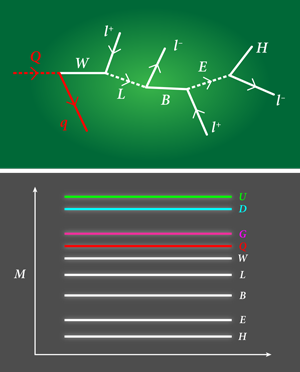
The large number of unknown superpartner masses has made it difficult for theorists to guide experiments in the search for supersymmetry breaking, but a theoretical paper appearing in Physical Review Letters by Partha Konar and colleagues at the University of Florida in the US attempts to simplify the problem in a way that is most useful to experimentalists [1]. They identify the 9!=362,880 ways that the superpartner masses can be arranged from heaviest to lightest and discuss the experimentally observable features of certain “classes” of ranked masses (Fig. 1). Konar et al. point to the small, but non-negligible number of these supersymmetry breaking patterns that should have dramatic signatures in the decay chains that follow high-energy particle collisions.
In the last 40 years, particle physicists have developed the spectacularly successful “standard model” of the strong, weak, and electromagnetic interactions. The standard model is a mathematically consistent field theory. Most aspects have been stringently tested, and it is almost certainly the approximately correct description of nature, down to a distance scale 1/1000th the size of the atomic nucleus. Nevertheless, few physicists believe that the standard model is the final story. The model doesn’t explain some of the most fundamental observations of modern physics, including why the particles that carry and interact via the electroweak force have mass, the presence of dark matter and dark energy in the universe, and the excess of matter over antimatter. Nor does the standard model incorporate a quantum theory of gravity. A final issue is one of aesthetics: the standard model is arbitrary and complicated, and contains many parameters that are either free (such as the masses of the quarks and leptons) and have to be experimentally determined, or require fine-tuning (the value of the energy of the vacuum, which is infinitesimally small on particle physics scales, is one example). The model also has the unexplained feature that it predicts the existence of two heavier versions of the electron (the tau and the muon) and the quarks that make up nucleons (namely the charm, strange, top, and bottom quarks). Most of the experimental and theoretical activity in high-energy particle physics is therefore either directed towards understanding the masses of the electroweak particles (e.g., the search for the Higgs particle) or searching for an even more fundamental underlying theory to address the shortcomings of the standard model.
Supersymmetry is one extension of the standard model that is especially promising. The theory has a number of advantages that compensate for the fact that it introduces more than double the number of fundamental particles. To start with, supersymmetry is, under reasonable assumptions, the unique extension of the Lorentz and translational symmetries of spacetime in a local field theory. In addition, while the standard model introduces large “radiative corrections,” which tend to wash out the enormous difference (“hierarchy”) in energies associated with the electroweak force and Planck (gravity) scales, supersymmetry cancels out these corrections and is therefore said to “protect” the hierarchy of energies. The new supersymmetric particles allow a simple unification of the strengths of the strong, weak, and electromagnetic interactions when they are extrapolated to high energies. No less important is that most versions of supersymmetry involve new particles that could be the particles that constitute the cosmological dark matter. Finally, supersymmetry allows a possible connection to quantum gravity through superstring theory.
Experimental constraints suggest that the masses of most of the superpartner particles would have to exceed hundreds of GeV, but they are not likely to be too much higher than a few TeV if supersymmetry protects the electroweak scale. This window of energies is well within reach of the LHC. To maintain the desirable features of the theory, supersymmetry breaking has to occur in ways that we can’t directly observe; i.e., the dynamics of supersymmetry breaking must occur in some “hidden” sector of nature that communicates with ordinary particles via a very weak interaction. (This often occurs when the supersymmetry emerges from an underlying superstring theory.) Concrete examples for the communication have been discussed in the context of gravity (supergravity) or standard model interactions of some new very heavy particles (gauge mediation). For a review, see Ref. [2].
There are many possible theories of supersymmetry breaking and a general study of the consequences would involve of order 100 free parameters. Therefore, almost all studies have focused on specific models for supersymmetry breaking (and the way this symmetry breaking gets communicated to ordinary particles), usually with additional simplifying assumptions to limit the number of parameters. A small number of “benchmark” examples have been examined most carefully. These studies have been very useful for getting a general idea of typical experimental signatures of supersymmetry, setting limits for representative cases, and devising search strategies for experiments at the LHC and the Tevatron, as well as dark matter searches. However, they do not represent all of the possibilities, and it is possible that the actual spectrum of superpartners differs qualitatively from the examples.
Several recent papers [3–6] have taken a more theory-“unprejudiced” point of view, and have studied large numbers of possible supersymmetry breaking parameters and their implications, generally by scanning over parameter space and applying existing experimental constraints (such as the absence of certain decays). Konar et al. take a somewhat different and very intuitive approach. They categorize each pattern of supersymmetry breaking by nine superpartner mass parameters, corresponding to the partners of the gluons (G), weak interaction bosons (W and B), left-handed quark (Q) and lepton (L) doublets, right-handed quarks and leptons (U, D, E), and Higgs particles (H). For simplicity, it is assumed that the first two families of lepton and quark partners of each type are degenerate, which suppresses problems with rare decays, and the third family (the tau lepton and the top and bottom quarks) is ignored. The characteristics of the 9! hierarchies or orderings of these masses are discussed, especially the 161,280 cases in which the lightest (L,B,W,H) can be electrically neutral, leading to unobserved (missing) energy in events measured at the LHC and a dark matter candidate (assuming it is stable). These are further classified according to the position of the lightest colored particle (G,Q,U,D) in the hierarchy, since these should be strongly produced in pairs at the LHC. For each such ordering, the group analyzes the dominant decay chains according to the number of quark jets, leptons, and massive electroweak or Higgs bosons that should be observed in experiments. Most of the hierarchies they obtain lead to dominant decay chains similar to those in most of the familiar (e.g., supergravity) models, typically involving multiple jets, missing energy, and small numbers (or none) of leptons and massive vectors. However, a non-negligible number (a fraction of a percent) may involve signals such as eight isolated leptons, two jets, and missing energy. Such events would be spectacular in that they would be easy to observe and there are essentially no standard model backgrounds. It is these examples that Konar et al. study in greatest detail (Fig. 1).
There are many other signatures of supersymmetry that Konar et al. do not explicitly discuss. One is the possibility of finding a light gravitino (the superpartner of the graviton) in the decays of high-energy particles. Other possible signatures include decays involving the third family of the electron and the quark (namely, the tau and top and bottom quarks), or the existence of a light, right-handed neutrino (predicted by some theories that explain the small but nonzero neutrino masses) and its superpartner. Finally, there is the possibility that none of the supersymmetric partners are actually stable (R-parity breaking), which would imply that the dark matter has a different origin. The “unprejudiced” theoretical studies in Konar et al.’s work and other papers illustrate the rich range of possible signatures of supersymmetry that should be observable at the LHC and elsewhere.
References
- P. Konar, K. T. Matchev, M. Park, and G. K. Sarangi, Phys. Rev. Lett. 105, 221801 (2010)
- D. J. H. Chung, L. L. Everett, G. L. Kane, S. F. King, J. D. Lykken, and L. T. Wang, Phys. Rep. 407, 1 (2005)
- D. Feldman, Z. Liu, and P. Nath, Phys. Rev. Lett. 99, 251802 (2007); 100, 069902(E) (2008)
- C. F. Berger, J. S. Gainer, J. L. Hewett, and T. G. Rizzo, J. High Energy Phys. 2009, No. 02, 023 (2009)
- C. Horn, J. Phys. G 36, 105005 (2009)
- J. A. Conley, J. S. Gainer, J. L. Hewett, M. P. Le, and T. G. Rizzo, arXiv:1009.2539 (hep-ph)