Tuning Correlations in a 2D Electron Liquid

Johann Kroha

Viewpoint

Tuning Correlations in a 2D Electron Liquid

Physikalisches Institut and Bethe Center for Theoretical Physics, Universität Bonn, Nussallee, 12, D-53115 Bonn, Germany

December 12, 2011• Physics 4, 106

Simulating part of a perovskite heterostructure with a polarizable gel reveals the instrinsic properties of a two-dimensional electron liquid.

Figure caption — **Figure 1:** (a) Lattice structure of the $STO$ - $LAO$ interface, showing the unpoled $SrO$ and ${TiO}_{2}$ planes in $STO$ as well as the ${LaO}^{+}$ and ${AlO}_{2}^{-}$ planes with alternating polarity in $LAO$ . (b) Simulation of the $LAO$ overlayer by an electrolytic gel with frozen-in polarization, allowing for controlled tuning of the charge-carrier density in the two-dimensional electron gas. The diagrams to the right of (a) and (b) show the potential energy of the $LAO$ overlayer and of the polarized gel, respectively, increasing linearly with layer thickness.

Undoped strontium titanate, ${SrTiO}_{3}$ (STO), is a widely studied ceramic material with a huge dielectric constant $ε$ , ranging from $300$ at room temperature up to $5000$ at $T = 80 K$ [1]. The large values of $ε$ are a macroscopic signature that the internal charges are easily displaced by an external electric field, while the material remains an excellent insulator. These properties have made STO an interesting material for high-performance capacitors [2]. More fundamentally, this apparently paradoxical behavior is an indication that our conventional picture—of single electrons determining the dielectric properties—fails here, and strong electronic correlations play an important role. Bearing STO’s strongly insulating behavior in mind, it was a big surprise when it was discovered that, at the interface of the two insulators ${SrTiO}_{3}$ and ${LaAlO}_{3}$ (LAO), there exists a two-dimensional electron liquid (2DEL) with high mobility of the electrons parallel to the interface [3]. Later findings that this electron liquid can have magnetic order [4], superconduct [5], and even exhibit a coexistence of these two phases [6,7] raised even more excitement (see also 25 July 2011 Viewpoint).

However, it is still uncertain how the electronic structure of the STO layers changes in response to the LAO layers, for instance, whether oxygen vacancies or cation intermixing between the lanthanum and strontium is responsible for the creation of the 2DEL observed at the interface. Now, a new approach to “simulate” the LAO layers without introducing additional defects is reported in Physical Review Letters by Menyoung Lee at Stanford University, California, and collaborators [8]. They have replicated the STO/LAO interface by replacing the polar LAO with a polarizable gel. In this way, they have been able to continuously tune the electron density, the crucial parameter of the 2DEL, gaining significant new insight into the nature of the charge carriers.

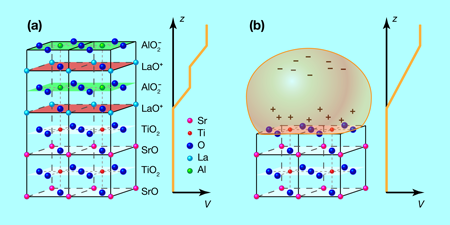
Both STO and LAO are layered materials of the so-called perovskite crystal structure with strongly ionic bonding. STO consists of alternating layers of $SrO$ and ${TiO}_{2}$ [Fig. 1(a), bottom]. The ions reach their stable closed-shell configuration with the nominal charges ${Sr}^{2 +}$ , ${Ti}^{4 +}$ , and $O^{2 -}$ , respectively, so that each of the two types of layers are overall uncharged. In $LAO$ , the ${Sr}^{2 +}$ ions are replaced by ${La}^{3 +}$ , and the ${Ti}^{4 +}$ ions by ${Al}^{3 +}$ [Fig. 1(a), top]. Hence, the $LaO$ and ${AlO}_{2}$ layers carry alternating charges $+ 1$ and $- 1$ per unit cell, respectively. The pairwise stacking of these layers in $LAO$ induces surface charges and causes the potential energy of the arrangement to increase linearly with the number of layers, analogous to shunting charged capacitors in series. It is believed that at an STO/LAO interface terminated by a ${TiO}_{2}$ layer [see Fig. 1(a)], the STO responds to this so-called polarization catastrophe by accumulating electrons near the interface, partially compensating the positive LAO surface charge. These additional electrons reach a critical density to become conducting when the LAO exceeds a thickness of three double layers [9].

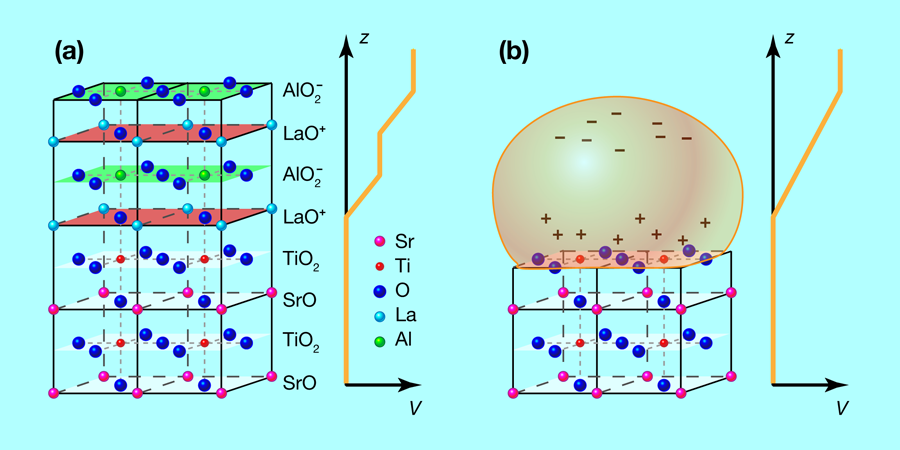
Although Lee et al.’s attempt is not the first to induce a 2DEL in STO without LAO, their method enables them to have significantly better control over the interface quality than previous electrostatic doping techniques [10,11]. Lee et al. have replaced the LAO with an electrolytic gel consisting of a salt dissolved in a polymer [see (Fig. 1(b)]. They first polarized the gel at room temperature with a voltage applied perpendicular to the interface, then cooled their sample down to the measurement temperature (a minimum of $T = 1.4 K$ ), where the gel and its polarization are frozen. They performed their measurements after switching off the voltage. The density of mobile charge carriers was determined in a standard way by measuring the Hall coefficient of the 2DEL, which is inversely proportional to the mobile carrier density, $R_{H} = - 1 / n e$ , where $e$ is the carrier charge and $n$ the carrier number density. The measurements show that a mobile charge-carrier density $n$ is indeed induced by a polarized overlayer and resides on the STO side of the interface, as expected [9]. The carrier number density can be tuned in a wide range by the initially applied polarizing voltage. Thus the electrolytic polarization freezing method provides a realistic simulation of the polar interface.

The use of the gel enables Lee et al. to make some surprising discoveries about the 2DEL. The main experimental results pertain to the longitudinal electrical resistance $R$ . The measurements in zero magnetic field show a minimum of $R$ as a function of temperature $T$ , which becomes more pronounced and shifted towards higher temperatures with increasing carrier density (see Figs. 2 and 3 in Ref. [8]). While the increase of $R$ towards high temperatures is expected from scattering by thermal excitations, the resistivity upturn and saturation towards low temperatures is a typical signature of the Kondo effect [11], arising from the scattering of conduction electrons from localized magnetic spins. The experimental observation of this complex low-temperature behavior is a strong indication that, in the 2DEL of STO, there are both localized spins and itinerant electrons interacting with each other, leading to a Kondo effect.

Though weak or strong localization due to disorder could mimic the Kondo signatures, the authors ruled this out by measurements in magnetic fields that allow the differentiation between Kondo and localization effects in the resistance behavior. Another possibility is that the local magnetic moments in the nominally nonmagnetic $STO$ might be due to unintentional contamination with magnetic ions, like iron. Lee et al. excluded this possibility by measuring the dependence of the low-temperature resistance on the carrier concentration. The local moment concentration increases with the concentration of itinerant charge carriers $n$ and thus must be intrinsic to the 2DEL itself.

Thus, by performing a detailed analysis on the dependence of resistance on temperature, magnetic field, and carrier density, Lee et al. have obtained evidence that there is intrinsically an interaction between local and itinerant magnetic moments, leading to a Kondo effect. In particular, tuning the charge-carrier concentration in a controlled way by a frozen-in polarization of an electrolytic overlayer has been instrumental for reaching this conclusion. This method may well become a versatile tool for investigating interfaces of strongly correlated insulators to ferroelectrics. The remarkable results are bound to stimulate further experimental and theoretical work to confirm and understand this coexistence of intrinsic local and itinerant magnetic moments in the two-dimensional electron liquid at the STO/LAO interface.

References

D. Fuchs, C. W. Schneider, R. Schneider, and H. Rietschel, J. Appl. Phys. 85, 7362 (1999)
L. Li, C. Richter, S. Paetel, T. Kopp, J. Mannhart, and R. C. Ashoori, Science 332, 825 (2011)
A. Ohmoto and H. Y. Hwan, Nature 427, 423 (2004)
A. Brinkman, M. Huijben, M. van Zalk, J. Huijben, U. Zeitler, J. C. Maan, W. G. van der Wiel, G. Rijnders, D. H. A. Blank, and H. Hilgenkamp, Nature Mat. 6, 493 (2007)
N. Reyren, S. Thiel, A. D. Caviglia, L. Fitting Kourkoutis, G. Hammerl, C. Richter, C. W. Schneider, T. Kopp, A.-S. Ruetschi, D. Jaccard, M. Gabay, D. A. Muller, J.-M. Triscone, and J. Mannhart, Science 317, 1196 (2007)
L. Li, C. Richter, J. Mannhart, and R. C. Ashoori, Nature Phys. 7, 762 (2011)
N. Pavlenko, T. Kopp, E. Y. Tsymbal, G. A. Sawatzky, J. Mannhart, arXiv:1105.1163 (2011)
M. Lee, J. R. Williams, S. Zhang, C. D. Frisbie, and D. Goldhaber-Gordon, Phys. Rev. Lett. 107, 256601 (2011)
M. Salluzzo, J. C. Cezar, N. B. Brookes, V. Bisogni, G. M. De Luca, C. Richter, S. Thiel, J. Mannhart, M. Huijben, A. Brinkman, G. Rijnders, and G. Ghiringhelli, Phys. Rev. Lett. 102, 166804 (2009)
K. Ueno, S. Nakamura, H. Shimotani, A. Ohtomo, N. Kimura, T. Nojima, H. Aoki, Y. Iwasa, and M. Kawasaki, Nature Mat. 7, 855 (2008)
Y. Lee, C. Clement, J. Hellerstedt, J. Kinney, L. Kinnischtzke, X. Leng, S. D. Snyder, and A. M. Goldman, Phys. Rev. Lett. 106, 136809 (2011)
J. Kondo, Prog. Theor. Phys. 32, 37 (1964)

About the Author

Johann Kroha is a Professor for Theoretical Physics at the Physical Institute of the University of Bonn, Germany. He received his Dr. rer. nat. degree in 1993 from the University of Karlsruhe. After extended research periods at Cornell University as an Alexander-von-Humboldt fellow, and at the University of Karlsruhe, he joined the faculty of the University of Bonn in 2002. In 2006, he was elected member of the Supervisory Council of the German Physical Society. His research interests range from strong correlations, especially Kondo physics, in quantum dot, quantum impurity, and lattice many-body systems, to the effects of disorder in electronic and photonic systems and ultracold atomic gases. In particular, he investigates, together with his group, the dynamics of these systems far from equilibrium.