Touching from a distance
Entanglement is one of the defining properties that distinguishes quantum systems from their classical counterparts. It refers to correlations between measurement outcomes on distinct (and potentially distant) degrees of freedom of a system that are stronger than those found in any classical experiment. Quantum entanglement is the key resource that enables the dramatic speedup of calculations in a quantum computer, as well as various other quantum information processing tasks.
In a paper appearing in Physical Review Letters [1], Haohua Wang and co-workers at the University of California, Santa Barbara, US, Zheijiang University, China, and NEC Corporation, Japan, have experimentally demonstrated entanglement between two spatially separated oscillating electrical circuits. This experiment represents the latest step by these researchers towards the engineering of large scale networks of controlled, entangled systems, which might be useful as quantum computers [2], or for engineering new states of quantum matter [3,4].
Harmonic oscillators would seem to be ideal building blocks for constructing highly entangled states. The harmonic oscillator is a particularly well studied exemplar: the classical physics of harmonic oscillators—such as a mass accelerated by the linear restoring force provided by a spring—is understood by high school physics students, whereas the quantum harmonic oscillator is one of the first systems to be dealt with in undergraduate quantum mechanics courses. The quantum dynamics of a harmonic oscillator can be solved exactly, and such solutions are often the starting point in the understanding of quantum field theory. Harmonic oscillators are ubiquitous in physics, and many realizations of such oscillators can be found, ranging from mechanical systems, electrical circuits, and lattice vibrations to elementary excitations of the electromagnetic field (photons).
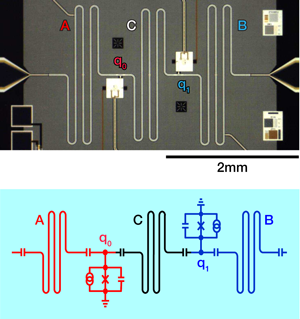
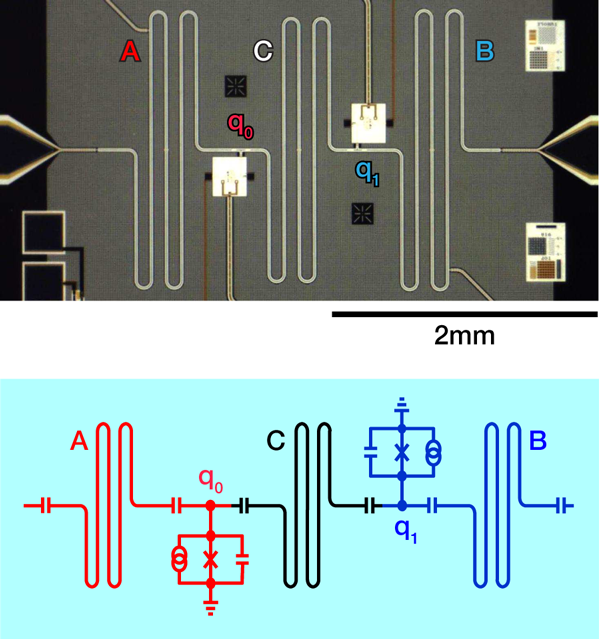
In the context of the experiment carried out by Wang et al., each harmonic oscillator consists of a coplanar waveguide resonator—equivalent to a circuit comprising a capacitor and an inductor (see Fig. 1). This resonator is superconducting at low temperature and can store excitations for a long time (in other words, it takes a relatively long time for excitations to decay—around 3μs). Excitations of this circuit can be thought of as photons—excitations of the electromagnetic field associated with the circuit elements.
Unfortunately, the simplicity of such harmonic oscillators means that a quantum system consisting solely of linearly coupled oscillators (that is, where the Hamiltonian contains coupling terms that are, at most, bilinear in the coordinate or conjugate momentum of each oscillator) is insufficient for many quantum information processing tasks. Such linear systems are not capable of implementing arbitrary quantum algorithms [5] (unless augmented with additional resources, such as single photon sources or photon-counting detectors [6]). Driving a harmonic oscillator with a classical oscillating field only allows the preparation of a restricted class of states, known as coherent states, and with only linear couplings between oscillators, it is not possible to transform such coherent initial states into entangled states of multiple oscillators. One can gain some insight into this restriction by considering the spectrum of a quantum harmonic oscillator: all the energy levels of the oscillator are equally spaced, and so it is not possible to address resonant transitions between a pair of states without also driving transitions between all other states.
Wang et al.’s experiment overcomes these limitations with the inclusion of nonlinear circuit elements: each oscillator is coupled to a superconducting phase qubit, so called because the quantum information is represented by the phase difference between the superconducting condensates on either side of an insulating barrier known as a Josephson junction (see Fig. 1) [7]. The Josephson junction is connected in parallel with a capacitor and an inductance loop. The Josephson junction adds a sinusoidal potential to the Hamiltonian of the system. The circuit is therefore no longer a purely harmonic oscillator, which means that the energy levels of the phase qubit are not equally spaced. This allows one to resonantly address a single pair of states of the phase qubit with an oscillating external field, allowing the preparation of single excitations of the qubit.
By means of a sequence of such driving pulses, together with a bias flux that shifts the qubit energy levels in and out of resonance with the central coupling resonator (denoted by C in Fig. 1), an entangled state can be established between the two phase qubits. Subsequently, this entangled state can be swapped onto the resonators A and B to create a state of the form (|01〉+|10〉)/√2. More complicated sequences of driving pulses, using higher lying states of the qubit, are used to engineer more general entangled states of the oscillators, such as the N-photon NOON state, (|N0〉+|0N〉/√2, which is a superposition of two N-photon states, where one state has all N photons in resonator A, and the other state has all photons in resonator B [8]. In the final stage of each experiment, the joint state of the two-oscillator system is established with a method called quantum tomography, again with the aid of the phase qubits. Tomography is a process by which the complete state of a quantum system can be determined via repeated preparation and measurement steps. The technique used here is a generalization of a technique pioneered by the University of California, Santa Barbara, group in a recent elegant experiment [9]. With tomographic data, Wang et al. are able to verify the entanglement of the final state, demonstrating entangled NOON states with up to three photons, although the fidelity of these entangled states is reduced somewhat by the short coherence time of the phase qubit. The entanglement in this experiment is truly macroscopic—each resonator is almost a centimeter long, and the resonators are separated by 2mm—and therefore the entangled systems are large enough to be easily resolved by the naked eye.
Numerous exciting possibilities are opened up by the techniques developed in this experiment. The ability to deterministically generate NOON states may have applications in Heisenberg limited metrology, that is, quantum assisted measurement, with accuracy beyond that implied by the standard shot noise limit [8]. The superconducting oscillators in Wang et al.’s experiment have a comparatively long coherence time ( 3μs), which is an order of magnitude larger than the coherence time for the phase qubits. Thus these oscillators may form a useful substrate for a microwave-frequency “linear optical quantum computer” [10]. Such a device may be easier to construct than a conventional, gate model quantum computer, and yet would have equivalent computational power [6].
Finally, large-scale networks of superconducting oscillators may be used to engineer new, exotic states of quantum matter. Recently, networks have been proposed that allow one to study the physics of a system of photons with broken time reversal symmetry [3], potentially allowing analogs of the quantum Hall effect for photons. Networks of entangled superconducting elements might also be useful as “protected qubits” [4,11]; that is, qubits that are inherently protected from environmental noise. These fascinating theoretical proposals might once have seemed far-fetched, but continued experimental progress along the lines reported by Wang et al. gives reason to be optimistic that they may be realized in the not-too-distant future.
References
- H. Wang, M. Mariantoni, R. C. Bialczak, M. Lenander, E. Lucero, M. Neeley, A. D. O’Connell, D. Sank, M. Weides, J. Wenner, T. Yamamoto, Y. Yin, J. Zhao, J. M. Martinis, and A. N. Cleland, Phys. Rev. Lett. 106, 060401 (2011)
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2000)[Amazon][WorldCat]
- J. Koch, A. A. Houck, K. Le Hur, and S. M. Girvin, Phys. Rev. A 82, 043811 (2010); See also the Viewpoint commentary by A. D. Greentree and A. M. Martin, Physics 3, 85 (2010)
- L. B. Ioffe and M. V. Feigel’man, Phys. Rev. B 66, 224503 (2002)
- S. L. Braunstein and P. van Loock, Rev. Mod. Phys. 77, 513 (2005)
- E. Knill, R. Laflamme, and G. J. Milburn, Nature 409, 46 (2001)
- M. H. Devoret, A. Wallraff, and J. M. Martinis, arXiv:cond-mat/0411174v1
- H. Lee, P. Kok, and J. P. Dowling, J. Mod. Opt. 49, 2325 (2002)
- M. Hofheinz et al., Nature 459, 546 (2009)
- L. Chirolli, G. Burkard, S. Kumar, and D. P. DiVincenzo, Phys. Rev. Lett. 104, 230502 (2010)
- A. Kitaev, arXiv:cond-mat/0609441v2