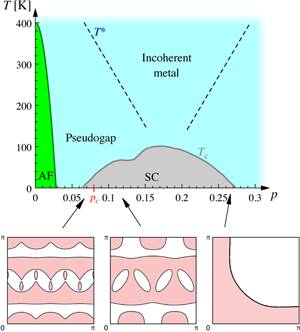
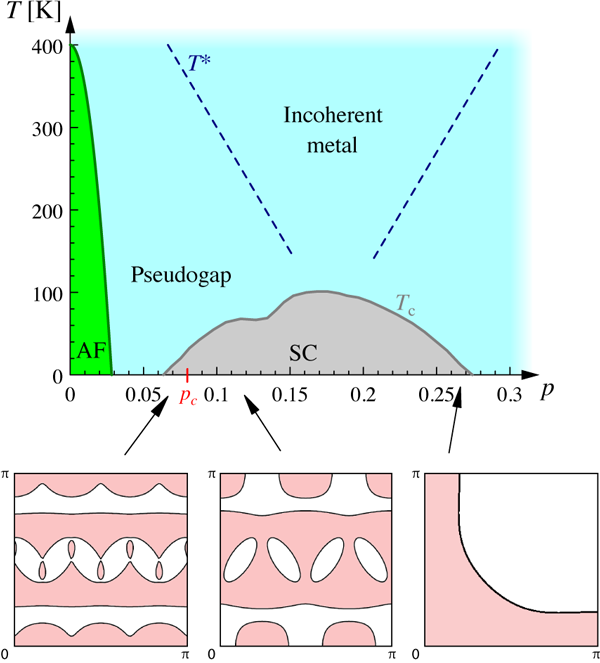
Picking the cuprates’ Fermi pockets

Matthias Vojta

Viewpoint

Picking the cuprates’ Fermi pockets

Matthias Vojta

Institut für Theoretische Physik, Technische Universität Dresden, 01062 Dresden, Germany

February 14, 2011• Physics 4, 12

Transport and quantum oscillations measurements in the cuprate superconductor

{YBa}_{2} {Cu}_{3} O_{y}

point to density-wave order as an explanation for the peculiar doping evolution of the Fermi surface.

Figure caption — **Figure 1:** (Top) Schematic phase diagram of cuprate superconductors as function of temperature $T$ and doping level $p$ . At half-filling, $p = 0$ , the materials are antiferromagnetic (AF) Mott insulators; superconductivity (SC) thus emerges from doping a Mott insulator. The doping range $p < 0.16$ ( $p > 0.16$ ) is dubbed underdoped (overdoped), and the underdoped regime, $p < 0.16$ , is characterized by the pseudogap. Quantum oscillations have been detected at low $T$ in large applied fields. (Bottom) Schematic evolution of the Fermi surface in a density-wave scenario. All panels show a quarter of the two-dimensional Brillouin zone, with occupied states shaded. On the far overdoped side, a large unreconstructed Fermi surface is seen. For smaller doping, but $p > p_{c}$ , the density-wave reconstruction induces electron pockets near $(0, π)$ , whereas those disappear for $p < p_{c}$ in favor of open orbits. (The existence of smaller pockets depends on microscopic details.)

Understanding high-temperature superconductivity in the copper oxides is considered by many as one of the most important and challenging problems in modern condensed-matter physics. It is, however, not just the superconducting state that presents unresolved questions, but also the nonsuperconducting normal state of these materials is anything but ordinary. At small carrier doping into the parent insulating compounds, the dominant feature is the so-called pseudogap regime [1], where low-energy states disappear upon cooling below a characteristic temperature $T^{*}$ (see Fig. 1). The origin of this phenomenon is hotly debated and believed to be the key to the solution of the problem of why cuprate compounds have such a high- $T_{c}$ .

Over the past few years, sophisticated quantum oscillation measurements have been used to map the Fermi surface of the cuprate’s charge carriers [2,3]. One of the puzzling results is that the quantum oscillation signal disappears if the carrier concentration through doping is lower than a certain critical value [4], indicating a yet unexplained quantum phase transition. Presenting the results of an important set of new experiments in Physical Review B [5], David LeBoeuf at the Université de Sherbrooke, Canada, and collaborators in the US, Canada, and France, have made a significant discovery concerning this peculiar transition. The data demonstrate a striking correlation between two experimental approaches—quantum oscillation and transport measurements—which gives information on what happens to the Fermi surface as the doping is changed. The results are found to be consistent with a one-dimensional density-wave modulation, the so-called “stripes”—which have also been observed in other cuprate superconductors—being the cause of the abrupt change in the Fermi surface [6,7]. This implies that stripes [8,9] are much more common to cuprates than previously thought and that they form an integral part of the pseudogap phenomenology.

To appreciate these experimental findings, it is instructive to recall important cuprate characteristics. The key action in cuprate superconductors is believed to occur in the ${CuO}_{2}$ layers to which the transition metal ions ( $Y$ , $Ba$ , $La$ , $Sr$ , etc.) contribute carriers. The so-called parent compounds, like ${La}_{2} {SrCu}_{4}$ and ${YBa}_{2} {Cu}_{3} O_{6}$ , are half-filled Mott insulators, where the strong mutual repulsion among electrons prevents their motion, making them insulators even though band theory predicts they should conduct. The unpaired $Cu$ $3 d$ electrons form magnetic moments, which order antiferromagnetically.

Chemical doping changes the carrier concentration $p$ (Fig. 1), which first leads to the suppression of antiferromagnetism and then to the appearance of superconductivity. While the properties deep inside the superconducting state appear to be qualitatively well captured by BCS theory, which describes conventional superconductors like lead and niobium, the normal-state properties are highly anomalous, particularly the underdoped pseudogap region below $T^{*}$ and also the region above $T_{c}$ around optimal doping ( $p \approx 0.16$ ) (see Fig. 1). In the latter “incoherent metal,” the resistivity obeys $ρ \propto T$ over a wide range of temperatures, in striking contrast to a Fermi-liquid $T^{2}$ law, expected for conventional metals. Thus cuprate superconductivity does not emerge from conventional metallic behavior, but rather from the doping of a Mott insulator [10].

Experimental data characterizing the pseudogap regime have seen a spectacular evolution over the last years [1,11]. It was long believed that coherent electronic quasiparticles do not exist in this regime, an absence that was hypothesized mainly because early photoemission experiments only detected broad features in the single-electron spectrum. The most important breakthrough in this debate was the detection of definitive quantum oscillations in high magnetic fields in 2007 by Taillefer’s group in ${YBa}_{2} {Cu}_{3} O_{6.5}$ with $p = 0.10$ [2], subsequently verified and also extended to ${YBa}_{2} {Cu}_{4} O_{8}$ [3]. Why are quantum oscillation experiments so informative? Quantum oscillations arise from the motion of electrons on closed fixed-energy orbits in momentum space perpendicular to the applied field $B$ . The orbits’ quantization results in oscillations in $1 / B$ of observables such as the magnetic susceptibility, with the period being inversely proportional to the momentum-space area of the orbit. In a two-dimensional metal, the oscillations allow one to directly extract the Fermi-surface area. Applying this analysis to the cuprates, the quantum-oscillation experiments indicate the existence of tiny Fermi pockets, which are incompatible both with the “large” Fermi surface of $(1 - x)$ electrons expected in a conventional metal, and with a possible “small” Fermi surface of $x$ holes proposed for doped Mott insulators [10]. Thus coherent quasiparticles appear to be present, but with an unexpected type of Fermi surface. An additional notable feature is the negative low-temperature Hall coefficient $R_{H}$ in the regime where quantum oscillations are observed, suggesting that the Fermi surface of the dominant carriers is electronlike instead of holelike [12].

One possible explanation for most of these features is a Fermi-surface reconstruction due to density-wave order. Bragg scattering from the density wave will open gaps in the electron’s band structure, such that the original Fermi surface breaks up into small pockets of both electron and hole character. We already know that cuprates of the ${La}_{2 - x} {Sr}_{x} {CuO}_{4}$ family display stripelike density-wave order [8,9], and indications of field-induced spin-density-wave order have also been reported for ${YBa}_{2} {Cu}_{3} O_{y}$ [13].

A recent detailed study [4] of quantum oscillations in ${YBa}_{2} {Cu}_{3} O_{y}$ of different doping levels revealed that quantum oscillations disappear for doping levels $p$ smaller than a critical $p_{c} \approx 0.08$ , with clear signatures of a continuous quantum phase transition at $p_{c}$ (Fig. 1 ). This was interpreted in terms of an underlying metal-to-insulator transition.

In this context, the findings of LeBoeuf et al. [5] are very interesting. The authors study both resistivity and Hall effect of ${YBa}_{2} {Cu}_{3} O_{y}$ at high magnetic fields over a large range of temperatures and doping concentrations ( $0.078 \leq p \leq 0.152$ ). The most significant discovery is that the low-temperature high-field Hall coefficient changes sign at the same concentration, $p_{c}$ , at which the quantum oscillations disappear, i.e., $R_{H} > 0$ for $p < p_{c}$ and $R_{H} < 0$ for $p > p_{c}$ . In contrast, the Hall coefficient at $100 K$ is positive for all $p$ , i.e., the dominant negative Hall signal for $p > p_{c}$ only emerges at low $T$ , with doping-dependent downturn ( $T_{H}$ ) and zero-crossing ( $T_{0}$ ) temperatures of $R_{H}$ . Furthermore, resistivity measurements show that the small- $p$ positive Hall signal correlates with a low-temperature upturn in $ρ (T)$ , which is present for $p < p_{c}$ but not for $p > p_{c}$ , previously associated with a metal-to-insulator crossover.

The collected data of Refs. [4] and [5] strongly support the scenario of a doping-dependent Fermi-surface reconstruction in ${YBa}_{2} {Cu}_{3} O_{y}$ at low temperatures and high fields, such that electron pockets are present for $p > p_{c}$ , which dominate most transport properties. The most plausible origin of the Fermi-surface reconstruction is indeed density-wave order. Various theoretical calculations have shown that spin-density-wave order produces an electron pocket near $(0, π)$ over some range of parameters. By analogy with ${La}_{2 - x} {Sr}_{x} {CuO}_{4}$ cuprates, one expects that the modulation period of the density wave increases with decreasing $p$ , such that some Fermi pockets merge and disappear below a critical $p_{c}$ , giving way to a Fermi surface with one-dimensional open orbits [7]. A possible Fermi-surface evolution is shown in the bottom panels of Fig. 1.

This means that the quantum phase transition at $p_{c}$ is not a metal-to-insulator transition, as had been previously assumed, but instead a Lifshitz transition inside a density-wave phase where the electron pockets disappear [7]. Assuming that the electron pockets have a significantly higher mobility than the remaining orbits qualitatively explains most of the transport data. The presence of one-dimensional orbits for $p < p_{c}$ is, furthermore, consistent with the evolution of the in-plane resistivity anisotropy [5]. Finally, the authors of Ref. [5] point to a similarity between the ${YBa}_{2} {Cu}_{3} O_{y}$ transport data and that obtained on stripe-ordered cuprates of the ${La}_{2 - x} {Sr}_{x} {CuO}_{4}$ family, where a significant low- $T$ drop of $R_{H}$ has been observed as well.

Taken together, the experimental observations can be considered as strong evidence for density-wave order in ${YBa}_{2} {Cu}_{3} O_{y}$ at low temperatures and high fields. Of course, the following important questions remain.

(i) What is the role of the magnetic field in the experiments of LeBoeuf et al. [5]? Does it merely enable transport measurements by suppressing superconductivity, or does it actually induce the density-wave order? The answer is not obvious: On the one hand, various characteristic transport signatures, such as sign change in $R_{H} (T)$ at $p > p_{c}$ and the apparent metal-to-insulator crossover, are present at zero field as well. On the other hand, it is known from neutron scattering that an applied field strongly enhances spin-density-wave order in ${YBa}_{2} {Cu}_{3} O_{y}$ [13].

(ii) Is the $R_{H}$ -downturn temperature $T_{H}$ indeed to be interpreted as the onset of strong fluctuations of the density-wave order, as suggested by LeBoeuf et al. [5]? Notably, $T_{H}$ monotonously decreases with doping, whereas experiments in other cuprates indicate that both strength and onset temperature of stripe order are largest at $p = 1 / 8$ doping and decrease from there upon reducing $p$ [14,15]. This issue is crucial in order to clarify the relation between the enigmatic pseudogap and the emergence of density-wave order.

While the question of whether stripes are crucial to understand the pairing mechanism responsible for superconductivity in cuprates is still open, these findings set a significant new constraint on an eventual theory.

References

T. Timusk and B. W. Statt, Rep. Prog. Phys. 62, 61 (1999)
N. Doiron-Leyraud et al., Nature 447, 565 (2007)
E. A. Yelland et al., Phys. Rev. Lett. 100, 047003 (2008)
S. E. Sebastian et al., Proc. Natl. Acad. Sci. U.S.A. 107, 6175 (2010)
D. LeBoeuf et al., Phys. Rev. B 83, 054506 (2011)
A. J. Millis and M. R. Norman, Phys. Rev. B 76, 220503 (2007)
M. R. Norman, J. Lin, and A. J. Millis, Phys. Rev. B 81, 180513 (2010)
S. A. Kivelson et al., Rev. Mod. Phys. 75, 1201 (2003)
M. Vojta, Adv. Phys. 58, 699 (2009)
P. A. Lee, N. Nagaosa, and X.-G. Wen, Rev. Mod. Phys. 78, 17 (2006)
M. R. Norman, Physics 3, 86 (2010)
D. LeBoeuf et al., Nature 450, 533 (2007)
D. Haug et al., Phys. Rev. Lett. 103, 017001 (2009)
C. V. Parker et al., Nature 468, 677 (2010)
J. Fink et al., arXiv:1011.5101

About the Author

Matthias Vojta received his Ph.D. from Dresden Technical University, Germany, in 1998. After postdoctoral positions at Yale and Augsburg and faculty appointments at Karlsruhe and Cologne, he is now Professor of Physics at Dresden. His research interests are in theoretical condensed-matter physics and include quantum phase transitions, high-temperature superconductors, heavy fermions, frustrated magnets, as well as quantum impurities and quantum dots. Currently, he is acting as a Divisional Associate Editor of Physical Review Letters.

Lifshitz critical point in the cuprate superconductor ${YBa}_{2} {Cu}_{3} O_{y}$ from high-field Hall effect measurements

David LeBoeuf, Nicolas Doiron-Leyraud, B. Vignolle, Mike Sutherland, B. J. Ramshaw, J. Levallois, R. Daou, Francis Laliberté, Olivier Cyr-Choinière, Johan Chang, Y. J. Jo, L. Balicas, Ruixing Liang, D. A. Bonn, W. N. Hardy, Cyril Proust, and Louis Taillefer

Phys. Rev. B 83, 054506 (2011)

Published February 14, 2011

Read PDF