Signal amplification through bifurcation in nanoresonators

Mark I. Dykman

Viewpoint

Signal amplification through bifurcation in nanoresonators

Mark I. Dykman

Department of Physics and Astronomy, Michigan State University, East Lansing, MI 48824, USA

February 28, 2011• Physics 4, 16

A pair of coupled nanomechanical resonators are used in a novel way to amplify a weak signal.

Figure caption — **Figure 1:** (Top) A sketch of the system, which is a pair of $6 \times 0.5 \times 0.2$ $μ$ $m$ doubly clamped nanobeams with $400 nm$ separation. The beams were illuminated by an infrared laser focused to a spot of $10$ $μ$ $m$ and the reflected signal was detected. (Bottom) The effective potential for the slow coordinate $q_{2}$ of the higher-frequency nanobeam for different values of the modulation frequency $ω_{p}$ ; | $q_{2}$ | gives the scaled amplitude of the vibrations at frequency $ω_{p} / 2$ , whereas the sign of $q_{2}$ determines their phase.

The small size of micro- and nanomechanical resonators, combined with the slow decay of their vibrational modes, enable numerous applications of these devices—from the studies of macroscopic quantum phenomena [1,2], to mass detection with single-atom sensitivity [3,4], to imaging with single-atom and single-spin resolution [5]. An important feature of nanoresonators is the vibration nonlinearity, which becomes significant even at small vibration amplitudes. It allows investigating a broad variety of nonlinear phenomena, including basic phenomena such as bifurcations, where the number of stable states of the system, or the character of motion, change with varying parameters. A typical example is the onset of parametric resonance, where a resonator starts vibrating at half the frequency at which it is modulated. Nonlinear dynamics near bifurcation points is particularly interesting as it is controlled by one, or a few, slow variables [6] and displays universal system-independent features, such as scaling behavior.

In a paper published in Physical Review Letters, Rassul Karabalin and colleagues [7] from Caltech, US, and Tel Aviv University, Israel, propose and implement a new bifurcation-based amplification scheme using coupled nanoresonators and demonstrate that it can be employed for robust small-signal amplification. The results bear not only on the fast expanding field of bifurcation-based amplification [8], but also on the physics of classical and quantum fluctuation phenomena in nonlinear vibrational systems, and on the dynamics and fluctuations near bifurcation points.

Conventional bifurcation amplifiers utilize bifurcations where, as the input changes, the state occupied by the system disappears and the system switches to a different state. For example, in Josephson bifurcation amplifiers used in quantum measurements, the system switches between vibrational states with different amplitudes and phases [8]. This is similar to magnetization switching in single-domain magnets once an external magnetic field exceeds a critical value. The bifurcation amplifier by Karabalin et al. works in a different way. Here, as the control parameter is varied, the system goes to the state with either large or small output, depending on the input signal; that is why the authors call the device a bifurcation-topology amplifier.

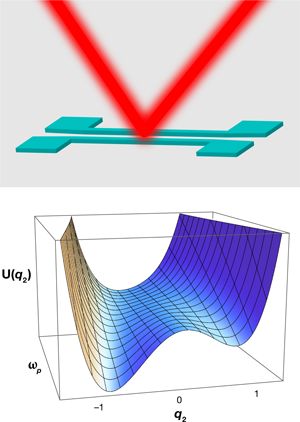
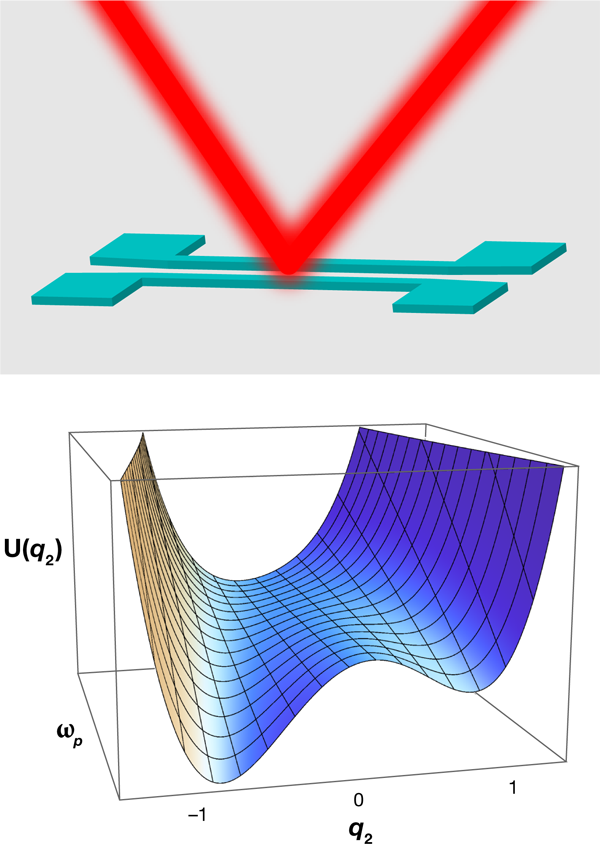
Their system is sketched in the top panel of Fig. 1. It consists of two nearly identical nanoresonators, $1$ and $2$ . The eigenfrequencies $ω_{1}$ and $ω_{2}$ of their fundamental flexural (bending) modes are close in value by design. The modes are underdamped, allowing a strong response in resonant conditions. The stiffness of the resonators, and thus the values of $ω_{1}$ and $ω_{2}$ , is modulated at a frequency $ω_{p}$ close to $2 ω_{1, 2}$ . For a single resonator, such modulation can lead to parametric resonance with the onset of two vibrational states that have equal amplitudes and frequency $ω_{p} / 2$ but differ in phase by $π$ . In the experiment, the vibrations are detected by optical interferometry using a laser beam reflected from the resonators.

The key feature of the amplifier is that the distance between the resonators is small compared to the laser beam diameter. Therefore, the optical response is large if the resonators are vibrating in phase, as in this case the reflected signals coherently interfere; if the vibrations are in counterphase, the reflection is suppressed. The idea put forward by Karabalin et al. is that the relative phase of the resonators can be controlled by a weak input signal, which will then trigger a large response with amplitude determined by the amplitude of the parametrically excited vibrations.

The resonators are parametrically excited by ramping up the modulation frequency $ω_{p}$ across the bifurcational values $ω_{B 1, 2}$ . Let us assume that resonator 1 is slightly “softer” than resonator $2$ , i.e., $ω_{1} < ω_{2}$ and $ω_{B 1} < ω_{B 2}$ . Then, if we start from low $ω_{p}$ , resonator $1$ will be excited first, once $ω_{p}$ reaches $ω_{B 1}$ . If the resonators are uncoupled, resonator $2$ will be excited later, at $ω_{p} = ω_{B 2}$ . Its phase can be close or opposite to the phase of resonator $1$ , with equal probability. Because the vibration amplitudes increase near bifurcation points as $(ω_{p} - ω_{B 1, 2})^{1 / 2}$ , depending on this phase, the output signal of the two resonators will either quickly increase or decrease with the increasing $ω_{p}$ .

The situation is different if the resonators are interacting. Since the vibration amplitudes are small compared to the inter-resonator spacing, the force on one resonator from the other is approximately linear in their relative displacement. Once resonator $1$ is excited with increasing $ω_{p}$ , it exerts a periodic force on resonator $2$ at frequency $ω_{p} / 2$ . This force lifts the degeneracy of the vibrations of resonator $2$ with opposite phases [9,10].

Both the force and the displacement of resonator $2$ in a stable vibrational state become approximately time-independent if one switches to a reference frame rotating at frequency $ω_{p} / 2$ . Resonator $2$ then is reminiscent of a system that undergoes a symmetry-breaking transition in the presence of a static field. As such, it can be described by the Landau mean-field theory with an order parameter $q_{2}$ that moves in a potential $U (q_{2})$ , shown in the bottom panel of Fig. 1. The minima of the potential correspond to stable vibrational states with amplitudes $\propto | q_{2} |$ and phases that depend on the sign of $q_{2}$ ; for the values of $q_{2}$ with opposite signs and the same | $q_{2} |$ , the phases differ by $π$ .

With no interaction, the potential $U (q_{2})$ is a symmetric quartic parabola. Its shape varies with $ω_{p}$ from a single well for $ω_{p} < ω_{B 2}$ , with the minimum at $q_{2} = 0$ , to a double well for $ω_{p} > ω_{B 2}$ . The wells are located at equal and opposite in sign $q_{2}$ , and they are equally likely to be occupied once $ω_{p}$ crosses $ω_{B 2}$ . The weak biasing force from the interaction breaks the symmetry. It shifts the minimum of $U (q_{2})$ slightly away from $q_{2} = 0$ for $ω_{p}$ below $ω_{B 2}$ . But now, with increasing $ω_{p}$ , the system follows the trough of $U (q_{2})$ , as shown in the bottom panel of Fig. 1, and the choice of the well is no longer random.

As seen in Fig. 1, | $q_{2}$ | at the potential minimum sharply increases with $ω_{p}$ for $ω_{p} > ω_{B 2}$ . This leads to the amplification by the bifurcation amplifier, with the input signal being the biasing force and ultimately the coupling between the nanoresonators. It is clear from qualitative arguments, and also follows from the analysis that, if the interaction between the resonators is attractive, the resulting phase of resonator $2$ is close to the phase of resonator $1$ , whereas for repulsive interaction the resonators are in counterphase.

In the experiment, the amplified signal is determined by the voltage between the top and bottom surfaces of the nanobeams, which are $GaAs$ layered structures. The voltage leads to the same-sign polarization of the nanobeams, and thus to their repulsion (characteristic of parallel electrostatic dipoles). The dc component of the voltage is adjusted so as to compensate for the residual attraction from the elastic coupling through the shared support. The signal itself is the additional voltage $V_{in} (t)$ . The net coupling between the nanobeams is proportional to $V_{in} (t)$ and can correspond to either attraction or repulsion.

To understand the observed response, it is necessary to take into consideration the noise in the system. The sensitivity to noise is particularly high where $ω_{p}$ goes through the vicinity of $ω_{B 2}$ , as here it is comparatively easy to sway the system between the troughs of $U (q_{2})$ , causing loss of information about the bias. However, even where the signal is weak compared to the noise, it still leads to the preferred occupation of the deeper trough. The situation is somewhat reminiscent of stochastic resonance in a bistable system, where, in the presence of noise, even a weak input signal modulates the state occupations. In both cases, the effect of a weak signal is described by linear response theory, but for the present bifurcation topology amplifier it depends on the ratio of the signal to the square root of the noise intensity, rather than to the noise intensity in stochastic resonance [11]; it also depends on the rate at which $ω_{p}$ is swept. The developed theory is not limited to linear response and provides a quantitative prediction of the dependence on the resonator coupling of the probabilities of occupying the states with close and opposite phases. Both linear response and the interesting characteristic nonlinear effects are clearly seen in the experiment.

Already in this first experiment, a signal $V_{in} = 1 mV$ is resolved that corresponds to $\sim 70$ electrons on the resonators’ electrodes. The analysis of the noise sources indicates that a significant enhancement of the charge sensitivity, potentially up to $\sim 10^{- 5} e / \sqrt{Hz}$ , should be attainable by going from the present device, with frequencies $ω_{1, 2} / 2 π \sim 13 MHz$ , to an optimized $GHz$ device operating at cryogenic temperatures. This opens a new area of applications of nanoelectromechanical systems. Moreover, the proposed highly sensitive bifurcation amplifier can also be implemented with other systems, for example, with nonlinear microwave cavities where parametric excitation was recently demonstrated in the quantum regime [12]. Besides applications, this may lead to a better understanding of quantum and classical fluctuations in systems far from thermal equilibrium.

References

H. B. Chan, V. A. Aksyuk, R. N. Kleiman, D. J. Bishop, and F. Capasso, Science 291, 1941 (2001)
A. D. O’Connell et al., Nature 464, 697 (2010)
K. Jensen, K. Kim, and A. Zettl, Nature Nanotech. 3, 533 (2008)
H.-Y. Chiu, P. Hung, H. W. C. Postma, and M. Bockrath, Nano Lett. 8, 4342 (2008)
D. Rugar, R. Budakian, H. J. Mamin, and B. W. Chui, Nature 430, 329 (2004)
J. Guckenheimer and P. Holmes, Nonlinear Oscillators, Dynamical Systems and Bifurcations of Vector Fields, Applied Mathematical Sciences, Vol. 42 (Springer-Verlag, New York, 1997)[Amazon][WorldCat]
R. B. Karabalin, R. Lifshitz, M. C. Cross, M. H. Matheny, S. C. Masmanidis, and M. L. Roukes, Phys. Rev. Lett. 106, 094102 (2011)
R. Vijay, M. H. Devoret, and I. Siddiqi, Rev. Sci. Instrum. 80, 111101 (2009)
P. Bryant and K. Wiesenfeld, Phys. Rev. A 33, 2525 (1986)
D. Ryvkine and M. I. Dykman, Phys. Rev. E 74, 061118 (2006)
M. I. Dykman, D. G. Luchinsky, R. Mannella, P. V. E. McClintock, N. D. Stein, and N. G. Stocks, Nuovo Cimento D 17, 661 (1995)
C. M. Wilson, T. Duty, M. Sandberg, F. Persson, V. Shumeiko, and P. Delsing, Phys. Rev. Lett. 105, 233907 (2010)

About the Author

Mark Dykman is a professor of physics at Michigan State University. He has worked on various topics, including effects resulting from the interplay of decoherence, nonlinearity, and fluctuations in mesoscopic vibrational systems; Floquet dynamics of dissipative systems; transport in correlated electron systems; nonlinear optics of solids; rare events in far-from-thermal-equilibrium systems; and many-body aspects of quantum information. He is a Fellow of the American Physical Society. In 2013 he was recognized as an Outstanding Referee by the American Physical Society.