A defect controls transport in graphene
The field of spintronics, which uses the spin of an electron besides its charge as a carrier of information in electronics, has seen much theoretical and experimental progress over the last decades [1]. The spin degree of freedom interacts less with its environment than does the charge degree of freedom. Hence spin-based electronics may have some advantages—less dissipation of power, for example—over charge-based ones. Since spin is the intrinsic angular momentum of an electron, found in each and every electronic system, the efficacy of a specific material for spintronics depends on how well it can control and store spin.
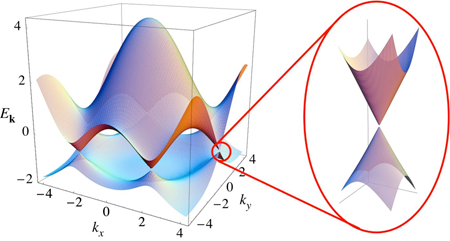
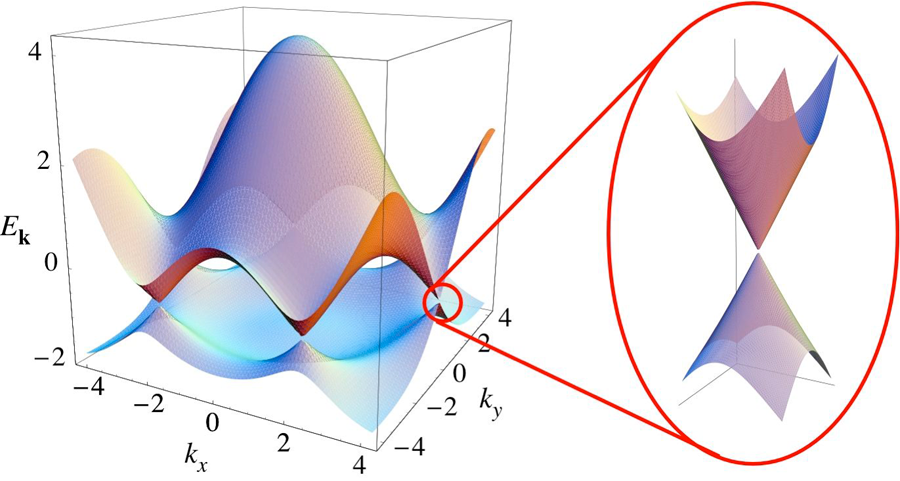
Can we find additional degrees of freedom—similar to the electron spin—as alternative carriers of information? The answer is yes. For instance, graphene, in which carbon atoms are arranged in a two-dimensional honeycomb lattice, has two pseudospin degrees of freedom in addition to the electron spin. These pseudospin degrees of freedom behave in a mathematically similar way to the electron spin, i.e., they act like additional intrinsic angular momenta of the electron. The pseudospins are both related to the peculiar band structure of graphene, shown in Fig. 1. One is called sublattice pseudospin and the other valley isospin. The former occurs due to the bipartite honeycomb lattice, which has two distinct sublattices. Whenever the direction of motion of the electron changes, the sublattice pseudospin also has to change and realign to the new direction of motion [2]. Therefore it is vulnerable to disorder and apparently not useful as a carrier of information. In this it differs from the valley isospin, which distinguishes between the two independent valleys in the band structure of graphene, commonly called K and K′, see Fig. 1. The valley isospin is more robust against disorder than the sublattice pseudospin as it needs a large momentum transfer (on the order of the inverse lattice spacing of graphene) to scatter from K to K′. This offers the possibility of developing valleytronics devices that are similar in concept to spintronics devices.
A seminal paper [3] in 2007 came with a proposal for using the valley degree of freedom as a carrier of information. Its authors analyzed a valley filter and a valley valve based on a graphene nanoribbon with zigzag edges. In a valley filter, the idea is that a particle with a given valley degree of freedom, say K, is transmitted, and a particle with the opposite valley degree of freedom is reflected. The device proposal in Ref. [3] is based on a graphene nanoribbon cut along a high symmetry axis of the honeycomb lattice (called a zigzag edge). For this device to work, it is ideal to have a graphene nanoribbon with zigzag edges because the lowest transverse mode of such a nanoribbon is known to be valley-polarized [4]. This is a special property of the zigzag edge. Interestingly, it can be used to introduce a valley polarization in graphene, meaning that an outgoing stream of particles would contain electrons having preferably one of the two isospin degrees of freedom. Even though this work stimulated a considerable amount of interest in finding ways to manipulate the valley isospin (a nice example is the valley Hall effect [5]), none have been experimentally realized. At the moment, narrow graphene nanoribbons with perfect zigzag edges do not exist, although unzipping nanotubes may be a possibility [6].
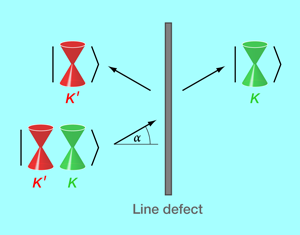
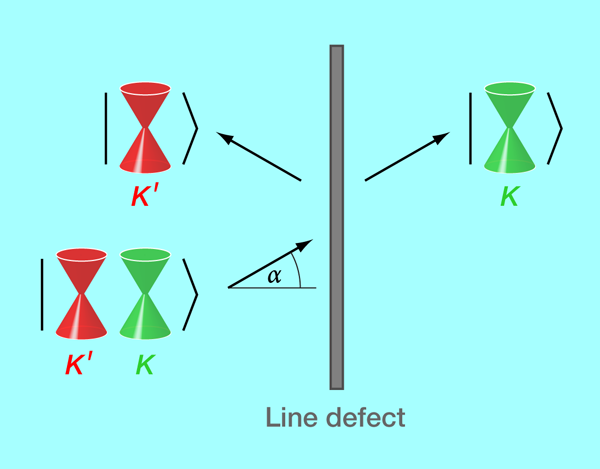
In a paper in Physical Review Letters [7], Daniel Gunlycke and Carter T. White from the US Naval Research Laboratory propose a valley filter in single-layer graphene that does not rely on either quantum confinement or any specific type of edges. The valley filtering is created—see Fig. 2 for a schematic of the proposed setup—at an extended line defect that is a periodic sequence of octagonal and pentagonal sp2-hybridized carbon rings. This defect was recently observed [8] in graphene on a nickel substrate.
The whole structure (graphene with a one-dimensional topological defect) is mirror-symmetric with respect to the axis defined by the line defect. This reflection symmetry is key to why the line defect works as a valley filter. Let us first describe the working principle of the valley filter and get back to the symmetry argument below. Gunlycke and White analyzed the transmission probability across the line defect for an incoming electron as a function of the angle of incidence. They showed that the valley polarization P=PK-PK′, where Pm(m=K,K′) is the probability that a transmitted electron has valley index m, can be approximated by sinα. Here, α is the angle of incidence with respect to the normal of the line defect, see Fig. 2. Hence the line defect acts like a perfect valley filter for α close to π/2. The authors claim that this effect is robust against certain perturbations like interactions across the line defect and potentials on the line defect and their neighboring sites. Therefore angle-dependent transmission measurements across such a line defect might in fact be an option for an experimental realization of a valley filter.
How can we understand the performance of this valley filter device, based on symmetry arguments? Gunlycke and White argue that in the limit of vanishing quasiparticle energy ε→0 (i.e., directly at the Dirac point in graphene, see Fig. 1), the reflection operator about the line defect commutes with the following three Hamiltonians: (i) Hm(m=K,K′) representing graphene (for a given valley m), (ii) the Hamiltonian of the isolated line defect, and (iii) the Hamiltonian representing the interaction between graphene and the line defect. Consequently, the eigenstates of Hm are either symmetric (|+〉) or antisymmetric (|-〉) with respect to reflection. The incoming state approaching the line defect is, for generic α, a superposition of |+〉 and |-〉. Since only symmetric states can carry electrons across the line defect, one can estimate the transmission probability of a quasiparticle with valley index m by projecting the incoming state on the symmetric (|+〉) component. This analysis yields P=sinα, as stated above. Although the symmetry arguments are strictly valid only at ε→0, the authors show by a more elaborate numerical transport calculation that the result remains true for finite quasiparticle energies ε, as long as ε≪hvF/(2πa) (which corresponds to the large energy of 2.3eV; a is the lattice constant and νF the Fermi velocity of graphene).
Can valleytronics ever compete against spintronics? We remain a bit skeptical. Although scattering from K to K′ calls for a large momentum transfer, it may still happen in realistic graphene devices. The reason is that the edges of the graphene flake or adatoms that stick to the surface can provide sharp enough scattering potentials to mix K and K′. Once K and K′ are mixed, the performance of the valley filter will be altered. A big advantage of the proposal by Gunlycke and White based on the line defect observed in Ref. [8] is that it should suffer much less from this type of disorder compared to previous proposals based, for instance, on edged graphene nanoribbons.
References
- S. A. Wolf et al., Science 294, 1488 (2001); I. Zutic, J. Fabian, and S. Das Sarma, Rev. Mod. Phys. 76, 323 (2004)
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, Rev. Mod. Phys. 81, 109 (2009)
- A. Rycerz, J. Tworzydlo, and C. W. J. Beenakker, Nature Phys. 3, 172 (2007)
- M. Fujita, K. Wakabayashi, K. Nakada, and K. Kusakabe, J. Phys. Soc. Jpn. 65, 1920 (1996)
- D. Xiao, W. Yao, and Q. Niu, Phys. Rev. Lett. 99, 236809 (2007)
- D. V. Kosynkin et al., Nature 458, 872 (2009); L. Jiao et al., 458, 877 (2009)
- D. Gunlycke and C. T. White, Phys. Rev. Lett. 106, 136806 (2011)
- J. Lahiri, Y. Lin, P. Bozkurt, I. I. Oleynik, and M. Batzill, Nature Nano. 5, 326 (2010)