Iron Superconductivity Weathers Another Storm

Iron-based high-temperature superconductors were discovered in January 2008, and they have arguably been the biggest news in the field of superconductivity since the appearance of the cuprate superconductors in the late eighties [1]. Although the cuprates demonstrated that high-temperature superconductivity was possible, the iron-based materials prove that this phenomenon is not limited to a single class of compounds.

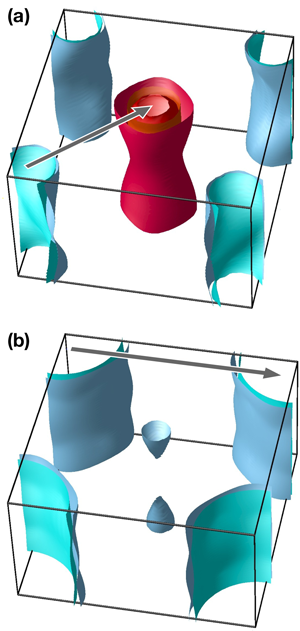
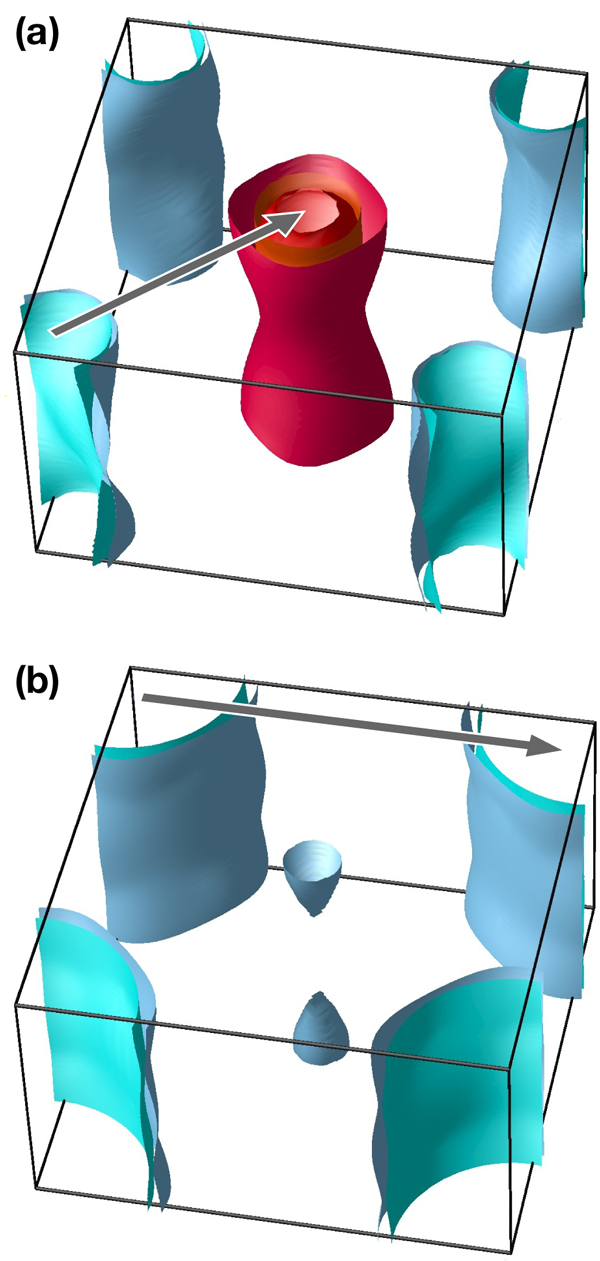
So far, the story unraveling about the new iron-based superconductors has been quite rewarding for practitioners. In order to appreciate the relevant timescales, remember that for the cuprates, nearly ten years passed before a general consensus was reached on the pairing symmetry, and consider that there still is no agreement on the underlying mechanism. More in line with the story of superconductivity in ${\text{MgB}}_2$, where full consensus was achieved within a year, a plausible model was proposed within weeks after the discovery of iron-based superconductors [2] and gained support from the majority of researchers in the field. In this model, the calculated and experimentally confirmed [1] electronic band structure of iron-based superconductors is semimetallic, consisting of hole and electron Fermi surface pockets, separated by a ( $\pi$, $\pi$) wave vector in momentum space (see Fig. 1). This suggests the existence of a spin excitation with the same wave vector, which was indeed found experimentally [3]. If one considers this spin excitation to be the pairing agent for superconductivity [1], the resulting order parameters for the holes and for the electrons will have opposite signs, with the overall angular momentum being $L=0$ ( $s$-type); hence the name $s_{\pm }$.

Credit: Alan Stonebraker

Credit: Alan Stonebraker

×

This simple concept has been questioned on at least two occasions when new iron-based superconducting materials were discovered. This happened first when two low- $T_c$ compounds, ${\text{KFe}}_2{\text{As}}_2$ and $\text{LaFePO}$, exhibited clear signs of gap nodes [4], which are not required by symmetry in the $s_{\pm }$ model. Theoretically, this could still be rationalized within an $s_{\pm }$ spin-fluctuation-induced superconductivity model. Indeed, if there are other competing interactions, e.g., with phonons, or a particularly strong Coulomb repulsion, a compromise can be found that results in gap nodes. However, this point of view is substantially based on the fact that both ${\text{KFe}}_2{\text{As}}_2$ and $\text{LaFePO}$ have rather low critical temperatures. So, when a third compound was found clearly exhibiting nodes, this explanation was severely shaken; the compound in question was phosphorus-doped ${\text{BaFe}}_2{\text{As}}_2$, with $T_c$ in excess of $30\text{K}$ [4].

Numerous model calculations appeared then, in which the combination of the angular dependence of the orbital character of electronic bands and a strong Coulomb repulsion led to patches of the “wrong” sign of the order parameter, and thus to nodes [5]. Of course, whether this regime is realized or not depends on the material in question; it is quite normal that some compounds are in the “nodal” region in the parameter space, while others are not. This explanation, though it seems natural, is not without problems: Retardation effects (different energy scales for the superconducting pairing and the static electronic interactions) cause a renormalization of the Coulomb repulsion; it becomes much less important than that appearing in the static calculation, if not negligible. Most importantly, such calculations yield strongly anisotropic gaps in all compounds, whether nodal or not. However, angle-resolved photoemission spectroscopy (ARPES) shows uniform gaps wherever it can map the electronic Fermi surface. Yet there was a feeling in the community that even though our favorite model may have some quantitative issues, it was conceptually correct, and had all the necessary potential to overcome its problems; the quantitative details would eventually be ironed out.

Once again, doubt was cast on this model when another compound was found, ${\text{Sr}}_2{\text{VO}}_3\text{FeAs}$ [6], which according to band structure calculations featured vanadium electrons at the Fermi surface in addition to electrons and holes from iron, completely destroying the neat dichotomy of the Fermi surfaces into well-separated electron and hole pockets. However, it was soon discovered that the vanadium electrons, unlike the iron ones, are strongly correlated in this system, and thus are completely removed from the Fermi level [7]. This, of course, saves the model.

Thus, barring a few dissenters, towards the end of 2010 there was a general consensus that even if the $s_{\pm }$ model may have problems with some measurements, compared to alternatives it accounts for the entire body of the experiments in a much better way.

In November of 2010, another torpedo exploded under the $s_{\pm }$ ship. A new superconductor was reported, believed to be ${\text{K}}_{0.8}{\text{Fe}}_2{\text{Se}}_2$ [8]. A formal electron count makes this compound electron-doped at the level of $0.4e$ per $\text{Fe}$. That doping is nominally the same as for $\text{Ba}({\text{Fe}}_{0.6}{\text{Co}}_{0.4}{)}_2{\text{As}}_2$, but the latter is located way past the superconducting dome of the $\text{Co}$-doped system, and way past the level of doping at which the hole pockets sink completely under the Fermi level.

Band structure calculations, in full agreement with common sense, produce large electron Fermi surfaces at the ( $\pm \pi$, $\pm \pi$) points in the Brillouin zone (see Fig. 1). The first reaction of theorists, including the author of this article, was that the quasinesting between the hole and electron pockets in pnictides is supplanted by the quasinesting between the electron pockets, which naturally results in some sort of a $d$-wave state (see Refs. [9,10]). This is most likely wrong. Indeed, one can show from very general symmetry considerations that such a state must necessarily have nodes [10], and it was shown rather quickly by means of ARPES that there are no nodes in this superconductor [11]; that was also confirmed by NMR [12] and specific heat studies [13].

On the other hand, the prerequisites from the $s_{\pm }$ model are clearly missing in this material. One can think about a plain, more-or-less uniform $s$-wave state, but just the proximity to magnetism speaks against this option, as spin fluctuations are destructive for that kind of superconducting state. Another possibility, compatible with the ARPES-reported Fermi surfaces, is a different flavor of $s_{\pm }$, where the two concentric Fermi surfaces around each ( $\pm \pi$, $\pm \pi$) point carry order parameters of the opposite sign. Such a state would be very similar to an exotic superconducting state proposed for ${\text{YBa}}_2{\text{Cu}}_3{\text{O}}_7$ by Scalapino and by others about $20$ years ago [14], in which the bonding and antibonding concentric Fermi surfaces had opposite signs of the order parameter.

There are other recent experimental reports on this material that would make any superconductivity expert cringe. Several papers, among them neutron scattering studies [15], Mössbauer [16], and $\mu$SR [17] spectroscopy, report coexistence of superconductivity and very strong antiferromagnetism. Magnetic moments up to $3.3{\mu }_B$ per $\text{Fe}$ atom have been observed. Note that the exchange fields associated with such large magnetic moments are of the order of $40,000$ Tesla. Any incomplete compensation of these fields, such as that resulting from a net canting of the order of $0.05$ degree, would have created a net field larger than the critical field $H_{c2}$. The crucial question, addressed to NMR spectroscopists, is as follows: Do superconductivity and magnetism coexist on a microscopic scale? If the answer comes in the affirmative, then we are facing a real mystery, to which the questions of the pairing symmetry and the pairing mechanism pale in comparison. As this article is being written, the reports are contradictory. Some claim that superconductivity occurs only in the charge-balanced compositions with the general formula ${\text{K}}_x{\text{Fe}}_{2-x/2}{\text{Se}}_2$, and only when $\text{Fe}$ vacancies (see below) are ordered and magnetism sets in [18]. Others insist that superconductivity only occurs in samples where vacancies are disordered, and that superconductivity and magnetism occur in the same samples, but never simultaneously [19].

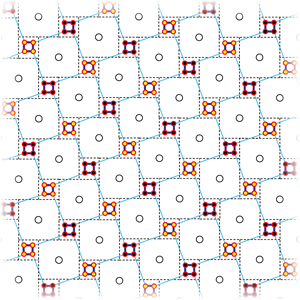
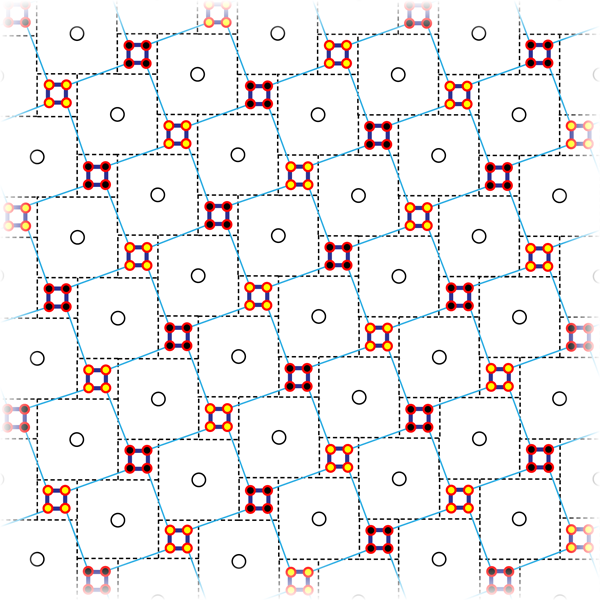
This magnetic state, whether or not it coexists with superconductivity at a microscopic level, is very intriguing in itself. Neutron scattering experiments indicate that magnetism occurs in iron-deficient samples when the associated vacancies form an order $\sqrt{5}\times \sqrt{5}$ superstructure [13] that can be viewed as an assembly of ${\text{Fe}}_4$ square plaquettes connected at their corners (see Fig. 2). Neutron spectroscopy detects parallel spins at each plaquette [13], thus making their combined moment about $13{\mu }_B$. These supermoments then order to form a checkerboard. This ordered structure corresponds to a chemical formula ${\text{K}}_2{\text{Fe}}_4{\text{Se}}_5$, or ${\text{K}}_{0.8}{\text{Fe}}_{1.6}{\text{Se}}_2$, using a more familiar notation. Interestingly, density functional calculations reproduce this result, and give more insight into it [20]. It appears that iron-iron bonds inside the plaquettes are shorter than those between them (Fig. 2), and this is not a magnetoelastic effect: the calculations predict such a bond contraction even without spin polarization. With the large iron moment also reproduced, the calculated antiferromagnetic state is, most interestingly, a band insulator. In the experiment, the nominal composition ${\text{K}}_{0.8}{\text{Fe}}_{1.6}{\text{Se}}_2$ is metallic. However, nearby in the phase diagram, an insulating phase does appear. Early publications identify this phase as a Mott insulator, but in view of these calculations it will more likely prove to be a band insulator.

Credit: Alan Stonebraker

Credit: Alan Stonebraker

×

The issue of stoichiometry as well as the exact chemical composition and homogeneity of the material are of utmost importance. Indeed, bulk probes, such as neutrons, universally give compositions with pronounced iron deficiency [13,16]. It was suggested, based on these data and on the first-principles calculations [18], that the superconducting samples are always “charge balanced,” i.e., they have the chemical formula ${\text{K}}_x{\text{Fe}}_{2-x/2}{\text{Se}}_2$. Iron in this formula has the same valence ( $+2$) as in pnictide superconductors or in $\text{FeSe,}$ and, in a nonmagnetic disordered state should have a similar semimetallic band structure favorable for $s_{\pm }$ pairing. However, ARPES data [9], which are sometimes measured on the same samples, suggest a much more doped composition, in fact closer to the ${\text{KFe}}_2{\text{Se}}_{2}1/2/2$ stoichiometry. One possibility is that, for some as yet unknown reason, vacancies form only in the bulk but not on the surface. In that case, the bulk electronic structure (forgetting for a moment about the existing magnetic order) should be the same as in the other pnictides, with all the glory of the $s_{\pm }$ model recovered. The surface would then be strongly electron doped, compared to the bulk, so that the hole bands at the surface disappear, but superconductivity is retained by virtue of the proximity effect to the bulk.

To conclude, these recently discovered systems open an entirely new universe in the world of iron-based superconductors. There are good reasons to suspect that these new materials will turn out to be qualitatively different from the “old” iron-based superconductors. It may also happen that as the experiments improve, the number of mysteries will diminish, and the “new” materials will appear closer to the “old” ones. However, this is arguably the most interesting development in the field since the original discovery.