In tight spaces

Toshio Hyodo

Viewpoint

In tight spaces

Slow Positron Facility, Institute of Materials Structure Science, High Energy Accelerator Organization, KEK, 1-1 Oho, Tsukuba, Ibaraki 305-0801, Japan

January 10, 2011• Physics 4, 3

Laser spectroscopy of positronium confined to nanoscale pores is a tool to probe the size of buried cavities and a step toward the long-term goal of a positronium BEC.

Figure caption — **Figure 1:** Two experimental setups allow Cassidy *et al.* to measure and compare the excitation spectra of “free” and confined positronium. (Top plot) The excitation spectrum of positronium that escapes the sample surface is measured using laser light aimed parallel to the sample surface (top right schematic). By rotating the sample $45$ degrees (bottom right schematic), it is possible to probe $Ps$ that lies within the silica pores as well as the $Ps$ outside (bottom plot). The spectrum has two components: one shifted to longer wavelength (free $Ps$ , in vacuum) and the other shifted to shorter wavelength (cavity $Ps$ , inside the pores).

Positronium ( $Ps$ ) is the bound state of an electron and its antiparticle, the positron [1]. It is made purely of leptons and, as such, provides a unique opportunity for studying bound-state, two-body quantum electrodynamics and the effect of virtual annihilation that occurs between a particle and an antiparticle in a bound state.

So far, experimentalists performing precision measurements [2] of the energy levels and the intrinsic lifetime of $Ps$ have made every effort to eliminate the effects of the environment so they could compare their results with theoretical predictions [3]. In a paper appearing in Physical Review Letters, David Cassidy and colleagues at the University of California, Riverside, and San Diego State University present a spectroscopic study of the $Ps$ atom in a completely different situation [4]. They measure the line shape of the Lyman- $α$ atomic transition (the $1 S$ - $2 P$ transition) of $Ps$ confined within the roughly $5 nm$ diameter pores of a porous silica film. This is the first time that spectroscopy has been done on atoms inside such small pores, and shows that the $1 S$ - $2 P$ transition energy of $Ps$ confined to the nanometer length scale is significantly shifted compared to “free” $Ps$ . One of the long-term goals of studying $Ps$ in confinement is to produce a positronium Bose-Einstein condensate (BEC). With positronium’s small mass (and long de Brogli wavelength), it should be possible to form a $Ps$ BEC at higher temperatures than with more massive atoms like sodium or rubidium [5]. There are, of course, obvious difficulties in doing this, which stem from the complexities of preparing antiparticles and cooling them within their short lifetime of $140 ns$ . In this context, Cassidy et al.’s results are an important proof of principle that optical spectroscopy of the confined $Ps$ atoms can be made before they annihilate.

Silica is well known as a medium for forming $Ps$ . Positrons shot into a silica target can, as they thermalize, interact with electrons in the solid to form $Ps$ . If the target is porous silica, an aggregate of silica nanoparticles, or ultrafine silica powders, the $Ps$ atoms are likely to diffuse to a surface from which they can be spontaneously emitted into the pore region or free space between the nanoparticles. (Similarly, some of the positrons that diffuse to the surface may also form $Ps$ by picking up an electron.) Once within these “voids,” a $Ps$ atom will not return to the bulk. This is because the work function of $Ps$ for silica is negative, meaning that it costs more energy for the $Ps$ atom to be in the silica than in the vacuum [6]. Perhaps it is worth mentioning that the particle-antiparticle annihilation is a relatively slow process compared to electron and phonon excitations and $Ps$ formation.

$Ps$ is unique among the neutral atoms in that it spontaneously emits gamma rays when it annihilates. Analyzing these gamma rays provides a useful probe of a positronium atom’s interaction with other atoms, molecules, or solid surfaces before it annhilates and is an established technique for studying materials. As a result, there are a number of methods for preparing and measuring $Ps$ that consist essentially of detecting the annihilation gamma rays. But in order to perform accurate spectroscopy of $Ps$ in confinement, Cassidy et al. had to first create a very short and dense pulse of positrons to maximize the temporal and spatial overlap of the $Ps$ bunch and the laser beam used in the measurements. Harnessing a series of existing techniques, they first moderated and trapped positrons that were produced by a sodium- $22$ radioactive source in a so-called Surko trap [7]. They then “dumped” the trapped positrons by applying a parabolic potential along the cavity of the trap to form a pulse with a temporal width of $15$ – $20 ns$ , which was further compressed (with a “buncher”) into a subnanosecond pulse containing $\sim 2 \times 10^{7}$ positrons. The pulse was also spatially compressed with a pulsed magnet [8]. Finally, they injected the positron pulse onto a porous silica target having an open pore structure. The lifetime of the ortho- $Ps$ ( $Ps$ with the electron and positron spins parallel) in the pore is shorter than its intrinsic lifetime but still longer than about $50 ns$ , allowing some of the $Ps$ atoms to diffuse though the connected pores into the open space in front of the film surface.

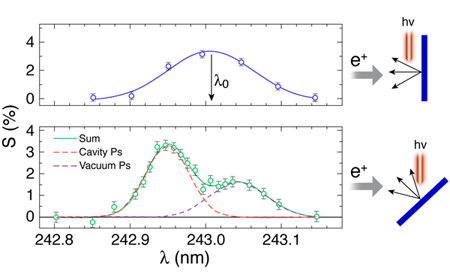
The team used a combination of different lasers and specialty optics to both produce light over a range of frequencies near the $Ps$ Lyman- $α$ transition and to photoionize the $2 P$ state of $Ps$ . They irradiated the target in two configurations: one where the target surface was perpendicular to the positron beam but parallel to the laser light, and a second where the surface was rotated by $\sim 45$ ° with respect to the positron beam and the light axes (see schematics, Fig. 1). In the former case, the light did not touch the surface and thus only the $Ps$ coming out of the surface (vacuum $Ps$ ) was excited. In the latter, the laser entered the silica and the $Ps$ could be excited while inside the film pore.

To make their principle measurement, the team used a technique they developed in earlier work [9], called single-shot positron annihilation lifetime spectroscopy, which yields the excitation spectrum of $Ps$ . When only those $Ps$ atoms that were in the vacuum were excited, they observed a Doppler broadened line shape centered at the $1 S$ - $2 P$ wavelength $λ_{0}$ (top plot, Fig. 1). The broadening occurs because the $Ps$ atoms are moving with a distribution of speeds. When the target was rotated so that the light passed though the film, they saw two components in the line shape, whose centers were above and below $λ_{0}$ (bottom plot, Fig. 1). The longer wavelength component corresponds to free $Ps$ in vacuum: the Doppler broadened line shape is shifted to lower frequencies because the $Ps$ emitted from the tilted target surface is, on an average, moving towards the laser. The shorter wavelength component is due to the transition of $Ps$ atoms inside the pore. The width of this component is narrower than the vacuum component.

Cassidy et al. see an energy shift of about $1.3 meV$ for the confined $Ps$ , which they attribute to energy level shifts of both the $1 S$ and the $2 P$ states. A simple model for the center-of-mass energy level shift that would correspond to changes in the size of the $1 S$ and $2 P$ $Ps$ atoms in confinement would give $Δ E_{0} = 3.6 meV$ , almost three times larger than the observed value. By accounting for the repulsive potential the cavity surface exerts on the $Ps$ wave function [10], they show the shift they observe corresponds to a cavity diameter of $\sim 5 nm$ , consistent with the nominal size of the pore of the sample.

The transition width for positronium in confinement is, experimentally, narrower than that of vacuum, but still broader than expected [11]. That said, the line shapes for “free” $Ps$ are already extremely broad because of positronium’s low mass; thus any methods to further narrow them would open up the possibility of, for example, using positronium atoms for gravity interferometry experiments [12]. Since Cassidy et al. attribute the residual broadening they see to disorder in the sample, it may be possible to achieve narrower $Ps$ transitions by using a sample with less disorder.

The fact that Cassidy et al. are able to perform laser spectroscopy of confined positronium before the atoms annihilate provides a new method for the determination of the size of pores in materials in addition to the already established uses of $Ps$ [13]. It also paves the way for preparing a $Ps$ BEC. Though challenges remain, including finding a way to increase the spatial density of the injected positrons and to effectively cool the $Ps$ atoms, a $Ps$ BEC could be the ultimate source for precision measurements. Though it is an even longer-term goal, there is particular interest in observing stimulated annihilation from a positronium BEC as a first step toward making a gamma-ray laser.

References

A. Rich, Rev. Mod. Phys. 53, 127 (1981)
For example, M. S. Fee, et al., Phys. Rev. A 48, 192 (1993); R. S. Vallery, P. W. Zitzewitz, and D. W. Gidley, Phys. Rev. Lett. 90, 203402 (2003); O. Jinnouchi, S. Asai, and T. Kobayashi, Phys. Lett. B 572, 117 (2003)
S. Adkins et al., Ann. Phys. (N.Y.) 295, 136 (2002), and references therein.
D. B. Cassidy, M. J. Bromley, L. C. Cota, T. H. Hisakado, H. W. K. Tom, and A. P. Mills, Phys. Rev. Lett. 106, 023401 (2011)
B. Cassidy and J. A. Golovchenko, in New Directions in Antimatter Chemistry and Physics, edited by C. M. Surko and F. A.Gianturco (Kluwer Academic, Dordrecht, 2001)[Amazon][WorldCat]; P. M. Platzman and A. P. Mills, Jr., Phys. Rev. B 49, 454 (1994)
Y. Nagashima et al., Phys. Rev. B 58, 12676 (1998)
C. M. Surko and R. G. Greaves, Phys. Plasma 11, 2333 (2004)
D. B. Cassidy et al., Rev. Sci. Instrum. 77, 073106 (2006)
D. B. Cassidy et al., Appl. Phys. Lett. 88 194105 (2006)
J. Mitroy and G. G. Ryzhikh, J. Phys. B 32, 2831 (1999); V. A. Dzuba et al., Phys. Rev. A 60 3641 (1999)
R. H. Dicke, Phys. Rev. 89, 472 (1953); T. Ido and H. Katori, Phys. Rev. Lett. 91, 053001 (2003)
A. Kellerbauer et al., Nucl. Instrum. Methods B 266, 351 (2008); A. P. Mills, Jr., and M. Leventhal, Nucl. Instrum. Meth. B 192, 102 (2002)
S. J. Tao, J. Chem. Phys. 56, 5499 (1971); M. Eldrup et al., Chem. Phys. 63, 51 (1981); M. Hasegawa et al., Nucl. Instrum. Meth. B 91, 263 (1994)

About the Author

Toshio Hyodo is a Professor at the Institute of Material Structure Science, High Energy Accelerator Research Organization and a Professor Emeritus at the University of Tokyo. He is ex-Chair of the International Advisory Committee on Positron Annihilation and the current President of the Japanese Positron Science Society. He received his Ph.D. from the University of Tokyo in 1979 for his experimental work on positron annihilation in solids. During 1980–1982 he was a visiting researcher at the Physics Department of Queen’s University, Canada. His research interests include positronium ( $Ps$ ) states in solid materials and $Ps$ interactions with molecules and solid surfaces using silica aerogel as a $Ps$ formation medium, as well as slow positron beam instrumentations. He is also actively interested in the improvement of physics education.