Trend

Does cell biology need physicists?

    Charles W. Wolgemuth
    • University of Connecticut Health Center, Department of Cell Biology and Center for Cell Analysis and Modeling, Farmington, CT 06030-3505, USA
• Physics 4, 4
Allured by the chic perception and higher funding levels of disease-oriented research, many physicists have migrated to cell biology. Does physics really play a dominant role, or is cellular physiology slave to genetics and chemistry?
Introduction

Cells are the fundamental units of life. At a basic level, a cell’s primary functions are to grow, replicate, and divide. Survival, at least for a sufficient length of time, is also extremely important in order to achieve these other functions. However, as humans, we want more. We don’t only want our cells to provide us with a sufficient length of life that we can reproduce; we would also like to guarantee ourselves a long and healthy existence. These desires, though, are all too often thwarted by disease. Though diseases can be caused by a number of different factors, such as molecular toxins, acquired or inherited genetic defects, viruses, and bacteria, which all act at different scales (molecular, cellular, and even multicellular), in most cases, disease represents a cellular level process; i.e., most diseases are, at their heart, a disruption of cellular function, which then ultimately produces organ or organism disability or failure.

Since humans would prefer to live a disease-free existence, it is not surprising that biological and health-related research is highly respected or that the National Institutes of Health have deeper pockets than the National Science Foundation. In addition, recent technological advances have allowed us to look at molecules and cells in much more detail. We are now able to resolve and quantify, at subcellular and even molecular levels, the spatiotemporal dynamics of molecules and processes inside cells. Therefore molecular and cellular biology have become more amenable to a research paradigm that melds experimental and theoretical investigations, and, more specifically, research that is geared toward an accurate description of how things move in space and time. It is, therefore, not surprising that physicists would be attracted to cell biological research.

But the past has shown that cell biologists are extremely capable of making great progress without much need for physicists (other than needing physicists and engineers to develop many of the technologies that they use). Do the new data and new technological capabilities require a physicist’s viewpoint to analyze the mechanisms of the cell? Is physics of use to cell biology?

The elephants in the room: genetics, proteomics, and systems biology

It is hard to overestimate the role that genetics has played in biology over the last 30 years. Molecular and cellular biology, to a very large extent, are about proteins and their interactions. The ability to perturb a specific protein inside a cell and then observe the consequences has led to an amazing number of advances in our understanding of the roles of certain proteins in cellular function. It would almost seem that if we could just compile a list of all the proteins inside the cell (a field called proteomics) and determine their reactions and reaction rates, we would understand how a cell works. With high-throughput methods, we are now able to quickly measure DNA transcripts and protein levels and correlate these with observed cell characteristics (“phenotypes”) [1]. We have amassed a lot of data, and the more we put together, the more complex and harder to interpret the data becomes.

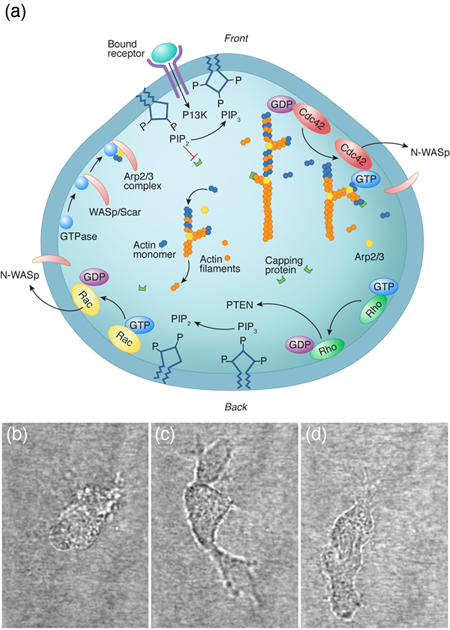
For a cell with a fairly small genome, such as the yeast Saccharomyces cerevisiae, which can produce between 104 and 105 proteins, the number of possible protein interactions is 105– 107 [1]. Even if we consider a single cellular function (for instance, the ability of a eukaryotic cell to move along a substrate) the chemical reaction network that describes this behavior appears incomprehensible (Fig. 1). The hope of systems biology is to use a higher level approach to understand these systems, to analyze the reaction networks at a more functional level and provide a framework for assembling models of biological pathways from systematic measurements [2]. Absent from this discussion is any mention of the physics involved in cellular processes. It is possible that the physics that cells must deal with is slave to the reactions; i.e., the protein levels and kinetics of the biochemical reactions determine the behavior of the system, and any physical processes that a cell must accomplish are purely consequences of the biochemistry. Or, could it be that cellular biology cannot be fully understood without physics?

Credit: Carin Cain
Figure 1: The complexity of cellular biology. (a) A subset of the chemical reactions that drive eukaryotic cell crawling. In brief, cells sense the environment through membrane bound proteins. Activation of these receptors leads to activation of a number of other proteins that promote the polymerization of actin. The biochemical reactions that govern the dynamics of actin are included. These chemical reactions produce cell motility. (b)–(d) Time series of a cancer cell (HT1080 fibrosarcoma cell) moving through a collagen I matrix. There are two hour intervals between each frame. (Images courtesy of D. Wirtz, Johns Hopkins University.)
Some examples of successful physical biology

The successes of genetics and biochemistry in describing cellular function have overshadowed an important point: Cells are not isolated bags of proteins. The inside of a cell has structure, and this structure is not static. In addition, cells must live in and interact with the environment, which is often unpredictable and not always favorable. In order to grow, move, and survive, cells must be able to produce force. That is, physics matters, at least at some level.

Molecular motors

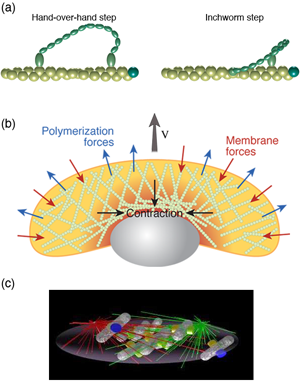
Inside cells there are proteins that convert chemical energy into useful work. For example, kinesins and dyneins haul cargo around the cell. Myosin molecules can bind to actin filaments and exert forces, which is how our muscles work. Other molecules rotate, such as the protein that creates the molecules that are the prime fuel of our cells. The general method by which these molecular motors operate is through a Brownian ratchet mechanism [3]. However, whereas the classic Brownian ratchet does not actually work, molecular motors harness molecular binding energies to satisfy the second law of thermodynamics. Typically, binding of an ion or molecule (such as ATP) to the motor leads to a conformational change in the protein. This conformational change can act like a power-stroke in the motor. Hydrolysis of ATP or release of the bound ion then returns the motor to its original state, thereby completing a cycle (or, in the case of rotational motors, a binding and release event typically only produces a substep of a complete rotation).

Since these molecules act like motors, the best way to characterize them is through their force velocity relationship. Optical trapping methods and other biophysical experiments have provided quantitative information in regard to the force velocity relationship for many of these motors, such as kinesin [4], myosin [5] [Fig. 2 (a)], the bacterial flagellar motor [6], and the bacteriophage portal motor, which packages DNA into the virus [7]. These experiments along with other biophysical measurements of molecular motors, as well as structural information on the proteins, allow us to conceive of possible ways that these motors can function. Then, using modeling, we can test these hypotheses to determine whether the proposed mechanism could work, which has lead to a clear picture of the function of myosin [8], kinesin [9], ATP synthase [10], and the flagellar motor [11]. Dynein, however, remains perplexing [12]. Interestingly, combining the results of these types of models and experiments with a more macroscopic view has lead to a model that captures the behavior of muscle [13].

Credit: Carin Cain
Figure 2: Some examples where physics has shed light on biology. (a) Physics-based simulations of the walking of myosin VI predicted that the molecule would produce both hand-over-hand and inchworm type movements [8], which was later confirmed with single molecule experiments [57]. (Image courtesy of S. X. Sun, Johns Hopkins University.) (b) A crawling cell is driven primarily by the dynamics of its actin cytoskeleton, a network of filaments that polymerize at the leading edge of the cell. Force balance on the crawling cell comes from membrane forces (tension and bending), a polymerization forces, and contractile forces generated inside the cell by myosin motors and other unknown mechanisms. Here we depict a fish keratocyte, which crawls at a roughly constant speed V, while maintaining a steady cell shape. The cell body is shown in gray. (c) Stochastic simulations of microtubules determined some of the constraints for the accurate and efficient capturing of chromosomes during the formation of the mitotic spindle. (Image courtesy of A. Mogilner, University of California, Davis.)
Cellular movement

Another obvious and accepted role of physics in cell biology has been in understanding the motion of cells or in determining the mechanisms by which cells move (both of which are lumped under the heading cell motility). The number of different ways that cells have figured out how to move is astounding. They can crawl, glide, swim, and twitch. And, for each of these types of motility, there are many different mechanisms that achieve the same end.

Many animal cells, including metastatic cancer cells, white blood cells, and the skin cells that assist with healing wounds, crawl. The general process has been shown to require polymerization of filamentous actin at the front of the cell, adhesion to the surrounding environment, and a contractile mechanism that produces the force required to haul the rest of the cell forward. Physicists have generated and are still producing an informative description of all three of these processes. For example, the actin polymerization that produces the force that pushes out the front of the cell is another Brownian ratchet mechanism [14]. Adhesion to the substrate is mediated by proteins that span the cell membrane and can bind (indirectly) to actin. While these interactions have often been treated as rigid links between the cytoskeleton and the environment, theoretical considerations of the biochemistry and force dependence of adhesion proteins actually suggest that the resulting adhesive force behaves more like a viscous drag force than like a rigid attachment [15,16]. Originally, the contraction that drives the rear of the cell was believed to come from acto-myosin, as in muscle [17]. However, myosin is most likely not the only mechanism at play. Other mechanisms that have been proposed include chemically-induced contraction and unbundling or depolymerization of the cytoskeleton [18]. It is now possible to test theoretically the behavior of these mechanisms using whole cell simulations. By comparing the predictions of models such as these to experiments, it may soon be possible to determine how cells pull themselves forward.

How cells swim

In most instances, swimming is driven by the active motion of filamentary objects. Bacteria and Archaebacteria typically rotate long, thin, helical filaments using a molecular rotary motor that is driven by ionic flux. The motor is attached at one end of the filament and anchored into the inner membrane of the cell. Eukaryotic swimmers, on the other hand, utilize filaments that undulate or rotate, driven by dynein motors and are distributed along the length of the filament. G. I. Taylor and Edward Purcell were the first to consider the fluid mechanical principles that allow microorganisms to move through viscous fluids. Motivated by their work, Howard Berg was one of the pioneers of quantitative biophysical investigations of the swimming of bacteria and showed that Escherichia coli swims by a series of runs and tumbles, allowing bacteria to use a random walk to move through the environment, while others were showing the role of the bacterial flagellum in motility [6]. Similarly, Charles Brokaw and co-workers were carrying out quantitative investigations of the swimming of mammalian sperm [19]. The field of microorganism swimming has remained an active field for physical biologists. In recent years, work has focused on a number of interesting topics, such as the optimization of different low Reynolds number swimming strokes [20–22] and the effects of swimming near surfaces [23–25]. Chlamydomonas was recently shown to use a run and tumble swimming mechanism that may be driven by the noisy oscillations of its flagella [26,27]. Two areas that are beginning to receive a lot of attention are collective swimming [28] and swimming in non-Newtonian environments [29–33]. The former describes the seemingly organized or sometimes turbulent behavior that naturally arises when groups of cells are swimming near one another. But of all the recent work on swimming, the behavior of swimmers in non-Newtonian environments may be the most relevant for human health and disease. For example, sperm cells must navigate through viscoelastic cervical fluid [34,35], and invading bacteria must maneuver through the collagen filament networks of our skin, penetrate through layers of cells [36], and move through the mucus in our stomachs [37].

Cell growth and division

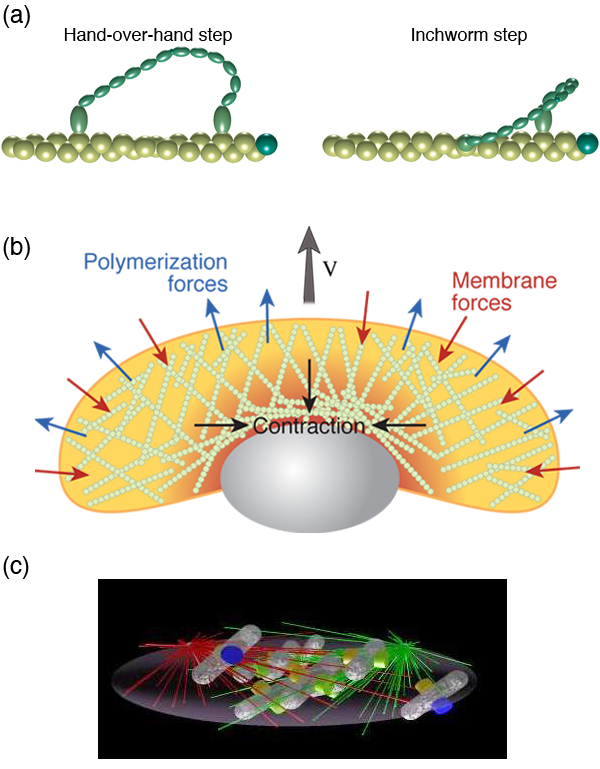
To divide, cells must separate the copies of their DNA and pinch the mother cell into two daughters. The process of separating the chromosomes in eukaryotes is driven by a spindle of microtubules. Though a wealth of experimental data exists on this process, an understanding of the self-assembly and mechanics of the process is lacking. Stochastic simulations have recently revealed some of the possible processes involved in the formation of the spindle [38] [Fig. 2 (c)], and a mechanical model has shown the force balance involved in determining spindle shape [39]. How bacteria partition the copies of the genome, though, is less clear [40]. To constrict the cell during division, bacteria and eukaryotic cells use a dynamic ring of proteins. In eukaryotes, the constriction of the ring is believed to be driven by myosin, and consequently, not much modeling of the cytokinetic ring has been done. In bacteria, however, it appears that a motor protein like myosin may not be involved, and physicists have considered other mechanisms, such as condensation of the ring proteins [41] and subunit conformational changes [42], as driving forces for constriction. Until recently, little attention was paid to the physical mechanisms by which cells grow. With the discovery that bacterial shape is tightly controlled, physicists have begun to think about what physics governs growth and cell shape [43–45]. This field remains in its infancy but is likely to show significant progress in the near future.

How cells interact with the environment

The interaction of cells with the environment is one more area where physics is bound to play a significant role in cell biology. Many crawling cells can sense and respond to the stiffness of the surrounding environment, which is known as mechanosensing. It was noted over 25 years ago that fibroblasts that were plated on glass were more spread and less elongated than fibroblasts grown in three-dimensional collagen matrices, and cells that were grown on square adhesive islands have actin filament bundles that lie along the diagonals of the square cell. More recently, it has been observed that cell proliferation can be affected by substrate stiffness [46–49]. Cell motility is also affected by substrate stiffness. For example, fibroblasts migrate more slowly on stiff substrates than they do on soft ones [50]; however, directed motility is more persistent on stiff substrates than on soft ones [51]. Even more surprising, when fibroblasts encounter a boundary between a hard substrate and a soft one, they behave differently depending on which side of the boundary they started on [51]. Cells on the soft side of the boundary will move into the hard region; whereas cells that are on the hard side of the boundary will either move along the boundary or crawl away from it. Furthermore, cells can actually adjust the stiffness of their cytoskeleton in order to try to match the surrounding environment [52]. These abilities are presumed to play a role in how cells respond when they are in different parts of the body, as tissue stiffness varies in different parts of the body [53]. It is interesting to speculate that organism development may be more driven by mechanical cues than by diffusing chemicals (which is what has been previously proposed). How cells are able to sense and respond to the environment is still unknown [54]; however, a recent theoretical model that couples protein kinetics with applied force may explain some of the process [16].

Potential pitfalls for physicists in biology

Fifteen years ago, around the time that I began working in biophysics, there were very few collaborations between physicists and cell biologists, especially if the physicists were theorists. Theory was, and still is to a good degree, a word that should be avoided in the presence of biologists. Those of us who use math and computers to try to understand how cells work tend to call ourselves modelers instead of theorists. My suspicion is that many of the first physicists and mathematicians who tried to develop models for how biology works attempted to be too abstract or too general. As physicists we like to try to find universal laws, and though there are undoubtedly general principles at play in cell biology, it is likely that there are no real universal rules. Evolution need not find only one way to do something but more often probably finds many. Rather than search out generalities, we will serve biology better if we deal with specifics. As Aharon Katchalsky, who is largely credited with bringing nonequilibrium thermodynamics to biology, purportedly said, “It is easier to make a theory of everything than a theory of something.”

In recent years, physicists have done a much better job at addressing specific problems in biology. However, there still remains a divide between the two communities. Indeed, good physical biology that comes out of the physics community often goes unnoticed or is under appreciated. The burden falls on us to properly convey our work so as to be accessible to biologists. We need to make conscious efforts at communication and dissemination of our results. Two useful approaches toward this end are to publish in broader audience journals that reach both communities, and for papers that contain theoretical analyses to provide a qualitative description of the modeling in the main text, while leaving the more mathematical details for the appendices or supplemental material (for further discussion of this topic, see Ref. [55]). It is also of prime importance to maintain and to forge new connections between physicists and biologists.

There is one other concern that I harbor; I worry about the misconceived equating of successful computer simulations and understanding. Over the past 30 years, the computational power that one has at one’s fingertips has increased by orders of magnitude. We are now able to simulate hundreds of coupled ODEs describing large biochemical networks. We can solve these in two and three dimensions with arbitrary transport mechanisms. We can also reproduce in silico the stochastic dynamics of thousands of interacting proteins. We get closer and closer to having the ability to simulate, molecule by molecule, a reasonable fraction of a cell. But then I reflect on the modest advances that these investigations have made in our understanding of how cells work. It seems that Turing may have moved us farther forward with his analytic analysis of reaction-diffusion systems than we have moved since. It would almost seem that there is little or no correlation between computer power and true scientific advancement.

Visions of the future

Though I do not know in which directions biophysics will head, my current impression is that physicists will have the most success by trying to provide a simpler view of the astounding complexity that we see in cellular biology. In the end, the massive interconnected biochemical networks have developed to achieve a countable number of functions, and on top of this, some of the complexity is redundant, a means for self-preservation in the face of mutation and a harsh environment. It therefore may be useful to focus our attention at the level of the functions rather than at the level of the proteins. Reductionism is not always useful. Physicists have done very well with determining what details are important and which aren’t.

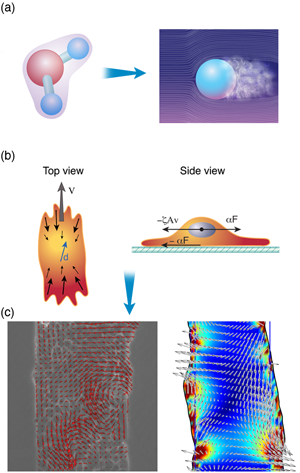
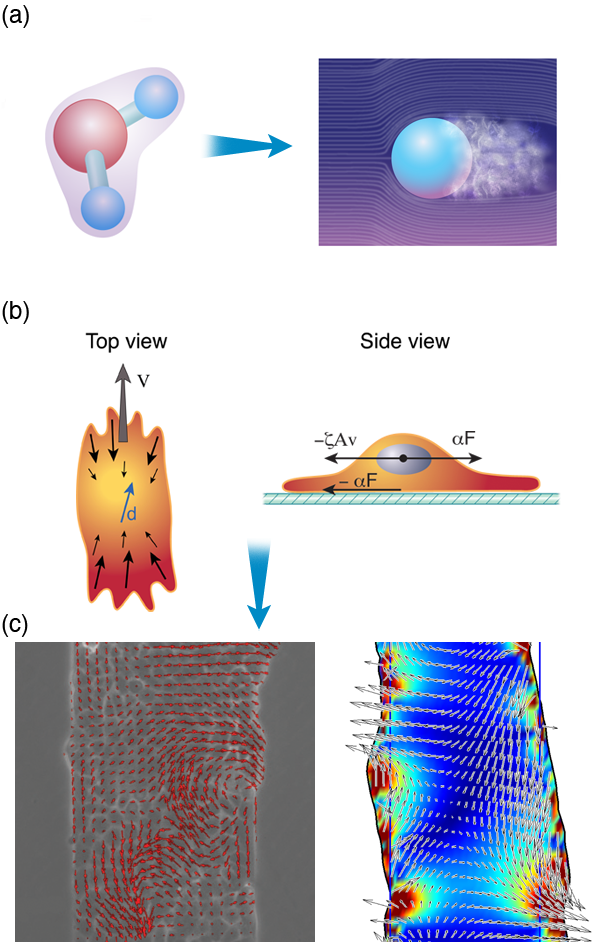
There are at least two means by which this can be done. The first is to examine a high-level behavior and extrapolate general principles. Take, for example, the classic story of Newton, whereby the law of gravity was intuited by the falling of an apple. Whether the story is true or not, Newton was able to determine general laws for understanding macroscopic behavior (as long as the macroscopic object is not moving too fast). The details of quantum mechanics and the intermolecular forces between atoms do not really matter for describing the flight of the baseball on its route from the pitcher’s hand to the awaiting bat; the interaction between the ball and the air matter much more. And now consider this mass of air that surrounds the traveling ball [Fig. 3 (a)]. Once again, the details of the molecular interactions, or even the identities of the molecular constituents of the air, do not matter so much. Between statistical mechanics and fluid mechanics, we can gain a much better description of the bulk behavior of the air than we could if we considered the air at a more fundamental level. Indeed, at the level of a fluid, the molecular details average together into a much smaller set of bulk material parameters, such as the viscosity or the coefficient of thermal expansion. It is these bulk parameters that determine the course of the flying baseball.

Credit: Carin Cain
Figure 3: How physicists may be most useful for cell biology. (a) The cloud of electrons around a water molecule leads to a complex interaction potential between two water molecules (based on Ref. [58]). When we consider the bulk flow of a fluid around a ball, though, these complex interactions lead to a single bulk viscosity, which can be used to accurately calculate the fluid flows about the ball and the resistive force exerted on the ball. (b) In a similar fashion, it is possible to consider the stresses that are created inside a cell due to the dynamics of actin, without worrying about the complex reactions that create this dynamics (as depicted in Fig. 1). Combining this average dipole stress of a single cell and the adhesive interactions between neighboring cells can accurately describe the collective behavior of cells during wound healing. The bottom left panel shows the cellular flows that accompany wound healing (originally published in Ref. [56] and reprinted with permission from P. Silberzan) and a simulation from Lee and Wolgemuth (unpublished data).

As an example, Pilhwa Lee and I have recently been working on a model to describe the physics that is involved in wound healing. When an organism is wounded, epithelial cells crawl to fill in the wounded area. An experimental method for exploring this process is to grow a monolayer of epithelial cells on a substrate and then to “wound” the layer using a scalpel or some other object to scrape away a region of cells. Pascal Silberzan and co-workers have shown that the motion of the cells during wound healing is not trivial and involves long-range order and complex cellular flows [56]. Based on these observations and an analogy between crawling cells and the collective swimming of bacteria, we proposed a model that captures many features that are observed in wound healing assays. We suggest that two dominant physical attributes are responsible for most of the processes involved in wound healing: (i) the dipole nature of the stress distribution of a crawling cell and (ii) cell-cell adhesions. This model absorbs all of the complex biochemistry and actin dynamics inside a cell into two parameters that describe the stress that a cell exerts on its surroundings, and cell-cell adhesion dynamics can be shown to lead to visco-elastic couplings between cells [Fig. 3 (b)]. Therefore, where many groups have focused extensively on the complex biochemical interactions inside the cell, at a functional level (i.e., healing of a wound), many of the molecular details may only act to regulate a few bulk physical parameters.

However, for biology, and especially medicine, it will not suffice to just develop nonreductionist theories of cellular function; it will also be necessary to compute the effective parameters of the theories in terms of the actual molecular level interactions. (Yet another task for which physicists are well suited.) The current paradigm of disease treatment is molecule based. We develop drugs that interact with or replace the proteins that our bodies are or aren’t making. We seek out poisons that specifically target cancer cells. Alzheimer’s patients are treated with molecules that prevent the breakdown of acetylcholine, a chemical implicated in learning and memory. And, some diseases, such as cystic fibrosis, can even be treated by replacing defective genes in an individual with a functional copy of the gene. In addition, biological research is strongly tied to the genetic approach. A specific protein is knocked out, up-regulated, or down-regulated and the resulting phenotype is determined. To be truly successful, we must provide an understanding of biology that spans the gorge from biochemistry and genetics to cellular function, and do it in such a way that our models and experiments are not only informative about physics, but directly impact biology.

Cell biology is awaiting these descriptions. And it may be that physicists are the most able to draw these connections between the protein level description of cellular biology that currently dominates and a more intuitive, yet still quantitative, description of the behavior of cells and their responses to their environments.

Acknowledgments

The author would like to thank S. X. Sun, G. Huber, and I. Moraru for useful discussions.

References

  1. R. C. Jansen, Nat. Rev. Genetics 4, 145 (2003)
  2. H.-Y. Chuang, M. Hofree, and T. Ideker, Annu. Rev. Cell Develop. Biol. 26, 721 (2010)
  3. R. P. Feynman, The Feynman Lectures on Physics (Addison-Wesley, Massachusetts, 1963)[Amazon][WorldCat]
  4. G. Woehlke and M. Schliwa, Nat. Rev. Mol. Cell Biol. 1, 50 (2000)
  5. S. J. Holohan and S. B. Marston, IEE Proc. Nanobiotechnol. 152, 113 (2005)
  6. H. C. Berg, Annu. Rev. Biochem. 72, 19 (2003)
  7. D. E. Smith et al., Nature 413, 748 (2001)
  8. G. Lan and S. X. Sun, Biophys. J. 91, 4002 (2006)
  9. P. J. Atzberger and C. S. Peskin, Bull. Math. Biol. 68, 131 (2006)
  10. G. Oster, H. Wang, and M. Grabe, Phil. Trans. R. Soc. London B 355, 523 (2000)
  11. J. Xing et al., Proc. Natl. Acad. Sci USA 103, 1260 (2006)
  12. S. L. Reck-Peterson et al., Cell 126, 335 (2006)
  13. G. Lan and S. X. Sun, Biophys. J. 88, 4107 (2005)
  14. A. Mogilner and G. Oster, Biophys. J. 84, 1591 (2003)
  15. S. Leibler and D. A. Huse, J. Cell Biol. 121, 1357 (1993)
  16. S. Walcott and S. X. Sun, Proc. Natl. Acad. Sci. USA 107, 7757 (2010)
  17. H. E. Huxley, Nature 243, 445 (1973)
  18. A. Mogilner, J. Math. Biol. 58, 105 (2009)
  19. C. J. Brokaw, J. Exp. Biol. 43, 155 (1965)
  20. D. Tam and A. E. Hosoi, Phys. Rev. Lett. 98, 068105 (2007)
  21. H. Wada and R. R. Netz, Phys. Rev. Lett. 99, 108102 (2007)
  22. J. Yang, C. W. Wolgemuth, and G. Huber, Phys. Rev. Lett. 102, 218102 (2009)
  23. G. Li, L.-K. Tam, and J. Tang, Proc. Natl. Acad. Sci. USA 105, 18355 (2008)
  24. G. Li and J. Tang, Phys. Rev. Lett. 103, 078101 (2009)
  25. E. Lauga et al., Biophys. J. 90, 400 (2006)
  26. M. Polin et al., Science 325, 487 (2009)
  27. R. E. Goldstein, M. Polin, and I. Tuval, Phys. Rev. Lett. 103, 168103 (2009)
  28. D. L. Koch and G. Subramanian, Annu. Rev. Fluid Mech. 43, 637 (2011)
  29. E. Lauga, Phys. Fluids 19, 083104 (2007)
  30. T. Normand and E. Lauga, Phys. Rev. E 78, 061907 (2008)
  31. H. C. Fu, C. W. Wolgemuth, and T. R. Powers, Phys. Rev. E 78, 041913 (2008)
  32. H. C. Fu, C. W. Wolgemuth, and T. R. Powers, Phys. Fluids 21, 033102 (2009)
  33. J. Teran, L. Fauci, and M. J. Shelley, Phys. Rev. Lett. 104, 038101 (2010)
  34. J. Rutllant, M. Lopez-Bejar, and F. Lopez-Gatius, Reprod. Dom. Animals 40, 79 (2005)
  35. D. P. Wolf et al., Fertil. Steril. 28, 47 (1977)
  36. T. J. Moriarty et al., PLoS Pathogens 4, e1000090 (2008)
  37. J. P. Celli et al., Proc. Natl. Acad. Sci. USA 106, 14321 (2009)
  38. R. Paul et al., Proc. Natl. Acad. Sci. USA 106, 15708 (2009)
  39. B. Rubinstein et al., Phys. Biol. 6, 016005 (2009)
  40. T. Kruse and K. Gerdes, Trends Cell Biol. 15, 343 (2005)
  41. G. Lan et al., Proc. Natl. Acad. Sci. USA 106, 121 (2009)
  42. J. F. Allard and E. N. Cytrynbaum, Proc. Natl. Acad. Sci .USA 106, 145 (2009)
  43. H. Y. Jiang and S. X. Sun, Phys. Rev. Lett. 105, 028101 (2010)
  44. R. Mukhopadhyay and N. S. Wingreen, Phys. Rev. E 80, 062901 (2009)
  45. O. Sliusarenko et al., Proc. Natl. Acad. Sci. USA 107, 10086 (2010)
  46. E. Hadjipanayi, V. Mudera, and R. A. Brown, J. Tissue Eng. Regen. Med. 3, 77 (2008)
  47. J. P. Winer et al., Tissue Eng. Part A 15, 147 (2009)
  48. H. B. Wang, M. Dembo, and Y. L. Wang, Am. Physiol. Cell Physiol. 279, C1345 (2000)
  49. S. X. Hsiong et al., J. Biomed. Mater. Res. A 85, 145 (2008)
  50. R. J. Pelham and Y. Wang, Proc. Natl. Acad. Sci. USA 94, 13661 (1997)
  51. C. M. Lo et al., Biophys. J. 79, 144 (2000)
  52. F. J. Byfield et al., Biophys. J. 96, 5095 (2009)
  53. D. E. Discher, P. A. Janmey, and Y.-L. Wang, Science 310, 1139 (2005)
  54. P. A. Janmey et al., Cell Motil. Cytoskel. 66, 597 (2009)
  55. D. G. Drubin and G. Oster, Mol. Biol. Cell 21, 2099 (2010)
  56. M. Poujade et al., Proc. Natl. Acad. Sci. USA 104, 15988 (2007)
  57. S. Nishikawa et al., Cell 142, 879 (2010)
  58. S. M. Kathmann, I. F. W. Kuo, and C. J. Mundy, J. Am. Chem. Soc. 130, 16556 (2008)

About the Author

Image of Charles W. Wolgemuth

Charles Wolgemuth received his Ph.D. from the University of Arizona in 2000. After a brief stint at the University of California, Berkeley, working with George Oster, he took a faculty position in the Department of Cell Biology and the Richard D. Berlin Center for Cell Analysis and Modeling at the University of Connecticut Health Center, where he has been since. He is currently the Director for the Cell Analysis and Modeling graduate program and an Editorial Board Member for the Biophysical Journal. His research investigates the mechanisms that cells use to move, grow, and to create and maintain their shapes.

Subject Areas

Biological PhysicsInterdisciplinary Physics

Related Articles

Vaccination Strategy Targets Fast-Changing Pathogens
Interdisciplinary Physics

Vaccination Strategy Targets Fast-Changing Pathogens

A theory outlines an immunization protocol that fosters powerful antibodies while avoiding immune-cell death. Read More »

Simulations Suggest Flu Virus Vulnerability
Biological Physics

Simulations Suggest Flu Virus Vulnerability

Studies of influenza A’s unusual propulsion strategy suggest that drugs could target a critical protein. Read More »

Alignment of Cells Affects Secondary Tumor Growth
Soft Matter

Alignment of Cells Affects Secondary Tumor Growth

Cell–cell alignment and a background of stationary cells together shape the emergence of cellular clusters in a primary tumor. Read More »

More Articles